Utilizador:
Capilaridade no tubo na superfície
Definição 
A elevação do menisco ocorre devido ao equilíbrio entre a pressão gerada pela tensão superficial (para cima) e a coluna de água (para baixo).
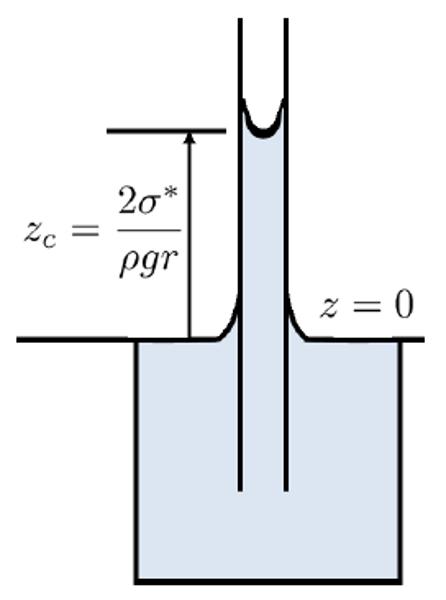
Ao igualar essas duas forças, determina-se a altura da coluna.
ID:(2983, 0)
Capilaridade do tubo
Imagem
Quando um tubo muito estreito é mergulhado em um líquido, como água, observa-se que o menisco se eleva acima do nível da água fora do tubo.
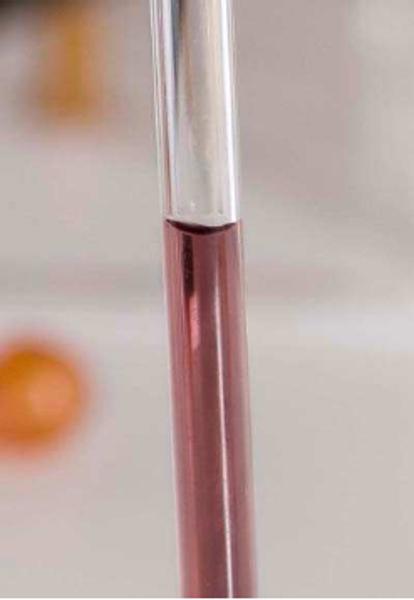
Esse fenômeno é conhecido como capilaridade e é um dos fatores que auxiliam na ascensão da água pelo caule de uma planta.
ID:(2981, 0)
Tensão superficial prática
Nota
Se um anel for pendurado em um dinamômetro, é possível determinar o seu peso.
Ao tentar submergir o anel na água, observa-se que a medida de peso diminui consideravelmente enquanto o anel não consegue penetrar na água. Isso ocorre devido à tensão superficial que impede a penetração da superfície pelo anel. O peso é reduzido pela tensão superficial multiplicada pela área de contato.
Uma vez que o anel penetra na água, o dinamômetro retorna quase ao peso original. No entanto, esse peso é ligeiramente inferior, pois o anel sofre um pouco de sustentação devido à água deslocada.
Ao tentar retirar o anel da água, observa-se que ele pode ser removido facilmente até que a borda inferior do anel atinja a superfície. Neste momento, o anel começa a arrastar a superfície que permanece aderida à borda. A força aumenta progressivamente, pois a área de superfície aumenta. Isso muda abruptamente quando a superfície se rompe e o anel é finalmente liberado.
ID:(117, 0)
Equação da capilaridade do tubo
Citar
A tensão superficial faz com que o menisco se curve, adquirindo um raio $R$, resultando em um ângulo de contato $\theta$ entre a superfície do líquido e a borda:
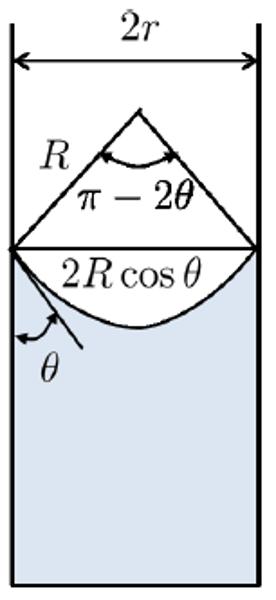
ID:(2982, 0)
Capilaridade
Descrição
Variáveis
Cálculos
para 
,
depois, selecione a variável: 
para 
Cálculos
Variáve
Dado
Calcular
Objetivo :
Equação
A ser usado
Equações
Exemplos
A eleva o do menisco ocorre devido ao equil brio entre a press o gerada pela tens o superficial (para cima) e a coluna de gua (para baixo).
Ao igualar essas duas for as, determina-se a altura da coluna.
(ID 2983)
Quando um tubo muito estreito mergulhado em um l quido, como gua, observa-se que o menisco se eleva acima do n vel da gua fora do tubo.
Esse fen meno conhecido como capilaridade e um dos fatores que auxiliam na ascens o da gua pelo caule de uma planta.
(ID 2981)
Se um anel for pendurado em um dinam metro, poss vel determinar o seu peso.
Ao tentar submergir o anel na gua, observa-se que a medida de peso diminui consideravelmente enquanto o anel n o consegue penetrar na gua. Isso ocorre devido tens o superficial que impede a penetra o da superf cie pelo anel. O peso reduzido pela tens o superficial multiplicada pela rea de contato.
Uma vez que o anel penetra na gua, o dinam metro retorna quase ao peso original. No entanto, esse peso ligeiramente inferior, pois o anel sofre um pouco de sustenta o devido gua deslocada.
Ao tentar retirar o anel da gua, observa-se que ele pode ser removido facilmente at que a borda inferior do anel atinja a superf cie. Neste momento, o anel come a a arrastar a superf cie que permanece aderida borda. A for a aumenta progressivamente, pois a rea de superf cie aumenta. Isso muda abruptamente quando a superf cie se rompe e o anel finalmente liberado.
(ID 117)
A tens o superficial faz com que o menisco se curve, adquirindo um raio $R$, resultando em um ngulo de contato $\theta$ entre a superf cie do l quido e a borda:
(ID 2982)
Se uma superf cie l quida com tens o superficial $\sigma$ apresenta curvatura com raio $r$, a press o gerada na dire o da superf cie dada por
| $ p \equiv\displaystyle\frac{2 \sigma }{ r }$ |
.
(ID 4484)
ID:(881, 0)