User:
Parallel hydraulic elements (3)
Storyboard 
When hydraulic elements are connected in parallel, the flow is distributed among them, while the pressure drop is the same for all of them. The sum of the individual flows results in the total flow, and therefore, the total hydraulic resistance is equal to the inverse of the sum of the inverses of the individual hydraulic resistances. On the other hand, hydraulic conductivities are summed directly.
ID:(2108, 0)
Hydraulic resistance of elements in parallel (3)
Concept
One efficient way to model a tube with varying cross-sections is to divide it into sections with constant radii and then sum the hydraulic resistances in series. Suppose we have a series of elements the hydraulic resistance in a network ($R_{hk}$), whose resistance depends on the viscosity ($\eta$), the cylinder k radio ($R_k$), and the tube k length ($\Delta L_k$), according to the following equation:
| $ R_h =\displaystyle\frac{8 \eta | \Delta L | }{ \pi R ^4}$ |
In each element, we consider a pressure difference in a network ($\Delta p_k$) along with the hydraulic resistance in a network ($R_{hk}$) and the volumetric flow rate the volume flow ($J_V$), where Darcy's law is applied:
| $ \Delta p = R_{h2} J_{V2} $ |
The total resistance of the system, the flujo de Volumen Total ($J_{Vt}$), is equal to the sum of the individual hydraulic resistances volume flow in a network ($J_{Vk}$) of each section:
| $ J_{Vt} =\displaystyle\sum_k J_{Vk} $ |
Thus, we have:
$J_{Vt}=\displaystyle\sum_k \Delta J_{Vk}=\displaystyle\sum_k \displaystyle\frac{\Delta p_k}{R_{hk}}=\left(\displaystyle\sum_k \displaystyle\frac{1}{R_{hk}}\right)\Delta p\equiv \displaystyle\frac{1}{R_{pt}}J_V$
Therefore, the system can be modeled as a single conduit with a total hydraulic resistance calculated by summing the individual components:
| $\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$ |
ID:(15950, 0)
Hydraulic conductance of parallel elements (3)
Concept
In the case of a sum where the elements are connected in series, the total hydraulic conductance of the system is calculated by adding the individual hydraulic conductances of each element.
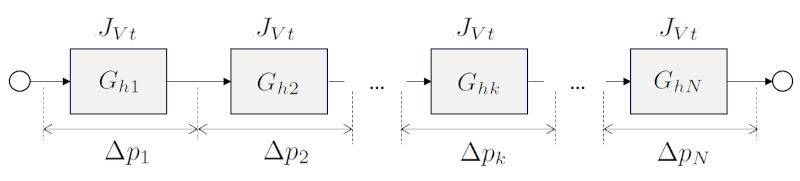
the total hydraulic resistance in parallel ($R_{pt}$), along with the hydraulic resistance in a network ($R_{hk}$), in
| $\displaystyle\frac{1}{ R_{pt} }=\sum_k\displaystyle\frac{1}{ R_{hk} }$ |
and along with the hydraulic conductance in a network ($G_{hk}$) and the equation
| $ R_{h2} = \displaystyle\frac{1}{ G_{h2} }$ |
leads to the parallel total hydraulic conductance ($G_{pt}$) can be calculated with:
| $ G_{pt} =\displaystyle\sum_k G_{hk} $ |
ID:(15948, 0)
Darcy's law and hydraulic resistance (1)
Equation
Darcy rewrites the Hagen Poiseuille equation so that the pressure difference ($\Delta p$) is equal to the hydraulic resistance ($R_h$) times the volume flow ($J_V$):
 $ \Delta p = R_{h1} J_{V1} $ |
 $ \Delta p = R_h J_V $ |
The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:
| $ J_V = G_h \Delta p $ |
Furthermore, using the relationship for the hydraulic resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
results in:
| $ \Delta p = R_h J_V $ |
ID:(3179, 1)
Darcy's law and hydraulic resistance (2)
Equation
Darcy rewrites the Hagen Poiseuille equation so that the pressure difference ($\Delta p$) is equal to the hydraulic resistance ($R_h$) times the volume flow ($J_V$):
| $ \Delta p = R_{h2} J_{V2} $ |
| $ \Delta p = R_h J_V $ |
The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:
| $ J_V = G_h \Delta p $ |
Furthermore, using the relationship for the hydraulic resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
results in:
| $ \Delta p = R_h J_V $ |
ID:(3179, 2)
Darcy's law and hydraulic resistance (3)
Equation
Darcy rewrites the Hagen Poiseuille equation so that the pressure difference ($\Delta p$) is equal to the hydraulic resistance ($R_h$) times the volume flow ($J_V$):
| $ \Delta p = R_{h3} J_{V3} $ |
| $ \Delta p = R_h J_V $ |
The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:
| $ J_V = G_h \Delta p $ |
Furthermore, using the relationship for the hydraulic resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
results in:
| $ \Delta p = R_h J_V $ |
ID:(3179, 3)
Darcy's law and hydraulic resistance (4)
Equation
Darcy rewrites the Hagen Poiseuille equation so that the pressure difference ($\Delta p$) is equal to the hydraulic resistance ($R_h$) times the volume flow ($J_V$):
| $ \Delta p = R_{pt} J_{Vt} $ |
| $ \Delta p = R_h J_V $ |
The volume flow ($J_V$) can be calculated from the hydraulic conductance ($G_h$) and the pressure difference ($\Delta p$) using the following equation:
| $ J_V = G_h \Delta p $ |
Furthermore, using the relationship for the hydraulic resistance ($R_h$):
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
results in:
| $ \Delta p = R_h J_V $ |
ID:(3179, 4)
Darcy's law and hydraulic conductance (1)
Equation
With the introduction of the hydraulic conductance ($G_h$), we can rewrite the Hagen-Poiseuille equation with the pressure difference ($\Delta p$) and the volume flow ($J_V$) using the following equation:
| $ J_{V1} = G_{h1} \Delta p $ |
| $ J_V = G_h \Delta p $ |
If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
to arrive at:
| $ J_V = G_h \Delta p $ |
ID:(14471, 1)
Darcy's law and hydraulic conductance (2)
Equation
With the introduction of the hydraulic conductance ($G_h$), we can rewrite the Hagen-Poiseuille equation with the pressure difference ($\Delta p$) and the volume flow ($J_V$) using the following equation:
| $ J_{V2} = G_{h2} \Delta p $ |
| $ J_V = G_h \Delta p $ |
If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
to arrive at:
| $ J_V = G_h \Delta p $ |
ID:(14471, 2)
Darcy's law and hydraulic conductance (3)
Equation
With the introduction of the hydraulic conductance ($G_h$), we can rewrite the Hagen-Poiseuille equation with the pressure difference ($\Delta p$) and the volume flow ($J_V$) using the following equation:
| $ J_{V3} = G_{h3} \Delta p $ |
| $ J_V = G_h \Delta p $ |
If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
to arrive at:
| $ J_V = G_h \Delta p $ |
ID:(14471, 3)
Darcy's law and hydraulic conductance (4)
Equation
With the introduction of the hydraulic conductance ($G_h$), we can rewrite the Hagen-Poiseuille equation with the pressure difference ($\Delta p$) and the volume flow ($J_V$) using the following equation:
| $ J_{Vt} = G_{pt} \Delta p $ |
| $ J_V = G_h \Delta p $ |
If we examine the Hagen-Poiseuille law, which allows us to calculate the volume flow ($J_V$) from the tube radius ($R$), the viscosity ($\eta$), the tube length ($\Delta L$), and the pressure difference ($\Delta p$):
| $ J_V =-\displaystyle\frac{ \pi R ^4}{8 \eta }\displaystyle\frac{ \Delta p }{ \Delta L }$ |
we can introduce the hydraulic conductance ($G_h$), defined in terms of the tube length ($\Delta L$), the tube radius ($R$), and the viscosity ($\eta$), as follows:
| $ G_h =\displaystyle\frac{ \pi R ^4}{8 \eta | \Delta L | }$ |
to arrive at:
| $ J_V = G_h \Delta p $ |
ID:(14471, 4)
Hydraulic conductance (1)
Equation
In the context of electrical resistance, there exists its inverse, known as electrical conductance. Similarly, what would be the hydraulic conductance ($G_h$) can be defined in terms of the hydraulic resistance ($R_h$) through the expression:
| $ R_{h1} = \displaystyle\frac{1}{ G_{h1} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 1)
Hydraulic conductance (2)
Equation
In the context of electrical resistance, there exists its inverse, known as electrical conductance. Similarly, what would be the hydraulic conductance ($G_h$) can be defined in terms of the hydraulic resistance ($R_h$) through the expression:
| $ R_{h2} = \displaystyle\frac{1}{ G_{h2} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 2)
Hydraulic conductance (3)
Equation
In the context of electrical resistance, there exists its inverse, known as electrical conductance. Similarly, what would be the hydraulic conductance ($G_h$) can be defined in terms of the hydraulic resistance ($R_h$) through the expression:
| $ R_{h3} = \displaystyle\frac{1}{ G_{h3} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 3)
Hydraulic conductance (4)
Equation
In the context of electrical resistance, there exists its inverse, known as electrical conductance. Similarly, what would be the hydraulic conductance ($G_h$) can be defined in terms of the hydraulic resistance ($R_h$) through the expression:
| $ R_{pt} = \displaystyle\frac{1}{ G_{pt} }$ |
| $ R_h = \displaystyle\frac{1}{ G_h }$ |
ID:(15092, 4)
Hydraulic conductance in parallel (3)
Equation
The parallel connection of the hydraulic conductance 1 ($G_{h1}$), the hydraulic conductance 2 ($G_{h2}$), and the hydraulic conductance 3 ($G_{h3}$) results in an equivalent combination of the parallel total hydraulic conductance ($G_{pt}$):
| $ G_{pt} = G_{h1} + G_{h2} + G_{h3} $ |
ID:(3857, 0)
Total flow (3)
Equation
The flujo de Volumen Total ($J_{Vt}$) represents the total sum of the individual contributions from the volume flow 1 ($J_{V1}$), the volume flow 2 ($J_{V2}$), and the volume flow 3 ($J_{V3}$), from the elements connected in parallel:
| $ J_{Vt} = J_{V1} + J_{V2} + J_{V3} $ |
ID:(12801, 0)
Sum of resistors in parallel (3)
Equation
The parallel combination of the hydraulic Resistance 1 ($R_{h1}$), the hydraulic Resistance 2 ($R_{h2}$), and the hydraulic Resistance 3 ($R_{h3}$) results in a total equivalent of the total hydraulic resistance in series ($R_{st}$):
| $\displaystyle\frac{1}{ R_{pt} }=\displaystyle\frac{1}{ R_{h1} }+\displaystyle\frac{1}{ R_{h2} }+\displaystyle\frac{1}{ R_{h3} }$ |
ID:(3859, 0)