Conductores y Aislantes
Storyboard 
En el caso de los aislantes las cargas no se desplazan lo que lleva a que el material no puede ser polarizado. En los conductores las cargas se desplazan polarizándose modificando el campo. Las capacitancias por lo general tienen materiales dieléctricos entre las placas que son capaces de polarizarse aumentando la capacitancia.
ID:(1572, 0)
Polarización de un cuerpo, conductor en campo eléctrico
Definición 
Si colocamos un cuerpo conductor dentro de un campo eléctrico en primera instancia las lineas de campo lo atraviesan sin sufrir alteración:

ID:(11618, 0)
Polarización de un cuerpo, polarización del conductor
Imagen 
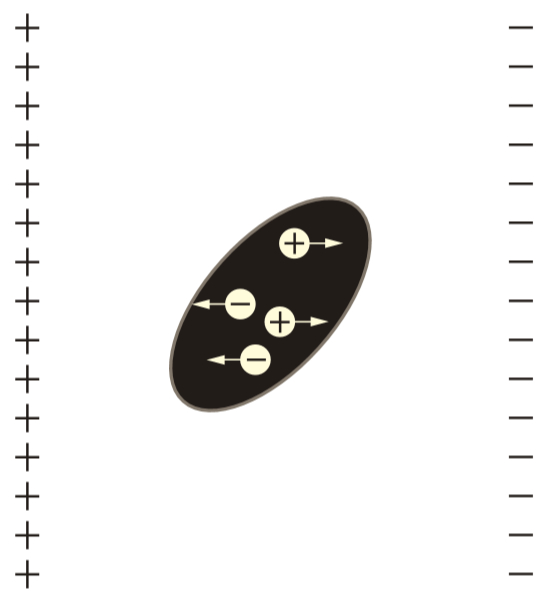
Como las cargas en el conductor son libres de desplazarse, comienzan a migrar en la dirección del campo:
• las negativas se dirigen en dirección del origen de las lineas de campo (cargas positivas)
• las positivas se dirigen en dirección del destino de las líneas de campo (cargas negativas)
de esta forma el conductor termina polarizado:
ID:(11619, 0)
Polarización de un cuerpo, modificación del campo eléctrico
Nota 
Con el cuerpo polarizado el campo se modifica interrumpiendo se las lineas de campo originales 'se cortan' y
• aquellas que proceden del origen (cargas positivas) y son próximas al conductor terminan en las cargas negativas de este
• aquellas que se dirigían al destino (cargas negativas) y son próximas al conductor nacen ahora de las cargas positivas de este

ID:(11620, 0)
Conductores y Aislantes
Descripción 
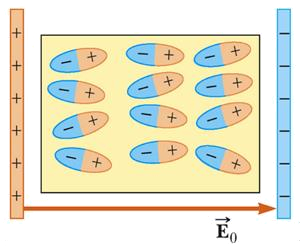
En el caso de los aislantes las cargas no se desplazan lo que lleva a que el material no puede ser polarizado. En los conductores las cargas se desplazan polarizándose modificando el campo. Las capacitancias por lo general tienen materiales dieléctricos entre las placas que son capaces de polarizarse aumentando la capacitancia.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Si colocamos un cuerpo conductor dentro de un campo el ctrico en primera instancia las lineas de campo lo atraviesan sin sufrir alteraci n:

(ID 11618)
Como las cargas en el conductor son libres de desplazarse, comienzan a migrar en la direcci n del campo:
• las negativas se dirigen en direcci n del origen de las lineas de campo (cargas positivas)
• las positivas se dirigen en direcci n del destino de las l neas de campo (cargas negativas)
de esta forma el conductor termina polarizado:

(ID 11619)
Con el cuerpo polarizado el campo se modifica interrumpiendo se las lineas de campo originales 'se cortan' y
• aquellas que proceden del origen (cargas positivas) y son pr ximas al conductor terminan en las cargas negativas de este
• aquellas que se dirig an al destino (cargas negativas) y son pr ximas al conductor nacen ahora de las cargas positivas de este

(ID 11620)
(ID 1699)
Si se define una superficie que pasa entre las placas y rodea la carga
$E_dS=\displaystyle\frac{Q}{\epsilon\epsilon_0}$
con
Como por otro lado el campo es igual a la diferencia de potencial
$\Delta\varphi = \displaystyle\frac{\sigma}{\epsilon\epsilon_0}d=E_dd=\displaystyle\frac{Q}{\epsilon\epsilon_0}\displaystyle\frac{d}{S}$
se obtiene con la definici n
$\Delta\varphi=\displaystyle\frac{Q}{C}$
que la capacidad de dos placas se puede calcular con
| $ C = \epsilon_0 \epsilon \displaystyle\frac{ S }{ d }$ |
(ID 3865)
ID:(1572, 0)
