Résistance
Storyboard 
Le flux autour d'une aile entraîne la formation de tourbillons qui, en fonction de la forme et de l'angle de l'aile par rapport à l'écoulement, peut générer des tourbillons dans une section de celle-ci. Si l'on considère des éléments de volume autour de l'aile et que l'on suppose que la conservation de l'énergie peut être localement appliquée, différentes vitesses entraîneront différentes pressions (loi de Bernoulli) sur la surface.
La somme de toutes les pressions sur la surface dans la direction du vol, à la fois devant l'aile (force vers l'arrière) et derrière l'aile (force vers l'avant), conduit à une force totale que l'on appelle traînée. Pour propulser un corps (avion/oiseau), il est nécessaire que la poussée surmonte cette force de traînée.
ID:(464, 0)
Résistance
Storyboard 
Le flux autour d'une aile entraîne la formation de tourbillons qui, en fonction de la forme et de l'angle de l'aile par rapport à l'écoulement, peut générer des tourbillons dans une section de celle-ci. Si l'on considère des éléments de volume autour de l'aile et que l'on suppose que la conservation de l'énergie peut être localement appliquée, différentes vitesses entraîneront différentes pressions (loi de Bernoulli) sur la surface. La somme de toutes les pressions sur la surface dans la direction du vol, à la fois devant l'aile (force vers l'arrière) et derrière l'aile (force vers l'avant), conduit à une force totale que l'on appelle traînée. Pour propulser un corps (avion/oiseau), il est nécessaire que la poussée surmonte cette force de traînée.
Variables
Calculs
Calculs
Équations
A force de levage ($F_L$), en compagnie de a envergure des ailes ($L$), a densité ($\rho$), le facteur de vitesse maximale de l'aile ($c_t$), le facteur de vitesse en bas d'aile ($c_b$), a longueur de l'aile supérieure ($l_t$), a longueur de l'aile inférieure ($l_b$) et a vitesse par rapport au milieu ($v$), se trouve dans
Si nous consid rons a surface génératrice de portance ($S_w$), d fini par a envergure des ailes ($L$), a longueur de l'aile supérieure ($l_t$) et a longueur de l'aile inférieure ($l_b$),
et pour le coefficient de portance ($C_L$), d fini comme
nous obtenons
De mani re similaire la fa on dont l' quation pour a force de levage ($F_L$) a t d riv e en utilisant a densité ($\rho$), le coefficient de portance ($C_L$), a surface génératrice de portance ($S_w$) et a vitesse par rapport au milieu ($v$)
dans cette analogie, ce qui correspond a surface génératrice de portance ($S_w$) sera quivalent le profil total de l'objet ($S_p$) et le coefficient de portance ($C_L$) Le coefficient de résistance ($C_W$), ce qui permet de calculer a force de résistance ($F_W$) :
Le coefficient de tra n e est mesur et, dans les coulements turbulents sur les corps a rodynamiques, les valeurs sont g n ralement autour de 0.4.
En utilisant les relations de a force de résistance totale ($F_R$) avec a force de levage ($F_L$), a force de résistance ($F_W$), et le accélération maximale ($\alpha$) :
nous pouvons calculer en utilisant la force de r sistance avec a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$), et a vitesse par rapport au milieu ($v$) :
et la force de portance avec a surface génératrice de portance ($S_w$) et le coefficient de portance ($C_L$) :
en utilisant la relation pour le coefficient de portance ($C_L$) avec a constante de proportionnalité du coefficient de portance ($c$) :
en utilisant la relation pour le sinus du petit angle d'attaque $\alpha$ :
et le cosinus :
avec la condition d' quilibrer le poids de l'oiseau ou de l'a ronef pour a masse corporelle ($m$) et a accélération gravitationnelle ($g$) :
nous obtenons :
La composante horizontale de la force de sustentation correspond la force $F_L$ multipli e par le sinus de l'angle d'attaque $\alpha$:
$F_L \sin\alpha $
et la composante horizontale de la force de r sistance correspond la force $F_W$ multipli e par le cosinus de l\'angle d\'attaque $\alpha$:
$F_W \cos\alpha $
Par cons quent, la force totale de r sistance se calcule de la mani re suivante :
Le sinus peut tre calcul en utilisant un polyn me de la forme :
$\sin \alpha = \alpha - \displaystyle\frac{1}{3!}\alpha^3 + \displaystyle\frac{1}{5!}\alpha^5 \ldos$
Pour de petites valeurs de le accélération maximale ($\alpha$) ($\alpha \ll 1$), les termes avec des puissances sup rieures sont n gligeables, et nous obtenons :
Le cosinus peut tre calcul l'aide d'un polyn me de la forme :
$\cos \alpha = 1 - \displaystyle\frac{1}{2!}\alpha^2 + \displaystyle\frac{1}{4!}\alpha^4 \ldots$
Pour de petites valeurs de le accélération maximale ($\alpha$) ($\alpha \ll 1$), les termes avec des puissances sup rieures sont n gligeables, et nous obtenons :
Exemples
En observant l' coulement moyen autour d'une aile, on peut remarquer que les lignes au-dessus de l'aile sont plus longues que celles en dessous. En termes simplifi s, on argumente qu'en raison de ce trajet plus long, on s'attend ce que a vitesse au sommet ($v_t$) soit sup rieur a vitesse en bas ($v_b$), bien que les deux soient sup rieurs a vitesse par rapport au milieu ($v$).
Si la loi de Bernoulli est applicable, la diff rence de vitesses entra nerait une diff rence de pressions agissant sur l'aile. En particulier, si a vitesse au sommet ($v_t$) est sup rieur, son correspondant a pression sur le dessus de l'aile ($p_t$) serait inf rieur celui avec a vitesse en bas ($v_b$) et son correspondant a pression sur le bas de l'aile ($p_b$). Cela impliquerait l'existence d'un a force de levage ($F_L$) en raison de l'effet de cette diff rence de pression.
Cependant, comme on le voit vers la fin du profil de l'aile (c t droit), des turbulences se forment, limitant l'applicabilit du principe de Bernoulli. En particulier, il convient de consid rer qu'en certaines parties de la circonf rence de l'aile, son application peut tre limit e et ne contribuera pas la portance.
L'objet ne g n re pas seulement de la portance, mais cr e galement une r sistance au flux d'air autour de lui. Bien que l'application directe du principe de Bernoulli puisse ne pas tre faisable, nous pouvons toujours comprendre le type d'effet attendre, m me s'il doit tre mod lis diff remment. Dans ce contexte, l'extr mit de l'aile, la vitesse est nulle, ce qui entra ne une pression maximale. De m me, l'extr mit arri re de l'objet, la vitesse est maximale, ce qui entra ne une pression minimale. Cela g n re une pression qui s'oppose au mouvement vers l'avant de l'objet, correspondant la r sistance.
Cependant, il est important de noter que cet argument n'est que partiellement correct. En particulier, des turbulences sont g n r es l'extr mit arri re de l'aile, ce qui complique l'argument de haute vitesse et remet en question l'application du principe de Bernoulli.
En suivant l'approche de mod lisation utilis e pour la portance, nous pouvons supposer que le th or me de Kutta-Joukowski, dans lequel a force de levage ($F_L$) avec a densité ($\rho$), a vitesse par rapport au milieu ($v$) et a circulation aérodynamique ($\Gamma$), est le suivant :
Nous pouvons supposer qu'il est vectoriel, ce qui signifie qu'il a une composante verticale expliquant la portance et une composante horizontale mod lisant la r sistance.
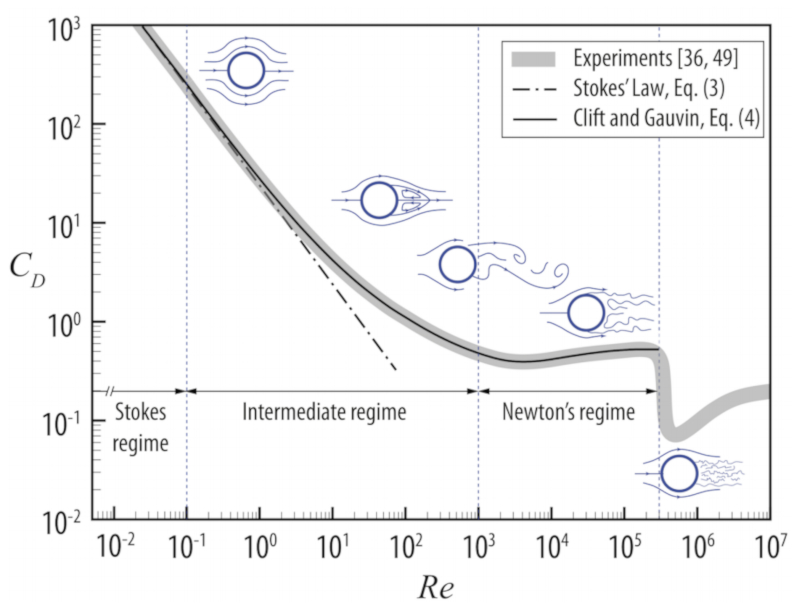
Le coefficient de r sistance $C_d$ est souvent une fonction du nombre de Reynolds $Re$. Dans le cas d'une sph re, le coefficient de r sistance prend la forme suivante :
Dans la plage de faibles nombres de Reynolds, le coefficient de r sistance est inversement proportionnel la vitesse $1/v$, ce qui signifie que dans cette plage, la force de tra n e est proportionnelle la vitesse (loi de Stokes).
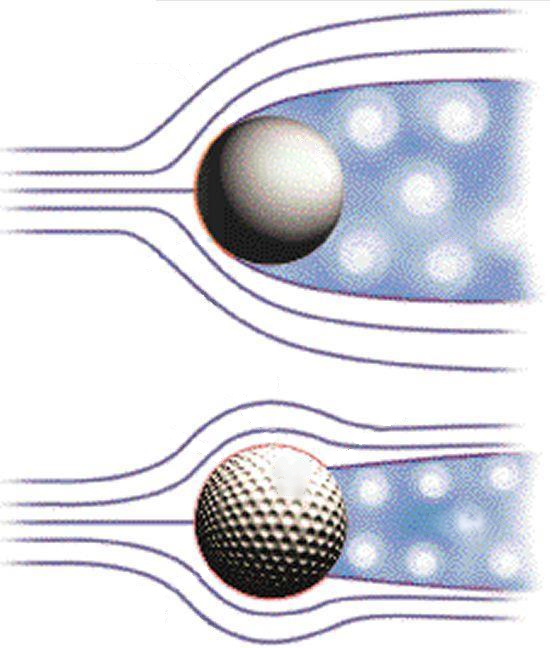
Dans la plage de grands nombres de Reynolds, le coefficient de r sistance devient constant, ce qui implique que la force de tra n e est proportionnelle au carr de la vitesse. Cependant, il est important de noter qu\'il y a une discontinuit o le coefficient diminue brusquement. Cette diminution correspond une situation o la zone de turbulence se r duit.
Si l\'objectif est de r duire la r sistance d\'une balle, il est n cessaire d\'augmenter le nombre de Reynolds pour profiter de la diminution du coefficient de r sistance. Cela peut tre r alis en introduisant des rainures, telles que celles pr sentes sur une balle de golf. Ces rainures agissent comme de petits s parateurs qui maintiennent la couche d\'air coll e la balle, permettant au flux de rester plus lin aire pendant une plus longue p riode de temps et r duisant ainsi la surface qui g n re la r sistance.
Lorsque l'aile est inclin e, elle g n re non seulement de la portance mais aussi une composante de tra n e, car la direction de la portance est orthogonale la surface de l'aile. Si nous repr sentons graphiquement a force de levage ($F_L$), a force de résistance ($F_W$) et le accélération maximale ($\alpha$), nous obtenons :
D'apr s les travaux de Kutta [1] et Joukowski [2], un th or me a t d velopp montrant l'association entre a circulation aérodynamique ($\Gamma$) et a force de levage ($F_L$) travers a envergure des ailes ($L$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$) comme suit :
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sur la t che de la th orie des ailes et une nouvelle m thode pour sa d rivation), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sur la conservation du cercle d'air autour d'un profil), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
Pour g n rer une pression plus lev e en dessous qu'au-dessus de l'aile et produire de la portance, le principe de Bernoulli est utilis pour corriger le manque de conservation de la densit d' nergie avec un coefficient de portance ($C_L$). La pression sur l'aile, a force de levage ($F_L$), peut tre estim e en utilisant a densité ($\rho$), a surface génératrice de portance ($S_w$), le coefficient de portance ($C_L$), et a vitesse par rapport au milieu ($v$) gr ce la formule suivante :
A force de résistance ($F_W$) peut tre calcul en utilisant a densité ($\rho$), le coefficient de résistance ($C_W$), le profil total de l'objet ($S_p$) et a vitesse par rapport au milieu ($v$) selon le formule suivante :
La force totale de r sistance est compos e des composantes horizontales de la force de r sistance du profil de l'aile $F_W$ et de la force de portance $F_L$, qui peuvent tre calcul es partir de l'angle d\'attaque $\alpha$:
partir de mesures, il est conclu que le coefficient de portance $C_L$ est proportionnel l'angle d\'attaque $\alpha$:
Apr s un certain angle, la courbe diminue jusqu\' atteindre z ro. Cela est d au fait que au-del de cet angle critique, les tourbillons recouvrent enti rement la surface sup rieure de l\'aile, ce qui entra ne une perte de portance. Ce ph nom ne est appel \"d crochage\" ou \"d crochage a rodynamique\".
Pour de petits angles, la fonction sinus peut tre approxim e par une droite qui passe par l'origine. Si le accélération maximale ($\alpha$) est exprim en radians, la pente de cette droite est gale un, et nous obtenons :
Pour de petites valeurs de le accélération maximale ($\alpha$), la fonction cosinus peut tre approxim e par une parabole invers e qui passe par l'origine. Si l'angle est exprim en radians et est approximativement nul, nous obtenons :
Pour calculer a force de résistance totale ($F_R$), nous supposons de petits angles et consid rons une situation o l'angle est tel qu'il maintient a masse corporelle ($m$). En utilisant cette approximation et les variables le coefficient de portance ($C_L$), le coefficient de résistance ($C_W$), a surface génératrice de portance ($S_w$), le profil total de l'objet ($S_p$), a accélération gravitationnelle ($g$), a constante de proportionnalité du coefficient de portance ($c$), a densité ($\rho$) et a vitesse par rapport au milieu ($v$), nous obtenons l'expression suivante :
ID:(464, 0)