Resistencia
Storyboard 
El flujo en torno a un ala lleva la formación de torbellinos que según la forma y angulo del ala con respecto del flujo puede originar torbellinos en una sección de estos. Si se consideran elementos de volumen en torno del ala y se asume que se puede locamente asumir conservación de energía se tiene que las distintas velocidades llevaran a distintas presiones (Bernoulli) sobre la superficie.
La suma de todas las presiones sobre la superficie en la dirección de vuelo, tanto por delante del ala (fuerza hacia atrás) como detrás del ala (fuerza hacia adelante) llevan a una fuerza total que denominamos resistencia. Para poder impulsar un cuerpo (avión/ave) es necesario que la propulsión supere esta fuerza de resistencia.
ID:(464, 0)
Resistencia
Storyboard 
El flujo en torno a un ala lleva la formación de torbellinos que según la forma y angulo del ala con respecto del flujo puede originar torbellinos en una sección de estos. Si se consideran elementos de volumen en torno del ala y se asume que se puede locamente asumir conservación de energía se tiene que las distintas velocidades llevaran a distintas presiones (Bernoulli) sobre la superficie. La suma de todas las presiones sobre la superficie en la dirección de vuelo, tanto por delante del ala (fuerza hacia atrás) como detrás del ala (fuerza hacia adelante) llevan a una fuerza total que denominamos resistencia. Para poder impulsar un cuerpo (avión/ave) es necesario que la propulsión supere esta fuerza de resistencia.
Variables
Cálculos
Cálculos
Ecuaciones
La fuerza de sustentación ($F_L$), junto con la envergadura de las alas ($L$), la densidad ($\rho$), el factor de velocidad superior del ala ($c_t$), el factor de velocidad inferior del ala ($c_b$), la largo superior del ala ($l_t$), la largo inferior del ala ($l_b$) y la velocidad respecto del medio ($v$), se encuentra en
Si consideramos la superficie que genera sustentación ($S_w$), definido por la envergadura de las alas ($L$), la largo superior del ala ($l_t$) y la largo inferior del ala ($l_b$),
y para el coeficiente de sustentación ($C_L$), definido como
obtenemos
De forma similar a c mo se deriv la ecuaci n para la fuerza de sustentación ($F_L$) utilizando la densidad ($\rho$), el coeficiente de sustentación ($C_L$), la superficie que genera sustentación ($S_w$) y la velocidad respecto del medio ($v$)
en esta analog a, lo que corresponde a la superficie que genera sustentación ($S_w$) ser equivalente a el perfil total del objeto ($S_p$) y el coeficiente de sustentación ($C_L$) a el coeficiente de resistencia ($C_W$), con lo que se calcula la fuerza de resistencia ($F_W$):
El coeficiente de resistencia se mide y, en flujos turbulentos sobre cuerpos aerodin micos, generalmente se registran valores alrededor de 0.4.
Utilizando las relaciones de la fuerza total de resistencia ($F_R$) con la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$) y el angulo de ataque del ala ($\alpha$):
podemos calcular la fuerza de resistencia utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$):
y la fuerza de sustentaci n con la superficie que genera sustentación ($S_w$) y el coeficiente de sustentación ($C_L$):
utilizando la relaci n para el coeficiente de sustentación ($C_L$) con la constante de proporcionalidad del coeficiente de sustentación ($c$):
usando la relaci n para el seno del ngulo de ataque $\alpha$ peque o:
y el coseno:
con la condici n de equilibrar el peso del ave o avi n para la masa del cuerpo ($m$) y la aceleración gravitacional ($g$):
obtenemos:
La componente horizontal de la fuerza de sustentación ($F_L$) corresponde a la fuerza de sustentación ($F_L$) multiplicada por el seno del ERROR:6121,0:
$F_L \sin\alpha $
y la componente horizontal de la fuerza de resistencia ($F_W$) corresponde a la fuerza de resistencia ($F_W$) multiplicada por el coseno del ngulo de ERROR:6121,0:
$F_W \cos\alpha $
Por lo tanto, la fuerza total de resistencia ($F_R$) se calcula como:
El seno se puede calcular utilizando un polinomio de la forma:
$\sin \alpha = \alpha - \displaystyle\frac{1}{3!}\alpha^3 + \displaystyle\frac{1}{5!}\alpha^5 \ldos$
Para valores peque os de el angulo de ataque del ala ($\alpha$) ($\alpha \ll 1$), los t rminos con potencias superiores son despreciables, y obtenemos:
El coseno se puede calcular utilizando un polinomio de la forma:
$\cos \alpha = 1 - \displaystyle\frac{1}{2!}\alpha^2 + \displaystyle\frac{1}{4!}\alpha^4 \ldots$
Para valores peque os de el angulo de ataque del ala ($\alpha$) ($\alpha \ll 1$), los t rminos con potencias superiores son despreciables, y obtenemos:
Ejemplos
Al observar el flujo promedio alrededor de un ala, se puede notar que las l neas sobre el ala son m s largas que las del lado inferior. En t rminos simplificados, se argumenta que debido a esta trayectoria m s larga, se espera que la velocidad en la parte superior ($v_t$) sea mayor que la velocidad en la parte inferior ($v_b$), aunque ambos sean superiores a la velocidad respecto del medio ($v$).
Si la ley de Bernoulli es aplicable, la diferencia de velocidades resultar a en una diferencia de presiones que act an sobre el ala. En particular, si la velocidad en la parte superior ($v_t$) es mayor, su correspondiente la presión en la parte superior del ala ($p_t$) ser a menor que con la velocidad en la parte inferior ($v_b$) y su correspondiente la presión en la parte Inferior del ala ($p_b$). Esto implicar a la existencia de una la fuerza de sustentación ($F_L$) debido al efecto de esta diferencia de presi n.
Sin embargo, como se ve hacia el final del perfil del ala (lado derecho), se forman turbulencias, lo que limita la aplicabilidad del principio de Bernoulli. Espec ficamente, se debe considerar que en una cierta parte del per metro del ala, puede que no sea aplicable y no contribuir a la sustentaci n.
El objeto no solo genera sustentaci n, sino que tambi n genera resistencia al flujo de aire en su entorno. Aunque la ley de Bernoulli no se pueda aplicar directamente, podemos entender el tipo de efecto que podr a esperarse, incluso si es necesario modelarlo de otra manera. En este sentido, en el flujo en la punta del ala, la velocidad es nula y, por lo tanto, la presi n es m xima. De manera an loga, en la parte posterior del objeto, la velocidad ser a m xima y, por lo tanto, la presi n ser a m nima. Esto genera una presi n que se opone al avance del objeto y, por lo tanto, corresponde a una resistencia.
Sin embargo, es importante tener en cuenta que este argumento es solo parcialmente correcto. En particular, se generan turbulencias en la parte posterior del ala, lo que complica el argumento de alta velocidad y tambi n cuestiona el uso de la ley de Bernoulli.
Siguiendo la forma en que se model el proceso para el caso de la sustentaci n, podemos asumir que el teorema Kutta-Joukowski, en el que la fuerza de sustentación ($F_L$) con la densidad ($\rho$), la velocidad respecto del medio ($v$) y la circulación aerodinamica ($\Gamma$) es:
Podemos asumir que es vectorial, lo que significa que tiene una componente vertical que explica la sustentaci n y una componente horizontal que modela la resistencia.
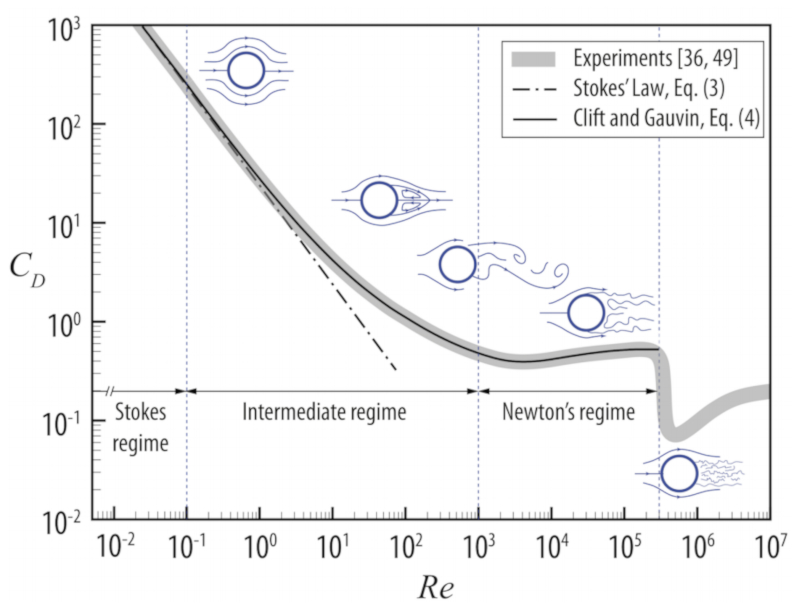
El coeficiente de resistencia ($C_W$) a menudo es una funci n del la número de Reynolds ($Re$). En el caso de una esfera, el coeficiente de resistencia tiene la forma:
En el rango de bajos n meros de Reynolds, el coeficiente de resistencia es proporcionalmente inverso a la velocidad $1/v$:
$C_W =\displaystyle\frac{24}{Re}$
lo que significa que en este rango, la fuerza de resistencia es proporcional a la velocidad (ley de Stokes).
En el rango de altos n meros de Reynolds, el coeficiente de resistencia crece muy lentamente como
$C_W=\displaystyle\frac{0.44}{Re^{0.2}}$
lo que implica que la fuerza de resistencia es proporcional a la velocidad al cuadrado. Sin embargo, es importante destacar que hay una discontinuidad en la cual el coeficiente se reduce bruscamente. Esta reducci n corresponde a una situaci n en la que la zona de turbulencia disminuye.
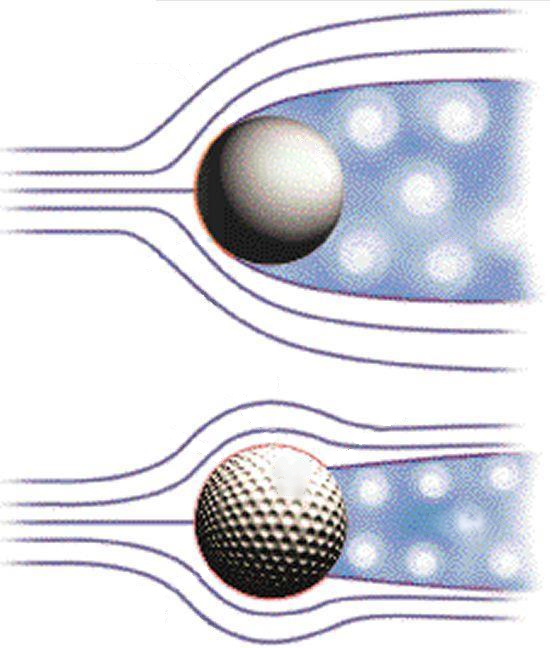
Si se desea reducir la resistencia de una pelota, es necesario aumentar el n mero de Reynolds para aprovechar la disminuci n del coeficiente de resistencia. Esto se logra introduciendo ranuras, como las que tiene una pelota de golf. Estas ranuras act an como peque os separadores que mantienen la capa de aire adherida a la pelota, lo que hace que el flujo permanezca m s lineal durante m s tiempo, reduciendo as la secci n que genera resistencia.
Al inclinar el ala, no solo se genera sustentaci n; una parte de esta tambi n genera resistencia, ya que la direcci n de la sustentaci n es ortogonal a la superficie del ala. Si representamos gr ficamente la fuerza de sustentación ($F_L$), la fuerza de resistencia ($F_W$) y el angulo de ataque del ala ($\alpha$), obtenemos:
De los trabajos de Kutta [1] y Joukowski [2] se deriv un teorema que establece una relaci n entre la circulación aerodinamica ($\Gamma$) y la fuerza de sustentación ($F_L$) a trav s de la envergadura de las alas ($L$), la densidad ($\rho$) y la velocidad respecto del medio ($v$) mediante la siguiente f rmula:
[1] " ber die Aufgabe der Fl geltheorie und ein neues Verfahren zur Herleitung derselben." (Sobre la tarea de la teor a de alas y un nuevo m todo para su derivaci n.), Martin Wilhelm Kutta, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1902)
[2] " ber die Erhaltung des Luftkreises um ein Profil." (Sobre la conservaci n del c rculo de aire alrededor de un perfil.), Nikolai Zhukovsky, Nachrichten von der Gesellschaft der Wissenschaften zu G ttingen, Mathematisch-Physikalische Klasse (1904)
Para crear una presi n mayor debajo que encima del ala y generar sustentaci n, se emplea la Ley de Bernoulli, corrigiendo la falta de conservaci n de la densidad de energ a mediante un coeficiente de sustentación ($C_L$). La presi n sobre el ala, la fuerza de sustentación ($F_L$), se puede estimar utilizando la densidad ($\rho$), la superficie que genera sustentación ($S_w$), el coeficiente de sustentación ($C_L$) y la velocidad respecto del medio ($v$) mediante la siguiente f rmula:
La fuerza de resistencia ($F_W$) se puede calcular utilizando la densidad ($\rho$), el coeficiente de resistencia ($C_W$), el perfil total del objeto ($S_p$) y la velocidad respecto del medio ($v$) de acuerdo con la siguiente f rmula:
La fuerza total de resistencia ($F_R$) se compone de las componentes horizontales de la fuerza de resistencia ($F_W$) y de la fuerza de sustentación ($F_L$), que se puede calcular a partir del ERROR:6121,0:
A partir de mediciones, se concluye que el coeficiente de sustentación ($C_L$) es proporcional al ERROR:6121,0 siendo la constante de proporcionalidad del coeficiente de sustentación ($c$):
Despu s de cierto ngulo, la curva disminuye hasta llegar a cero. Esto se debe a que sobre dicho ngulo cr tico, los v rtices cubren completamente la superficie superior del ala, lo que resulta en la p rdida de sustentaci n. Este fen meno se conoce como "stall" (entrada en p rdida).
Para ngulos peque os, la funci n seno se puede aproximar por una recta que pasa por el origen. Si expresamos el angulo de ataque del ala ($\alpha$) en radianes, la pendiente de esta recta es igual a la unidad y obtenemos:
Para valores peque os de el angulo de ataque del ala ($\alpha$), la funci n coseno se puede aproximar por una par bola invertida que pasa por el origen. Si el ngulo se expresa en radianes y es aproximadamente cero, obtenemos:
Para calcular la fuerza total de resistencia ($F_R$), suponemos ngulos peque os y consideramos una situaci n en la que el ngulo permite mantener la masa del cuerpo ($m$). Utilizando esta aproximaci n y las variables el coeficiente de sustentación ($C_L$), el coeficiente de resistencia ($C_W$), la superficie que genera sustentación ($S_w$), el perfil total del objeto ($S_p$), la aceleración gravitacional ($g$), la constante de proporcionalidad del coeficiente de sustentación ($c$), la densidad ($\rho$) y la velocidad respecto del medio ($v$), obtenemos la siguiente expresi n:
ID:(464, 0)