Aceleración instantánea
Storyboard 
Para describir como evoluciona la velocidad en el tiempo se debe estudiar la variación de esta en el tiempo.
La relación de la variación de la velocidad equivale a la variación de la velocidad en el tiempo transcurrido que, dividido por este se, corresponde a la aceleración.
Para un tiempo transcurrido infinitesimal la aceleración corresponde a la aceleración instantánea.
ID:(1433, 0)
Aceleración instantánea
Storyboard 
Para describir como evoluciona la velocidad en el tiempo se debe estudiar la variación de esta en el tiempo. La relación de la variación de la velocidad equivale a la variación de la velocidad en el tiempo transcurrido que, dividido por este se, corresponde a la aceleración. Para un tiempo transcurrido infinitesimal la aceleración corresponde a la aceleración instantánea.
Variables
Cálculos
Cálculos
Ecuaciones
Como un vector se puede expresar como un arreglo de sus diferentes componentes
$\vec{v}=(v_x,v_y,v_z)$
su derivada se puede expresar como la derivada de cada una de sus componentes
$\displaystyle\frac{d}{dt}\vec{v}=\displaystyle\frac{d}{dt}(v_x,v_y,v_z)=\left(\displaystyle\frac{dv_x}{dt},\displaystyle\frac{dv_y}{dt},\displaystyle\frac{dv_z}{dt}\right)=\displaystyle\frac{d\vec{v}}{dt}=\vec{a}$
se tiene que en general la velocidad instantanea en mas de una dimensi n es
Si consideramos la diferencia de la velocidad ($v$) en los tiempos $t+\Delta t$ y $t$:
$\Delta v = v(t+\Delta t)-v(t)$
y tomamos $\Delta t$ como el tiempo transcurrido ($\Delta t$), entonces en el l mite de tiempos infinitesimalmente cortos:
$a=\displaystyle\frac{\Delta v}{\Delta t}=\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t} \rightarrow \lim_{\Delta t\rightarrow 0}\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}=\displaystyle\frac{dv}{dt}$
Esta ltima expresi n corresponde a la derivada de la funci n la velocidad ($v$):
la cual, a su vez, es la pendiente de la representaci n gr fica de dicha funci n en el tiempo ($t$).
Si integramos en el tiempo ($t$) la definici n de la aceleración instantanea ($a$),
esto significa que para un intervalo de tiempo $dt$, la distancia recorrida es
$dv = a dt$
Si consideramos $N$ intervalos $dt_i$ con aceleraciones $a_i$, la variaci n total en la velocidad ser
$v - v_0 = \displaystyle\sum_i a_i dt_i$
Si consideramos la curva de aceleraci n-tiempo, los elementos $a_i dt_i$ corresponden a rect ngulos con altura $a_i$ y ancho $dt_i$. La suma, por lo tanto, corresponde al rea debajo de la curva de aceleraci n-tiempo. Por lo tanto, la suma se puede expresar como una integral:
Dado que la aceleración instantanea ($a$) es la derivada de la velocidad ($v$) respecto a el tiempo ($t$),
y la velocidad ($v$) es la derivada de la posición ($s$) respecto a el tiempo ($t$),
tenemos que
$a=\displaystyle\frac{dv}{dt}=\displaystyle\frac{d}{dt}\displaystyle\frac{ds}{dt}=\displaystyle\frac{d^2s}{dt^2}$
por lo tanto,
Ejemplos
Por un lado, es importante diferenciar entre el caso m s simple, unidimensional, y aquel de m s de una dimensi n. Para ambos casos, la derivada de la velocidad ($v$) respecto a el tiempo ($t$), que corresponde a la pendiente de la curva de la velocidad ($v$), es igual a la aceleración instantanea ($a$). De manera similar, la derivada de la velocidad (vector) ($\vec{v}$) respecto a el tiempo ($t$), que corresponde a la velocidad (vector) ($\vec{v}$).
La aceleraci n se define como la variaci n de la velocidad por unidad de tiempo. Sin embargo, esta definici n se refiere a la aceleraci n media que existe durante un intervalo de tiempo dado.
Esta limitaci n de la aceleraci n media se refleja en situaciones donde un objeto acelera para luego frenar y detenerse. En este caso, la aceleraci n media es cero, lo que sugiere que el objeto no ha acelerado en absoluto. Sin embargo, esto no es cierto ya que el objeto se mueve tanto en la fase de aceleraci n como en la de frenado.
Para conocer la aceleraci n en cada instante, se debe considerar un intervalo de tiempo suficientemente peque o, de modo que durante ese tiempo la aceleraci n se pueda considerar aproximadamente constante. De esta manera, la aceleraci n media estimada de esta forma equivale a la aceleraci n existente en el instante considerado.
Por lo tanto, se utiliza el t rmino 'aceleraci n instant nea' para referirse a la aceleraci n en un momento determinado.
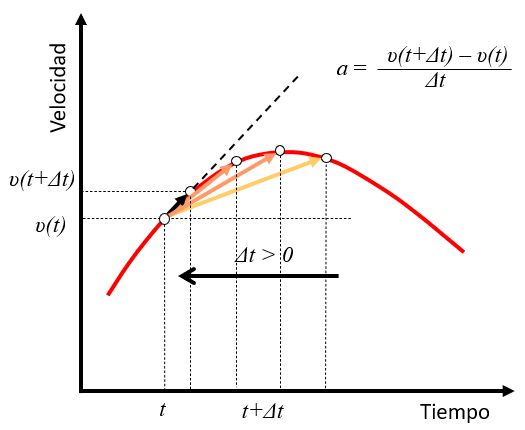
Si tomamos el tiempo transcurrido ($\Delta t$) y observamos un objeto en movimiento con la velocidad ($v$), y luego observamos el mismo objeto en un momento posterior $t+\Delta t$ con velocidad $v(t+\Delta t)$, podemos estimar su aceleraci n como el cambio en la velocidad durante el tiempo transcurrido ($\Delta t$):
$a\sim\displaystyle\frac{v(t+\Delta t)-v(t)}{\Delta t}$
A medida que el valor de $\Delta t$ disminuye, esta expresi n para la aceleraci n se acerca a la tasa de cambio instant nea de la velocidad en el tiempo $t$, o en otras palabras, la pendiente de la recta tangente a la curva de velocidad en ese punto:
Esto generaliza el concepto de la aceleración instantanea ($a$) para el caso de la aceleración constante ($a_0$), como se ha visto anteriormente, expres ndose como la derivada de la velocidad ($v$) respecto a el tiempo ($t$):
Si observamos que la velocidad ($v$) es igual a la distancia recorrida en un tiempo ($\Delta s$) por el tiempo transcurrido ($\Delta t$), indicamos que el desplazamiento es
$\Delta s = v\Delta t$
Como el producto $v\Delta t$ es el rea bajo la curva velocidad versus tiempo y esto, por otro lado, es igual al desplazamiento recorrido:
Esta rea tambi n se puede calcular con la integral de la funci n correspondiente. Por lo tanto, la integral de la aceleraci n entre el tiempo inicial ($t_0$) y el tiempo ($t$) corresponde a la variaci n de la velocidad entre la velocidad inicial la velocidad inicial ($v_0$) y la velocidad ($v$):
La aceleración instantanea ($a$) es igual a la derivada de la velocidad ($v$) en el tiempo ($t$):
Y dado que la velocidad ($v$) es la derivada de la posición ($s$) en el tiempo ($t$):
Entonces, la aceleración instantanea ($a$) es la segunda derivada de la posición ($s$) en el tiempo ($t$),
lo que corresponde a la curvatura de la curva la posición ($s$) en funci n de el tiempo ($t$):
En el caso de una dimensi n, la aceleración instantanea ($a$) est relacionada con la velocidad ($v$) a trav s de su derivada en el tiempo ($t$), mientras que la integral de la aceleración instantanea ($a$) en el intervalo de el tiempo ($t$) a el tiempo inicial ($t_0$) proporciona la velocidad ($v$) desde la velocidad inicial ($v_0$). En un contexto m s general, en m s de una dimensi n, la funci n de la velocidad (vector) ($\vec{v}$) puede ser derivada en el tiempo ($t$), lo que resulta en la velocidad (vector) ($\vec{v}$).
La variable la aceleración media ($\bar{a}$), calculada como el cambio en la diferencia de velocidad ($\Delta v$) dividido por el intervalo de el tiempo transcurrido ($\Delta t$) mediante
es una aproximaci n de la aceleraci n real, que tiende a distorsionarse cuando la aceleraci n fluct a durante el intervalo de tiempo. Por lo tanto, se introduce el concepto de la aceleración instantanea ($a$) determinado en un intervalo de tiempo muy peque o. En este caso, nos referimos a un intervalo de tiempo infinitesimalmente peque o y la variaci n de la velocidad en el tiempo se reduce a la derivada de la velocidad ($v$) respecto a el tiempo ($t$):
lo que corresponde a la derivada de la velocidad.
Si la aceleración instantanea ($a$) corresponde a la derivada de la velocidad ($v$) en el tiempo ($t$),
entonces la velocidad ($v$) es igual a la velocidad inicial ($v_0$), y la integraci n de la aceleraci n desde el tiempo inicial ($t_0$) hasta el tiempo ($t$) es:
Dado que la aceleración instantanea ($a$) es la pendiente de la velocidad ($v$) en funci n de el tiempo ($t$),
y la velocidad ($v$) es la pendiente de la posición ($s$) en funci n de el tiempo ($t$),
podemos expresar la aceleración instantanea ($a$) como la segunda derivada de la posición ($s$) con respecto a el tiempo ($t$).
En general, la velocidad debe entenderse como un vector tridimensional. Es decir, su la posición ($s$) requiere ser descrita por un vector una posición (vector) ($\vec{s}$), para el cual se puede definir cada componente la velocidad ($v$) como se muestra en la siguiente ecuaci n:
Esto permite generalizar la velocidad (vector) ($\vec{v}$) de la siguiente manera:
ID:(1433, 0)