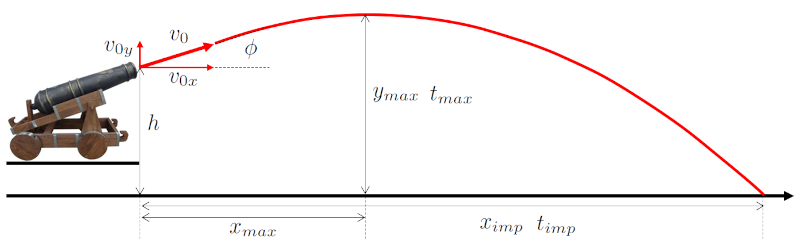
Trayectoria balística
Storyboard 
Si se arroja o dispara un objeto en un campo gravitacional, este realizará dos tipos de movimiento:
• En el eje vertical, se desplazará debido al efecto de la gravedad, lo que significa que estará sometido a la aceleración gravitacional. Para trayectorias de baja altura, esta aceleración puede considerarse constante.
• En el eje horizontal, siempre y cuando se ignore la resistencia del aire, el objeto se desplazará a una velocidad constante, ya que no existe una fuerza que lo acelere o frene.
El resultado es lo que se conoce como una trayectoria balística, que alcanza su distancia máxima cuando se arroja o dispara bajo un ángulo de 45 grados.
ID:(1446, 0)
Trayectoria balística
Storyboard 
Si se arroja o dispara un objeto en un campo gravitacional, este realizará dos tipos de movimiento: • En el eje vertical, se desplazará debido al efecto de la gravedad, lo que significa que estará sometido a la aceleración gravitacional. Para trayectorias de baja altura, esta aceleración puede considerarse constante. • En el eje horizontal, siempre y cuando se ignore la resistencia del aire, el objeto se desplazará a una velocidad constante, ya que no existe una fuerza que lo acelere o frene. El resultado es lo que se conoce como una trayectoria balística, que alcanza su distancia máxima cuando se arroja o dispara bajo un ángulo de 45 grados.
Variables
Cálculos
Cálculos
Ecuaciones
La posición ($s$) recorrido con ERROR:8173,0 con la posición inicial ($s_0$), el tiempo ($t$) y el tiempo inicial ($t_0$) es
Por lo tanto, si el movimiento se inicia en el origen ($s_0=0$) al comienzo del tiempo ($t_0=0$), el movimiento se describe con $x=s$ y $v_0=v_{0x}$.
Para el caso en el que ERROR:5297,0 sea igual a la aceleraci n gravitacional ($a_0=-g$), la trayectoria vertical se puede calcular utilizando la ecuaci n para la posición ($s$) con la posición inicial ($s_0$), la velocidad inicial ($v_0$), el tiempo ($t$) y el tiempo inicial ($t_0$):
En el caso en que el movimiento comience en la altura en que se dispara ($h$) ($s_0=h$), el tiempo inicial ($t_0$) ($t_0=0$) y la velocidad vertical inicial ($v_{0y}$) ($v_0=v_{0y}$) est n dados, el movimiento se puede describir mediante la f rmula:
Para determinar el tiempo de impacto, podemos utilizar la ecuaci n de la posición en el eje y ($y$), que depende de la altura en que se dispara ($h$), la velocidad vertical inicial ($v_{0y}$), la aceleración gravitacional ($g$) y el tiempo ($t$), donde la altura es nula:
Esto resulta en un tiempo:
$t=\displaystyle\frac{ v_{y0} +\sqrt{ v_{0y} ^2 + 2 g h }}{g}$
Con la velocidad inicial ($v_0$) y el angulo en que se dispara ($\phi$):
la tiempo para impacto ($t_{imp}$) es:
Dado que la tiempo para impacto ($t_{imp}$) con la velocidad inicial ($v_0$), el angulo en que se dispara ($\phi$), la aceleración gravitacional ($g$) y la altura en que se dispara ($h$) es
entonces la posición en el eje x ($x$) con la velocidad horizontal inicial ($v_{0x}$) y el tiempo ($t$)
y la velocidad horizontal inicial ($v_{0x}$) con la velocidad inicial ($v_0$) y el angulo en que se dispara ($\phi$)
por lo tanto, obtenemos
La tiempo de máxima altura ($t_{max}$) se alcanza cuando la posición en el eje y ($y$) alcanza un valor m ximo. Esta altura puede calcularse con la altura en que se dispara ($h$), la velocidad vertical inicial ($v_{0y}$), la aceleración gravitacional ($g$) y el tiempo ($t$),
cuya derivada respecto al tiempo es nula en el m ximo, lo que implica:
$\displaystyle\frac{dy}{dt}=v_{0,y}-gt=0$
Por lo tanto, con la expresi n para la velocidad inicial ($v_0$),
tenemos que
El altura máxima alcanzada ($y_{max}$) se alcanza en una tiempo de máxima altura ($t_{max}$) con el angulo en que se dispara ($\phi$), la velocidad constante ($v_0$) y la aceleración gravitacional ($g$),
con lo que se puede determinar la posición en el eje y ($y$) con la altura en que se dispara ($h$), la velocidad vertical inicial ($v_{0y}$) y el tiempo ($t$) mediante la ecuaci n
De este modo, con la velocidad vertical inicial ($v_{0y}$),
en el altura máxima alcanzada ($y_{max}$) es
Ejemplos
Durante la Edad Media, al observar el vuelo de una bola de ca n, se dibujaba una curva que mostraba una subida pronunciada seguida de una ca da casi vertical, como se puede ver en la imagen:
Sin embargo, al analizar las ecuaciones de la cinem tica, se sabe que la trayectoria real de la bola de ca n es muy diferente. De hecho, se trata de una par bola que se produce por la combinaci n del movimiento vertical, causado por la gravedad, y del movimiento horizontal, que es constante.
En otras palabras, el tiempo que la bola permanece en el aire est determinado por su movimiento vertical, mientras que la distancia recorrida en direcci n horizontal est determinada por su velocidad horizontal.
La trayectoria bal stica suele adoptar la forma de una par bola invertida con un punto de ERROR:8433,0 y un distancia máxima alcanzada ($x_{imp}$) con la tiempo de máxima altura ($t_{max}$) y la tiempo para impacto ($t_{imp}$):
Nota: En rigor estricto, las componentes deben estimarse en funci n de sus valores al nivel del suelo para determinar con precisi n los par metros de la altura m xima y el punto de impacto.
Si una masa puntual se mueve con una velocidad inicial ($v_0$) y se dispara bajo un angulo en que se dispara ($\phi$) con respecto a la superficie, entonces su ERROR:8427,0 ser igual a:
Si una masa puntual se mueve con una velocidad inicial ($v_0$) y se dispara bajo un angulo en que se dispara ($\phi$) con respecto a la superficie, entonces su ERROR:8428,0 ser igual a:
El objeto recorre en un tiempo ($t$) a una velocidad horizontal inicial ($v_{0x}$) Una posición en el eje x ($x$) igual a
Un objeto despega en el campo terrestre con una velocidad inicial de la aceleración gravitacional ($g$), a una elevaci n de una altura en que se dispara ($h$) y un ngulo de una velocidad vertical inicial ($v_{0y}$). Alcanzar su objetivo en un tiempo ($t$) con una altura de una posición en el eje y ($y$).
Nota: Si se desea que el blanco est en un punto m s alto que el ca n, se debe emplear una elevaci n una altura en que se dispara ($h$) negativa.
Si un objeto se mueve con una velocidad de una velocidad inicial ($v_0$) y es disparado con un ngulo de un angulo en que se dispara ($\phi$) respecto a la superficie, la tiempo para impacto ($t_{imp}$) puede ser calculado usando la aceleración gravitacional ($g$) y la altura en que se dispara ($h$):
Si un objeto se mueve con una velocidad inicial ($v_0$) y es disparado a un angulo en que se dispara ($\phi$) respecto a la superficie, la aceleración gravitacional ($g$) y la altura en que se dispara ($h$) se pueden calcular con la siguiente f rmula:
Si un objeto se mueve con una velocidad de la velocidad inicial ($v_0$) y es disparado con un ngulo de elevaci n de un angulo en que se dispara ($\phi$) con respecto a la superficie, la altura en la que alcanzar su objetivo, ERROR:8433,0, se puede calcular de la siguiente manera:
Si el objetivo se encuentra a una distancia de la velocidad inicial ($v_0$) y se dispara desde una altura de un angulo en que se dispara ($\phi$) con respecto a la superficie, con una velocidad inicial de la aceleración gravitacional ($g$), entonces la altura que alcanzar el altura máxima alcanzada ($y_{max}$) puede calcularse como:
ID:(1446, 0)