Utilisateur:
Composición de Suelos
Storyboard 
Les principaux composants du sol comprennent à la fois du sable grossier et fin, du limon et de l'argile. La proportion de ces trois composants varie en fonction du type de sol. En raison des différences significatives de taille des particules entre ces composants, des espaces appelés pores se forment. Ces pores peuvent contenir ou faciliter l'écoulement de l'eau, ce qui affecte à son tour le contenu en humidité de la partie non saturée du sol.
ID:(363, 0)
Modèle de sol
Image
Les sols présentent une structure de base composée de différentes couches, dont la formation résulte de leur formation initiale et de leur évolution, sous l'influence de facteurs tels que l'érosion et la croissance de la végétation. Bien que l'épaisseur de ces couches puisse varier considérablement, elles présentent des modèles clairs en ce qui concerne leur teneur en matière organique :
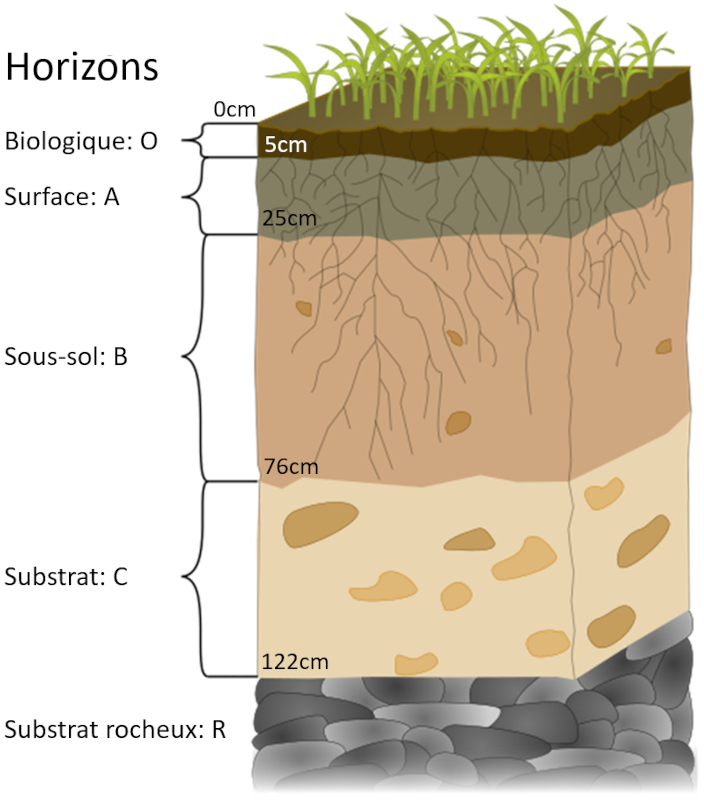
Profil du sol (commons.wikimedia.org - traduit)
O : Couche Organique de Surface
Cette couche provient de l'accumulation de matière organique, principalement composée de matière végétale en décomposition et d'humus. La quantité de matière organique peut atteindre jusqu'à 100 %, en fonction du type de végétation et de son stade de développement.
A : Sol de Surface
Le horizon A se forme grâce à une combinaison d'érosion minérale, d'ajout de matière organique depuis le horizon supérieur et des activités des organismes du sol. La majeure partie de cette couche est composée des composants minéraux inhérents au sol, avec une teneur en matière organique pouvant atteindre 10 %.
B : Sous-sol
Le horizon B accumule des minéraux et des matériaux lessivés qui se déplacent vers le bas à partir du horizon A. Cette accumulation peut également résulter de l'arrivée de minéraux transportés depuis d'autres zones et de processus chimiques se produisant à l'intérieur du horizon. Dans cette couche, la majorité des composants sont des minéraux du sol, avec une teneur en matière organique pouvant atteindre 5 %.
C : Substrat
Le horizon C est principalement formé en raison de processus géologiques et contribue à la configuration générale du terrain. Il fournit des matériaux qui interagissent avec les couches supérieures. Dans cette couche, la plupart des composants sont des minéraux du sol, avec une teneur en matière organique pouvant atteindre 1 %.
L'épaisseur des deux premières couches peut varier de quelques centimètres à plusieurs dizaines de centimètres, tandis que les couches suivantes peuvent s'étendre de dizaines de centimètres à des mètres. Il est important de noter que les valeurs d'épaisseur mentionnées dans l'image de Wikipédia sont fournies uniquement à titre d'exemples illustratifs et peuvent varier largement dans la réalité.
ID:(15066, 0)
Utiliser des tamis pour séparer les composants
Concept
Le sol est composé de proportions variables de sable, de limon et d'argile. Par conséquent, pour modéliser avec précision le comportement du sol, il est nécessaire de représenter sa structure comme un mélange de ces composants.
La manière la plus simple de déterminer la composition d'un échantillon particulier est de calculer la masse de chaque composant par rapport à la masse totale. Pour ce faire, il est nécessaire de séparer physiquement chaque échantillon en ses composants individuels, en exploitant les différences de taille des particules. Après avoir séché et broyé le sol, un processus de tamisage est effectué à l'aide de plusieurs tamis de tailles différentes, choisis en fonction de la précision requise :
L'image illustre un schéma qui sépare trois composants, qui pourraient correspondre à des mesures de sable, de limon et d'argile. Cependant, il est possible d'utiliser plusieurs tamis pour différencier, par exemple, du sable grossier, du sable moyen et du sable fin, selon les besoins.
Les principales masses sont les suivantes :
• a masse sèche de sable dans l'échantillon ($M_a$) : Masse de tous les grains de sable.
• a masse sèche de limon dans l'échantillon ($M_i$) : Masse de tous les grains de limon.
• a masse sèche d'argile dans l'échantillon ($M_c$) : Masse de tous les grains d'argile.
ID:(2067, 0)
Mélanger du sable, du limon et de l'argile
Concept
Un diagramme ternaire est une représentation graphique utilisée pour afficher les proportions relatives de trois composants, tels que le limon, le sable et l'argile. Dans ce diagramme, chaque coin est dédié à l'un de ces composants, et divers points à l'intérieur de l'espace triangulaire représentent des combinaisons uniques de ces constituants.
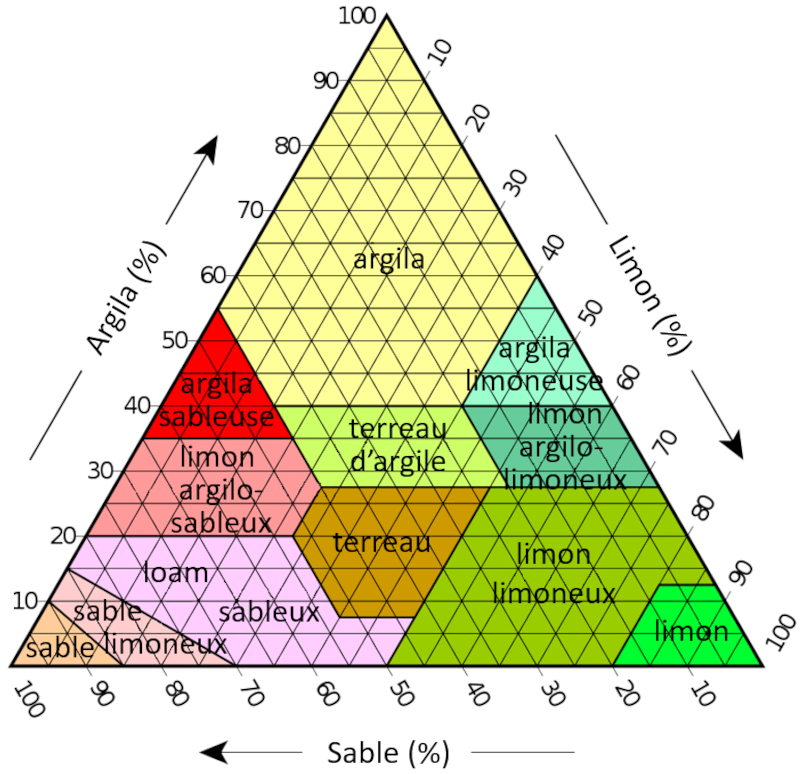
Pour interpréter un diagramme ternaire pour le limon, le sable et l'argile :
1. Identifiez les emplacements des composants :
- Le sable se trouve généralement dans le coin inférieur gauche.
- Le limon est situé dans le coin inférieur droit.
- L'argile se trouve dans le coin supérieur.
2. Analysez les mélanges :
- Les points à l'intérieur du triangle représentent différentes combinaisons de ces trois composants.
3. Comprenez les lignes et les zones :
- Les lignes traversant le triangle représentent des ratios constants des trois composants.
- Différentes régions à l'intérieur du triangle correspondent à des classifications spécifiques des sols.
En particulier, pour les zones spécifiées, les fourchettes suivantes peuvent être estimées :
| Tapez | $g_a$ | $g_i$ | $g_c$ |
| Argile | 0-45 | 0-40 | 55-100 |
| Limon | 23-53 | 28-50 | 40-60 |
| Sable | 85-100 | 0-15 | 0-10 |
| Silt | 0-20 | 87-100 | 0-12 |
| Argile limoneuse | 70-90 | 0-35 | 0-15 |
| Argile sableuse | 45-80 | 0-28 | 20-35 |
| Argile limoneuse sableuse | 45-65 | 0-20 | 35-55 |
| Argile limoneuse silteuse | 0-50 | 50-87 | 0-27 |
| Argile sableuse silteuse | 0-20 | 40-72 | 28-40 |
| Limoneux | 0-20 | 40-60 | 40-60 |
| Sable limoneux | 20-45 | 15-53 | 28-40 |
| Sable loameux | 45-85 | 0-50 | 0-20 |
où tout point doit satisfaire à la condition
| $ g_a + g_i + g_c = 1$ |
ID:(2070, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ g_a + g_i + g_c = 1$
g_a + g_i + g_c = 1
$ g_a =\displaystyle\frac{ M_a }{ M_s }$
g_a = M_a / M_s
$ g_c =\displaystyle\frac{ M_c }{ M_s }$
g_c = M_c / M_s
$ g_i =\displaystyle\frac{ M_i }{ M_s }$
g_i = M_i / M_s
$ M_s = M_a + M_l + M_c $
M_s = M_a + M_l + M_c
$ N_a = \displaystyle\frac{ M_a }{ m_a }$
N_a = M_a / m_a
$ N_c = \displaystyle\frac{ M_c }{ m_c }$
N_c = M_c / m_c
$ N_i = \displaystyle\frac{ M_i }{ m_i }$
N_i = M_i / m_i
$ \rho_p = \rho_a g_a + \rho_i g_i + \rho_c g_c $
rho_p = rho_a * g_a + rho_i * g_i + rho_c * g_c
$ \rho_s = \displaystyle\frac{ M_s }{ V_s }$
rho_s = M_s / V_s
$ V_a =\displaystyle\frac{ M_a }{ \rho_a }$
V_a = M_a / rho_a
$ V_a = N_a v_a $
V_a = N_a * v_a
$ V_c =\displaystyle\frac{ M_c }{ \rho_c }$
V_c = M_c / rho_c
$ V_c = N_c v_c $
V_c = N_c * v_c
$ V_i =\displaystyle\frac{ M_i }{ \rho_i }$
V_i = M_i / rho_i
$ V_i = N_i v_i $
V_i = N_i * v_i
$ V_s = V_a + V_l + V_c $
V_s = V_a + V_l + V_c
$\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$
1/ rho_s = g_a / rho_a + g_i / rho_i + g_c / rho_c
ID:(15216, 0)
Masse sèche totale de l'échantillon
Équation
Pendant l'analyse d'un échantillon, la première étape consiste à éliminer l'eau contenue pour éviter son influence. De cette manière, nous obtenons a masse sèche totale de l'échantillon ($M_s$), qui correspond à la somme de a masse sèche de sable dans l'échantillon ($M_a$), a masse sèche de limon dans l'échantillon ($M_i$) et a masse sèche d'argile dans l'échantillon ($M_c$) :
| $ M_s = M_a + M_l + M_c $ |
Il est important de souligner que cette masse doit être complètement sèche, car l'humidité peut déformer le poids de chaque composant. De plus, tout composant tel que des roches et de la matière organique autres que le sable, le limon ou l'argile doit être retiré de l'échantillon.
ID:(4729, 0)
Fraction de sable dans l'échantillon
Équation
Pour décrire le modèle du sol, nous devons d'abord comprendre sa composition. Pour ce faire, nous introduisons la variable qui représente a fraction massique de sable dans l'échantillon ($g_a$). Cette fraction est calculée à partir de a masse sèche de sable dans l'échantillon ($M_a$) et a masse sèche totale de l'échantillon ($M_s$), en utilisant la relation suivante :
| $ M_s = M_a + M_l + M_c $ |
Cette relation s'exprime comme suit :
| $ g_a =\displaystyle\frac{ M_a }{ M_s }$ |
ID:(4716, 0)
Fraction de limon dans l'échantillon
Équation
Pour décrire le modèle du sol, nous devons d'abord comprendre sa composition. Pour ce faire, nous introduisons la variable qui représente a fraction massique de limon dans l'échantillon ($g_i$). Cette fraction est calculée à partir de a masse sèche de limon dans l'échantillon ($M_i$) et a masse sèche totale de l'échantillon ($M_s$), en utilisant la relation suivante :
| $ M_s = M_a + M_l + M_c $ |
Cette relation s'exprime comme suit :
| $ g_i =\displaystyle\frac{ M_i }{ M_s }$ |
ID:(15064, 0)
Fraction d'argile dans l'échantillon
Équation
Pour décrire le modèle du sol, nous devons d'abord comprendre sa composition. Pour ce faire, nous introduisons la variable qui représente a fraction massique d'argile dans l'échantillon ($g_c$). Cette fraction est calculée à partir de a masse sèche d'argile dans l'échantillon ($M_c$) et a masse sèche totale de l'échantillon ($M_s$), en utilisant la relation suivante :
| $ M_s = M_a + M_l + M_c $ |
Cette relation s'exprime comme suit :
| $ g_c =\displaystyle\frac{ M_c }{ M_s }$ |
ID:(15065, 0)
Condition de normalisation
Équation
Étant donné que les a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$) sont calculés en fonction de leur proportion par rapport aux masses respectives de a masse sèche de sable dans l'échantillon ($M_a$), a masse sèche de limon dans l'échantillon ($M_i$) et a masse sèche d'argile dans l'échantillon ($M_c$) dans l'échantillon, qui se cumulent pour atteindre a masse totale ($M_t$) pour la normalisation :
| $ M_s = M_a + M_l + M_c $ |
Nous obtenons une condition de normalisation :
| $ g_a + g_i + g_c = 1$ |
Lorsque nous ajoutons a fraction massique de sable dans l'échantillon ($g_a$) dans l'échantillon:
| $ g_a =\displaystyle\frac{ M_a }{ M_s }$ |
ainsi que a fraction massique de limon dans l'échantillon ($g_i$) dans l'échantillon :
| $ g_i =\displaystyle\frac{ M_i }{ M_s }$ |
et a fraction massique d'argile dans l'échantillon ($g_c$) dans l'échantillon :
| $ g_c =\displaystyle\frac{ M_c }{ M_s }$ |
nous obtenons :
$g_a + g_i + g_c = \displaystyle\frac{M_a}{M_t} + \displaystyle\frac{M_i}{M_t} + \displaystyle\frac{M_c}{M_t} = \displaystyle\frac{M_a + M_i + M_c}{M_t}$
Étant donné que $M_t$ représente la masse totale, conformément à la condition :
| $ M_s = M_a + M_l + M_c $ |
cela entraîne :
| $ g_a + g_i + g_c = 1$ |
ID:(15072, 0)
Nombre de grains de sable dans l'échantillon
Équation
Pour modéliser le sol, il est important d'introduire la variable correspondante à Le nombre de grains de sable dans l'échantillon ($N_a$), qui peut être calculée en divisant a masse sèche de sable dans l'échantillon ($M_a$) par a masse d'un grain de sable ($m_a$):
| $ N_a = \displaystyle\frac{ M_a }{ m_a }$ |
ID:(1539, 0)
Nombre de grains de limon dans l'échantillon
Équation
Pour modéliser le sol, il est essentiel d'introduire la variable correspondante à Le nombre de grains de limon dans l'échantillon ($N_i$), qui peut être calculée en divisant a masse sèche de limon dans l'échantillon ($M_i$) par a masse d'un grain de limon ($m_i$) :
| $ N_i = \displaystyle\frac{ M_i }{ m_i }$ |
ID:(15067, 0)
Nombre de grains d'argile dans l'échantillon
Équation
Pour modéliser le sol, il est essentiel d'introduire la variable correspondante à Le nombre de grains d'argile dans l'échantillon ($N_c$), qui peut être calculée en divisant a masse sèche d'argile dans l'échantillon ($M_c$) par a masse d'une plaque d'argile ($m_c$) :
| $ N_c = \displaystyle\frac{ M_c }{ m_c }$ |
ID:(15068, 0)
Volume du composant sable de l'échantillon
Équation
Pour modéliser le comportement du sol, il est nécessaire d'introduire la variable correspondante à Le volume solide de sable ($V_a$). Cette variable peut être calculée à partir de le nombre de grains de sable dans l'échantillon ($N_a$) et le volume d'un grain de sable ($v_a$) à l'aide de l'équation suivante :
| $ V_a = N_a v_a $ |
Si nous modélisons le grain comme une sphère avec un rayon $r_a$, nous pouvons calculer son volume à l'aide de la formule suivante :
| $ v_a =\displaystyle\frac{4 \pi }{3} r_a ^3$ |
Avec la densité du sable notée $\rho_a$, nous pouvons déterminer la masse d'un seul grain de sable à l'aide de l'équation suivante :
| $ m_a = \rho_a v_a $ |
En divisant la masse du composant de sable de l'échantillon $M_a$ par la masse d'un seul grain, nous pouvons trouver le nombre de grains :
| $ N_a = \displaystyle\frac{ M_a }{ m_a }$ |
Cela nous permet de calculer le volume du composant de sable :
| $ V_a = N_a v_a $ |
ID:(10366, 0)
Volume de la composante limoneuse de l'échantillon
Équation
Pour modéliser le comportement du sol, il est nécessaire d'introduire la variable correspondante à Le volume solide de limon ($V_i$). Cette variable peut être calculée à partir de le nombre de grains de limon dans l'échantillon ($N_i$) et le volume d'un grain de limon ($v_i$) à l'aide de l'équation suivante :
| $ V_i = N_i v_i $ |
Si nous modélisons le grain comme une sphère avec un rayon de $r_i$, nous pouvons calculer son volume à l'aide de la formule suivante :
| $ v_i = a_i ^3$ |
Avec la densité du limon notée $\rho_i$, nous pouvons déterminer la masse d'un seul grain de limon à l'aide de l'équation suivante :
| $ m_i = \rho_i v_i $ |
En divisant la masse de l'échantillon de limon $M_i$ par la masse d'un seul grain, nous pouvons obtenir le nombre de grains :
| $ V_c = N_c v_c $ |
Cela nous permet de calculer le volume du composant de limon :
| $ V_i = N_i v_i $ |
ID:(10365, 0)
Volume du composant argileux de l'échantillon
Équation
Pour modéliser le comportement du sol, il est nécessaire d'introduire la variable correspondante à Le volume solide d'argile ($V_c$). Cette variable peut être calculée à partir de le nombre de grains d'argile dans l'échantillon ($N_c$) et le volume d'un grain d'argile ($v_c$) à l'aide de l'équation suivante :
| $ V_c = N_c v_c $ |
Si nous modélisons le grain comme une mince plaque avec une longueur et une largeur $l_c$ et une hauteur $w_c$, nous pouvons calculer son volume à l'aide de la formule suivante :
| $ v_c = w_c l_c ^2$ |
Avec la densité de l'argile notée $\rho_c$, nous pouvons déterminer la masse d'un seul grain d'argile à l'aide de l'équation suivante :
| $ m_c = \rho_c v_c $ |
En divisant la masse de l'échantillon d'argile $M_c$ par la masse d'un seul grain, nous pouvons obtenir le nombre de grains :
| $ N_c = \displaystyle\frac{ M_c }{ m_c }$ |
Cela nous permet de calculer le volume du composant d'argile :
| $ V_c = N_c v_c $ |
ID:(15069, 0)
Calcul direct du volume de sable de l'échantillon
Équation
En utilisant la définition de la densité, il est possible de calculer directement le le volume solide de sable ($V_a$) à partir de la a masse sèche de sable dans l'échantillon ($M_a$) et du a densité d'un grain de sable ($\rho_a$) en utilisant la formule suivante :
| $ V_a =\displaystyle\frac{ M_a }{ \rho_a }$ |
Le calcul direct présente l'avantage de ne pas dépendre de la forme des grains :
Si nous supposons que la densité est homogène, nous pouvons calculer le volume total indépendamment du nombre et de la forme des grains.
ID:(3168, 0)
Calcul direct du volume de limon de l'échantillon
Équation
En utilisant la définition de la densité, il est possible de calculer directement le le volume solide de limon ($V_i$) à partir de la a masse sèche de limon dans l'échantillon ($M_i$) et du a densité d'un grain de limon ($\rho_i$) en utilisant la formule suivante :
| $ V_i =\displaystyle\frac{ M_i }{ \rho_i }$ |
Ce calcul direct présente l'avantage de ne pas dépendre de la forme des grains :
Si nous supposons que la densité est homogène, nous pouvons calculer le volume total indépendamment du nombre et de la forme des grains.
ID:(15070, 0)
Calcul direct du volume d'argile de l'échantillon
Équation
En utilisant la définition de la densité, il est possible de calculer directement le le volume solide d'argile ($V_c$) à partir de la a masse sèche d'argile dans l'échantillon ($M_c$) et du a longueur et largeur d'une plaque d'argile ($\rho_c$) en utilisant la formule suivante :
| $ V_c =\displaystyle\frac{ M_c }{ \rho_c }$ |
Ce calcul direct présente l'avantage de ne pas dépendre de la forme des grains :
Si nous supposons que la densité est homogène, nous pouvons calculer le volume total indépendamment du nombre et de la forme des grains.
ID:(15071, 0)
Volume solide de composants
Équation
Une fois que nous connaissons ($$), ($$) et ($$), nous pouvons déterminer le volume solide d'un composant ($V_s$) en additionnant les différentes composantes, comme décrit dans l'équation suivante :
| $ V_s = V_a + V_l + V_c $ |
ID:(4734, 0)
Densité solide
Équation
Puisque nous connaissons déjà A masse sèche totale de l'échantillon ($M_s$) et le volume solide ($V_s$) à partir de l'échantillon, nous pouvons introduire a densité solide ($\rho_s$) et le calculer à l'aide de l'équation suivante :
| $ \rho_s = \displaystyle\frac{ M_s }{ V_s }$ |
ID:(15073, 0)
Calcul de la densité solide à partir de fractions
Équation
A densité solide ($\rho_s$) peut être calculé à partir de a densité d'un grain de sable ($\rho_a$), a densité d'un grain de limon ($\rho_i$) et a longueur et largeur d'une plaque d'argile ($\rho_c$), ainsi que des facteurs décrivant sa composition : a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$). Cela nous conduit à la relation suivante :
| $\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$ |
Si nous exprimons l'inverse de a densité solide ($\rho_s$) défini dans a masse sèche totale de l'échantillon ($M_s$) et le volume solide ($V_s$) à l'aide de l'équation suivante :
| $ \rho_s = \displaystyle\frac{ M_s }{ V_s }$ |
Et en tenant compte du fait que le volume solide est la somme de le volume solide de sable ($V_a$), le volume solide de limon ($V_i$) et le volume solide d'argile ($V_c$) :
| $ V_s = V_a + V_l + V_c $ |
Nous obtenons :
$\displaystyle\frac{1}{\rho_s}=\displaystyle\frac{V_s}{M_s}=\displaystyle\frac{V_a+V_i+V_c}{M_s}$
En remplaçant les volumes par les relations pour a densité d'un grain de sable ($\rho_a$)
| $ V_a =\displaystyle\frac{ M_a }{ \rho_a }$ |
pour a densité d'un grain de limon ($\rho_i$)
| $ V_i =\displaystyle\frac{ M_i }{ \rho_i }$ |
et a longueur et largeur d'une plaque d'argile ($\rho_c$)
| $ V_c =\displaystyle\frac{ M_c }{ \rho_c }$ |
Nous obtenons :
$\displaystyle\frac{1}{\rho_s}=\displaystyle\frac{1}{\rho_a}\displaystyle\frac{M_a}{M_s}+\displaystyle\frac{1}{\rho_i}\displaystyle\frac{M_i}{M_s}+\displaystyle\frac{1}{\rho_c}\displaystyle\frac{M_c}{M_s}$
Avec a fraction massique de sable dans l'échantillon ($g_a$)
| $ g_a =\displaystyle\frac{ M_a }{ M_s }$ |
pour a fraction massique de limon dans l'échantillon ($g_i$)
| $ g_i =\displaystyle\frac{ M_i }{ M_s }$ |
et a fraction massique d'argile dans l'échantillon ($g_c$)
| $ g_c =\displaystyle\frac{ M_c }{ M_s }$ |
Nous obtenons :
| $\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$ |
ID:(15074, 0)
Densité de particules
Équation
A densité de particules ($\rho_p$) peut être calculé comme la densité moyenne, où les facteurs de pondération sont les composants. Par conséquent, avec a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$), a fraction massique d'argile dans l'échantillon ($g_c$) et a densité d'un grain de sable ($\rho_a$), a densité d'un grain de limon ($\rho_i$), a longueur et largeur d'une plaque d'argile ($\rho_c$), il peut être défini comme suit:
| $ \rho_p = \rho_a g_a + \rho_i g_i + \rho_c g_c $ |
ID:(15127, 0)