Storyboard

Die Hauptbestandteile des Bodens umfassen sowohl groben als auch feinen Sand, Schluff und Ton. Das Verhältnis dieser drei Komponenten variiert je nach Bodenart. Aufgrund signifikanter Unterschiede in der Partikelgröße zwischen diesen Komponenten entstehen Hohlräume, die als Poren bezeichnet werden. Diese Poren können Wasser aufnehmen oder den Fluss von Wasser erleichtern, was wiederum den Feuchtigkeitsgehalt des ungesättigten Teils des Bodens beeinflusst.

>Modell

ID:(363, 0)

Iframe

>Top

ID:(15197, 0)

Bild

>Top

Böden haben eine grundlegende Struktur aus verschiedenen Schichten, die auf ihre anfängliche Bildung und ihre Entwicklung zurückzuführen sind, beeinflusst von Faktoren wie Erosion und Vegetationswachstum. Obwohl die Dicke dieser Schichten erheblich variieren kann, zeigen sie klare Muster in Bezug auf ihren organischen Gehalt:

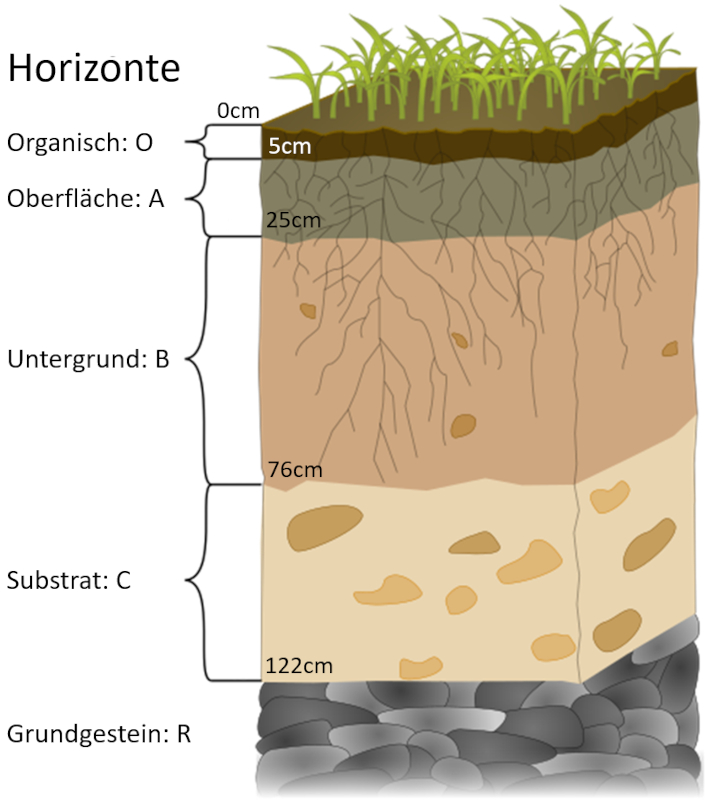
Bodenprofil (commons.wikimedia.org übersetzt)

O: Organische Oberflächenschicht

Diese Schicht entsteht durch die Anhäufung von organischem Material, das hauptsächlich aus sich zersetzendem Pflanzenmaterial und Humus besteht. Die Menge an organischem Material kann je nach Art der Vegetation und ihrem Entwicklungsstadium bis zu 100% erreichen.

A: Oberboden

Der A-Horizont entsteht durch eine Kombination aus mineralischer Erosion, der Zugabe von organischem Material aus dem oberen Horizont und den Aktivitäten von Bodenorganismen. Der Großteil dieser Schicht besteht aus den mineralischen Bestandteilen des Bodens, wobei der organische Anteil bis zu 10% betragen kann.

B: Unterboden

Der B-Horizont akkumuliert Mineralien und aus dem A-Horizont nach unten bewegte lixivierte Materialien. Diese Anreicherung kann auch durch Mineralien erfolgen, die aus anderen Gebieten transportiert werden, und durch chemische Prozesse innerhalb des Horizonts. In dieser Schicht bestehen die meisten Bestandteile aus Bodenmineralien, wobei der organische Anteil bis zu 5% betragen kann.

C: Substrat

Der C-Horizont entsteht hauptsächlich durch geologische Prozesse und trägt zur allgemeinen Geländeform bei. Er stellt Materialien bereit, die mit den oberen Schichten interagieren. In dieser Schicht bestehen die meisten Bestandteile aus Bodenmineralien, wobei der organische Anteil bis zu 1% betragen kann.

Die Dicke der ersten beiden Schichten kann von wenigen Zentimetern bis zu mehreren Dezimetern variieren, während die letzten Schichten von Dezimetern bis zu Metern reichen können. Es ist wichtig zu beachten, dass die in der Wikipedia-Abbildung angegebenen Dickenwerte nur als illustrierende Beispiele dienen und in der Realität erheblich variieren können.

ID:(15066, 0)

Konzept

>Top

Boden besteht aus verschiedenen Anteilen von Sand, Schluff und Ton. Um das Verhalten des Bodens präzise zu modellieren, ist es erforderlich, seine Struktur als eine Mischung dieser Komponenten darzustellen.

Die einfachste Methode, um die Zusammensetzung einer bestimmten Probe zu bestimmen, besteht darin, die Masse jeder Komponente im Verhältnis zur Gesamtmasse zu berechnen. Hierfür ist es notwendig, jede Probe physisch in ihre Einzelkomponenten zu trennen und die Unterschiede in der Partikelgröße zu nutzen. Nach dem Trocknen und Zerkleinern des Bodens wird ein Siebprozess mit mehreren Sieben unterschiedlicher Größe durchgeführt, die je nach erforderlicher Genauigkeit ausgewählt werden:

Das Bild veranschaulicht ein Schema, das drei Komponenten trennt, die Messungen von Sand, Schluff und Ton entsprechen könnten. Es ist jedoch möglich, mehrere Siebe zu verwenden, um beispielsweise groben Sand, mittleren Sand und feinen Sand je nach Bedarf zu unterscheiden.

Die Hauptmassen sind daher:

• die Sandtrockenmasse ($M_a$): Masse aller Sandkörner.
• die Trockene Schlammmasse in der Probe ($M_i$): Masse aller Schluffkörner.
• die Masa seca de arcilla en la muestra ($M_c$): Masse aller Tonkörner.

ID:(2067, 0)

Konzept

>Top

Ein Dreiecksdiagramm, auch Ternärdiagramm genannt, ist eine graphische Darstellung zur Anzeige der Anteile von drei Komponenten wie Schluff, Sand und Ton. Dabei repräsentiert jede Ecke eine dieser drei Komponenten, und verschiedene Punkte innerhalb des Dreiecks stehen für unterschiedliche Kombinationen dieser Bestandteile.

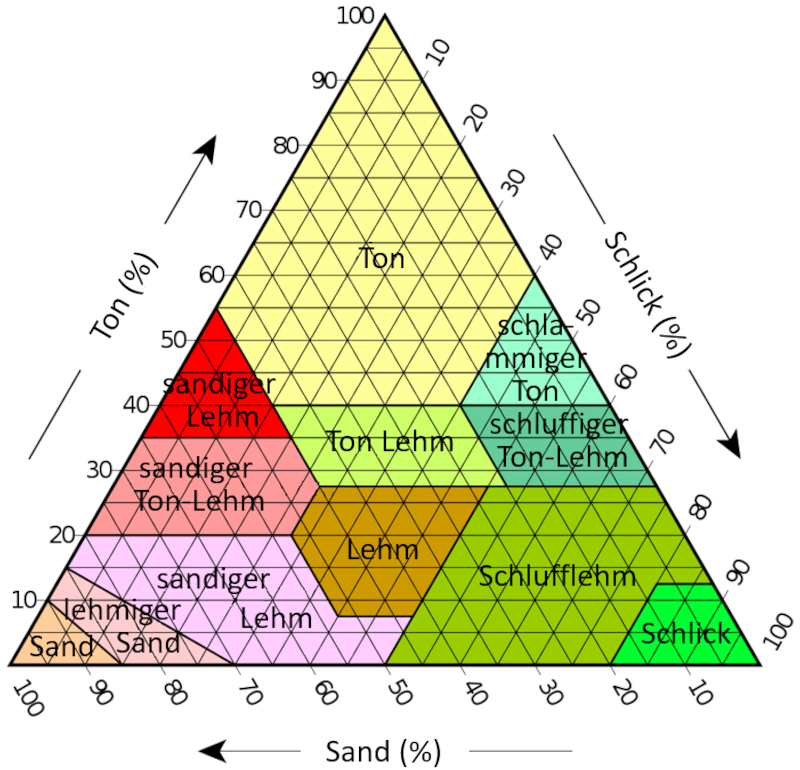
Um ein Ternärdiagramm für Schluff, Sand und Ton zu interpretieren:

1. Identifizieren Sie die Standorte der Komponenten:
- Sand befindet sich in der Regel in der unteren linken Ecke.
- Schluff befindet sich in der unteren rechten Ecke.
- Ton ist oben in der Ecke zu finden.

2. Analysieren Sie die Mischungen:
- Punkte innerhalb des Dreiecks repräsentieren vielfältige Mischungen dieser drei Komponenten.

3. Verstehen Sie Linien und Zonen:
- Linien, die das Dreieck durchqueren, stehen für konstante Verhältnisse der drei Komponenten.
- Unterschiedliche Regionen innerhalb des Dreiecks entsprechen spezifischen Bodenklassifikationen.

Insbesondere können für die angegebenen Zonen folgende Reichweiten abgeschätzt werden:

wobei jeder Punkt die Bedingung erfüllen muss

ID:(2070, 0)

Top

>Top

Parameter

$\rho_a$

rho_a

Dichte eines Sandkorns

kg/m^3

$\rho_i$

rho_i

Dichte eines Schluffkorns

kg/m^3

$\rho_c$

rho_c

Dichte eines Tonkorns

kg/m^3

$\rho_s$

rho_s

Festkörperdichte

kg/m^3

$m_c$

m_c

Masse einer Tonplatte

kg

$m_a$

m_a

Masse eines Sandkorns

kg

$m_i$

m_i

Masse eines Schlickkorns

kg

$\rho_p$

rho_p

Teilchendichte

kg/m^3

$v_a$

v_a

Volumen eines Sandkorns

m^3

$v_i$

v_i

Volumen eines Schlickkorns

m^3

$v_c$

v_c

Volumen eines Tonkorns

m^3

Variablen

$N_a$

N_a

Anzahl der Sandkörner in der Probe

-

$N_i$

N_i

Anzahl der Schluffkörner in der Probe

-

$N_c$

N_c

Anzahl der Tonkörner in der Probe

-

$V_a$

V_a

Festes Sandvolumen

m^3

$V_i$

V_i

Festes Schlammvolumen

m^3

$V_c$

V_c

Festes Tonvolumen

m^3

$M_s$

M_s

Gesamttrockenmasse der Probe

kg

$M_c$

M_c

Masa seca de arcilla en la muestra

kg

$g_a$

g_a

Massenanteil von Sand in der Probe

-

$g_i$

g_i

Massenanteil von Schluff in der Probe

-

$g_c$

g_c

Massenanteil von Ton in der Probe

-

$M_a$

M_a

Sandtrockenmasse

kg

$M_i$

M_i

Trockene Schlammmasse in der Probe

kg

$V_s$

V_s

Volumenkörper einer Komponente

m^3

Berechnungen

• Alternative Methode
• Traditionelle Methode
• Strategie
• 2D
• 3D

Gleichung

Zahl

Zuerst die Gleichung auswählen: zu , dann die Variable auswählen: zu

---

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable Gegeben Berechnen Ziel : Gleichung Zu verwenden

Gleichungen

ID:(15216, 0)

Gleichung

>Top, >Modell

Während der Analyse einer Probe besteht der erste Schritt darin, das enthaltene Wasser zu entfernen, um seinen Einfluss zu verhindern. Auf diese Weise erhalten wir die Gesamttrockenmasse der Probe ($M_s$), das der Summe von die Sandtrockenmasse ($M_a$), die Trockene Schlammmasse in der Probe ($M_i$) und die Masa seca de arcilla en la muestra ($M_c$) entspricht:

$M_s = M_a + M_l + M_c$

Bedingungen

Variablen

$M_s$

Gesamttrockenmasse der Probe

$kg$

5987

$M_c$

Masa seca de arcilla en la muestra

$kg$

6035

$M_a$

Sandtrockenmasse

$kg$

6033

$M_i$

Trockene Schlammmasse in der Probe

$kg$

6034

Beziehung

Es ist wichtig zu betonen, dass diese Masse vollständig trocken sein muss, da Feuchtigkeit das Gewicht jedes Bestandteils verfälschen kann. Darüber hinaus müssen alle Komponenten wie Steine und organisches Material, die nicht Sand, Schluff oder Ton sind, aus der Probe entfernt werden.

ID:(4729, 0)

Gleichung

>Top, >Modell

Um das Bodenmodell zu beschreiben, müssen wir zunächst seine Zusammensetzung verstehen. Dazu führen wir die Variable ein, die die Massenanteil von Sand in der Probe ($g_a$) repräsentiert. Diese Fraktion wird aus die Sandtrockenmasse ($M_a$) und die Gesamttrockenmasse der Probe ($M_s$) berechnet, indem wir die folgende Beziehung verwenden:

Diese Beziehung wird wie folgt ausgedrückt:

$g_a =\displaystyle\frac{ M_a }{ M_s }$

Bedingungen

Variablen

$M_s$

Gesamttrockenmasse der Probe

$kg$

5987

$g_a$

Massenanteil von Sand in der Probe

$-$

5797

$M_a$

Sandtrockenmasse

$kg$

6033

Beziehung

ID:(4716, 0)

Gleichung

>Top, >Modell

Um das Bodenmodell zu beschreiben, müssen wir zunächst seine Zusammensetzung verstehen. Dazu führen wir die Variable ein, die die Massenanteil von Schluff in der Probe ($g_i$) repräsentiert. Diese Fraktion wird aus die Trockene Schlammmasse in der Probe ($M_i$) und die Gesamttrockenmasse der Probe ($M_s$) berechnet, indem wir die folgende Beziehung verwenden:

Diese Beziehung wird wie folgt ausgedrückt:

$g_i =\displaystyle\frac{ M_i }{ M_s }$

Bedingungen

Variablen

$M_s$

Gesamttrockenmasse der Probe

$kg$

5987

$g_i$

Massenanteil von Schluff in der Probe

$-$

10098

$M_i$

Trockene Schlammmasse in der Probe

$kg$

6034

Beziehung

ID:(15064, 0)

Gleichung

>Top, >Modell

Um das Bodenmodell zu beschreiben, müssen wir zunächst seine Zusammensetzung verstehen. Dazu führen wir die Variable ein, die die Massenanteil von Ton in der Probe ($g_c$) repräsentiert. Diese Fraktion wird aus die Masa seca de arcilla en la muestra ($M_c$) und die Gesamttrockenmasse der Probe ($M_s$) berechnet, indem wir die folgende Beziehung verwenden:

Diese Beziehung wird wie folgt ausgedrückt:

$g_c =\displaystyle\frac{ M_c }{ M_s }$

Bedingungen

Variablen

$M_s$

Gesamttrockenmasse der Probe

$kg$

5987

$M_c$

Masa seca de arcilla en la muestra

$kg$

6035

$g_c$

Massenanteil von Ton in der Probe

$-$

10099

Beziehung

ID:(15065, 0)

Gleichung

>Top, >Modell

Da die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$) aufgrund ihres Verhältnisses zu den jeweiligen Massen von die Sandtrockenmasse ($M_a$), die Trockene Schlammmasse in der Probe ($M_i$) und die Masa seca de arcilla en la muestra ($M_c$) in der Probe berechnet werden, die sich auf die Gesamtmasse ($M_t$) zur Normalisierung summieren:

erhalten wir eine Normalisierungsbedingung:

$g_a + g_i + g_c = 1$

Bedingungen

Variablen

$g_a$

Massenanteil von Sand in der Probe

$-$

5797

$g_i$

Massenanteil von Schluff in der Probe

$-$

10098

$g_c$

Massenanteil von Ton in der Probe

$-$

10099

Beziehung

Entwicklung

Wenn wir den die Massenanteil von Sand in der Probe ($g_a$) in der Probe:

$g_a =\displaystyle\frac{ M_a }{ M_s }$

zusammen mit die Massenanteil von Schluff in der Probe ($g_i$) in der Probe:

$g_i =\displaystyle\frac{ M_i }{ M_s }$

und dem die Massenanteil von Ton in der Probe ($g_c$) in der Probe:

$g_c =\displaystyle\frac{ M_c }{ M_s }$

erhalten wir:

$g_a + g_i + g_c = \displaystyle\frac{M_a}{M_t} + \displaystyle\frac{M_i}{M_t} + \displaystyle\frac{M_c}{M_t} = \displaystyle\frac{M_a + M_i + M_c}{M_t}$

Da $M_t$ die Gesamtmasse darstellt, wie in der Bedingung:

$M_s = M_a + M_l + M_c$

angegeben, ergibt sich:

$g_a + g_i + g_c = 1$

ID:(15072, 0)

Gleichung

>Top, >Modell

Um den Boden zu modellieren, ist es wichtig, die Variable einzuführen, die der Anzahl der Sandkörner in der Probe ($N_a$) entspricht, die durch Division von die Sandtrockenmasse ($M_a$) durch die Masse eines Sandkorns ($m_a$) berechnet werden kann:

$N_a = \displaystyle\frac{ M_a }{ m_a }$

Bedingungen

Variablen

$N_a$

Anzahl der Sandkörner in der Probe

$-$

4941

$m_a$

Masse eines Sandkorns

$kg$

4942

$M_a$

Sandtrockenmasse

$kg$

6033

Beziehung

ID:(1539, 0)

Gleichung

>Top, >Modell

Um den Boden zu modellieren, ist es entscheidend, die Variable einzuführen, die der Anzahl der Schluffkörner in der Probe ($N_i$) entspricht, die durch Division von die Trockene Schlammmasse in der Probe ($M_i$) durch die Masse eines Schlickkorns ($m_i$) berechnet werden kann:

$N_i = \displaystyle\frac{ M_i }{ m_i }$

Bedingungen

Variablen

$N_i$

Anzahl der Schluffkörner in der Probe

$-$

10100

$m_i$

Masse eines Schlickkorns

$kg$

5988

$M_i$

Trockene Schlammmasse in der Probe

$kg$

6034

Beziehung

ID:(15067, 0)

Gleichung

>Top, >Modell

Um den Boden zu modellieren, ist es entscheidend, die Variable einzuführen, die der Anzahl der Tonkörner in der Probe ($N_c$) entspricht, die durch Division von die Masa seca de arcilla en la muestra ($M_c$) durch die Masse einer Tonplatte ($m_c$) berechnet werden kann:

$N_c = \displaystyle\frac{ M_c }{ m_c }$

Bedingungen

Variablen

$N_c$

Anzahl der Tonkörner in der Probe

$-$

10101

$M_c$

Masa seca de arcilla en la muestra

$kg$

6035

$m_c$

Masse einer Tonplatte

$kg$

6278

Beziehung

ID:(15068, 0)

Gleichung

>Top, >Modell

Um das Verhalten des Bodens zu modellieren, ist es notwendig, die Variable einzuführen, die das Festes Sandvolumen ($V_a$) entspricht. Diese Variable kann aus der Anzahl der Sandkörner in der Probe ($N_a$) und der Volumen eines Sandkorns ($v_a$) mithilfe der folgenden Gleichung berechnet werden:

$V_a = N_a v_a$

Bedingungen

Variablen

$N_a$

Anzahl der Sandkörner in der Probe

$-$

4941

$V_a$

Festes Sandvolumen

$m^3$

6554

$v_a$

Volumen eines Sandkorns

$m^3$

5798

Beziehung

Entwicklung

Wenn wir das Korn als eine Kugel mit einem Radius von $r_a$ modellieren, können wir sein Volumen mithilfe der Formel berechnen:

$v_a =\displaystyle\frac{4 \pi }{3} r_a ^3$

Mit der Dichte des Sandes, die als $\rho_a$ bezeichnet wird, können wir die Masse eines einzelnen Sandkorns mithilfe der folgenden Gleichung bestimmen:

$m_a = \rho_a v_a$

Durch die Teilung der Masse der Sandkomponente der Probe $M_a$ durch die Masse eines einzelnen Korns können wir die Anzahl der Körner ermitteln:

$N_a = \displaystyle\frac{ M_a }{ m_a }$

Dies ermöglicht es uns, das Volumen der Sandkomponente zu berechnen:

$V_a = N_a v_a$

ID:(10366, 0)

Gleichung

>Top, >Modell

Um das Verhalten des Bodens zu modellieren, ist es notwendig, die Variable einzuführen, die das Festes Schlammvolumen ($V_i$) entspricht. Diese Variable kann aus der Anzahl der Schluffkörner in der Probe ($N_i$) und der Volumen eines Schlickkorns ($v_i$) mithilfe der folgenden Gleichung berechnet werden:

$V_i = N_i v_i$

Bedingungen

Variablen

$N_i$

Anzahl der Schluffkörner in der Probe

$-$

10100

$V_i$

Festes Schlammvolumen

$m^3$

6555

$v_i$

Volumen eines Schlickkorns

$m^3$

4943

Beziehung

Entwicklung

Wenn wir das Korn als eine Kugel mit einem Radius von $r_i$ modellieren, können wir sein Volumen mithilfe der folgenden Formel berechnen:

$v_i = a_i ^3$

Mit der Dichte des Schluffs, die als $\rho_i$ bezeichnet wird, können wir die Masse eines einzelnen Schluffkorns mithilfe der folgenden Gleichung ermitteln:

$m_i = \rho_i v_i$

Durch die Teilung der Masse der Schluffprobe $M_i$ durch die Masse eines einzelnen Korns können wir die Anzahl der Körner ermitteln:

$V_c = N_c v_c$

Dies ermöglicht es uns, das Volumen der Schluffkomponente zu berechnen:

$V_i = N_i v_i$

ID:(10365, 0)

Gleichung

>Top, >Modell

Um das Verhalten des Bodens zu modellieren, ist es notwendig, die Variable einzuführen, die das Festes Tonvolumen ($V_c$) entspricht. Diese Variable kann aus der Anzahl der Tonkörner in der Probe ($N_c$) und der Volumen eines Tonkorns ($v_c$) mithilfe der folgenden Gleichung berechnet werden:

$V_c = N_c v_c$

Bedingungen

Variablen

$N_c$

Anzahl der Tonkörner in der Probe

$-$

10101

$V_c$

Festes Tonvolumen

$m^3$

6556

$v_c$

Volumen eines Tonkorns

$m^3$

5799

Beziehung

Entwicklung

Wenn wir das Korn als eine dünne Platte mit Länge und Breite $l_c$ und Höhe $w_c$ modellieren, können wir sein Volumen mithilfe der folgenden Formel berechnen:

$v_c = w_c l_c ^2$

Mit der Dichte des Tons, die als $\rho_c$ bezeichnet wird, können wir die Masse eines einzelnen Tonkorns mithilfe der folgenden Gleichung ermitteln:

$m_c = \rho_c v_c$

Durch die Teilung der Masse der Tonprobe $M_c$ durch die Masse eines einzelnen Korns können wir die Anzahl der Körner ermitteln:

$N_c = \displaystyle\frac{ M_c }{ m_c }$

Dies ermöglicht es uns, das Volumen der Tonkomponente zu berechnen:

$V_c = N_c v_c$

ID:(15069, 0)

Gleichung

>Top, >Modell

Mithilfe der Definition der Dichte ist es möglich, das Festes Sandvolumen ($V_a$) direkt aus die Sandtrockenmasse ($M_a$) und die Dichte eines Sandkorns ($\rho_a$) mithilfe der folgenden Formel zu berechnen:

$V_a =\displaystyle\frac{ M_a }{ \rho_a }$

Bedingungen

Variablen

$\rho_a$

Dichte eines Sandkorns

2.63e+3

$kg/m^3$

10095

$V_a$

Festes Sandvolumen

$m^3$

6554

$M_a$

Sandtrockenmasse

$kg$

6033

Beziehung

Die direkte Berechnung hat den Vorteil, dass sie nicht von der Form der Körner abhängt:

Wenn wir annehmen, dass die Dichte homogen ist, können wir das Gesamtvolumen unabhängig von der Anzahl und Form der Körner berechnen.

ID:(3168, 0)

Gleichung

>Top, >Modell

Mit Hilfe der Definition der Dichte ist es möglich, das Festes Schlammvolumen ($V_i$) direkt aus die Trockene Schlammmasse in der Probe ($M_i$) und die Dichte eines Schluffkorns ($\rho_i$) mit Hilfe der folgenden Formel zu berechnen:

$V_i =\displaystyle\frac{ M_i }{ \rho_i }$

Bedingungen

Variablen

$\rho_i$

Dichte eines Schluffkorns

2.65e+3

$kg/m^3$

10094

$V_i$

Festes Schlammvolumen

$m^3$

6555

$M_i$

Trockene Schlammmasse in der Probe

$kg$

6034

Beziehung

Diese direkte Berechnung hat den Vorteil, dass sie nicht von der Form der Körner abhängt:

Wenn wir annehmen, dass die Dichte homogen ist, können wir das Gesamtvolumen unabhängig von der Anzahl und Form der Körner berechnen.

ID:(15070, 0)

Gleichung

>Top, >Modell

Mit Hilfe der Definition der Dichte ist es möglich, das Festes Tonvolumen ($V_c$) direkt aus die Masa seca de arcilla en la muestra ($M_c$) und die Dichte eines Tonkorns ($\rho_c$) mit Hilfe der folgenden Formel zu berechnen:

$V_c =\displaystyle\frac{ M_c }{ \rho_c }$

Bedingungen

Variablen

$\rho_c$

Dichte eines Tonkorns

2.8e+3

$kg/m^3$

10093

$V_c$

Festes Tonvolumen

$m^3$

6556

$M_c$

Masa seca de arcilla en la muestra

$kg$

6035

Beziehung

Diese direkte Berechnung hat den Vorteil, dass sie nicht von der Form der Körner abhängt:

Wenn wir annehmen, dass die Dichte homogen ist, können wir das Gesamtvolumen unabhängig von der Anzahl und Form der Körner berechnen.

ID:(15071, 0)

Gleichung

>Top, >Modell

Sobald wir Elektronenenergie ($E$), Anfällig ($S_t$) und Entzündet ($I_t$) kennen, können wir das Volumenkörper einer Komponente ($V_s$) bestimmen, indem wir die verschiedenen Komponenten summieren, wie in der folgenden Gleichung beschrieben:

$V_s = V_a + V_l + V_c$

Bedingungen

Variablen

$V_a$

Festes Sandvolumen

$m^3$

6554

$V_i$

Festes Schlammvolumen

$m^3$

6555

$V_c$

Festes Tonvolumen

$m^3$

6556

$V_s$

Volumenkörper einer Komponente

$m^3$

6038

Beziehung

ID:(4734, 0)

Gleichung

>Top, >Modell

Da wir bereits die Gesamttrockenmasse der Probe ($M_s$) und das Solides Volumen ($V_s$) aus der Probe kennen, können wir die Festkörperdichte ($\rho_s$) einführen und es mithilfe der folgenden Gleichung berechnen:

$\rho_s = \displaystyle\frac{ M_s }{ V_s }$

Bedingungen

Variablen

$\rho_s$

Festkörperdichte

$kg/m^3$

4944

$M_s$

Gesamttrockenmasse der Probe

$kg$

5987

$V_s$

Volumenkörper einer Komponente

$m^3$

6038

Beziehung

ID:(15073, 0)

Gleichung

>Top, >Modell

Die Festkörperdichte ($\rho_s$) kann aus die Dichte eines Sandkorns ($\rho_a$), die Dichte eines Schluffkorns ($\rho_i$) und die Dichte eines Tonkorns ($\rho_c$) sowie aus den Faktoren, die seine Zusammensetzung beschreiben, berechnet werden: die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$) und die Massenanteil von Ton in der Probe ($g_c$). Dies führt uns zu folgender Beziehung:

$\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$

Bedingungen

Variablen

$\rho_a$

Dichte eines Sandkorns

2.63e+3

$kg/m^3$

10095

$\rho_i$

Dichte eines Schluffkorns

2.65e+3

$kg/m^3$

10094

$\rho_c$

Dichte eines Tonkorns

2.8e+3

$kg/m^3$

10093

$\rho_s$

Festkörperdichte

$kg/m^3$

4944

$g_a$

Massenanteil von Sand in der Probe

$-$

5797

$g_i$

Massenanteil von Schluff in der Probe

$-$

10098

$g_c$

Massenanteil von Ton in der Probe

$-$

10099

Beziehung

Entwicklung

Wenn wir das Inverse von die Festkörperdichte ($\rho_s$), das in die Gesamttrockenmasse der Probe ($M_s$) und das Solides Volumen ($V_s$) definiert ist, mit der folgenden Gleichung ausdrücken:

$\rho_s = \displaystyle\frac{ M_s }{ V_s }$

Und wenn wir berücksichtigen, dass das feste Volumen die Summe aus das Festes Sandvolumen ($V_a$), das Festes Schlammvolumen ($V_i$) und das Festes Tonvolumen ($V_c$) ist:

$V_s = V_a + V_l + V_c$

Erhalten wir:

$\displaystyle\frac{1}{\rho_s}=\displaystyle\frac{V_s}{M_s}=\displaystyle\frac{V_a+V_i+V_c}{M_s}$

Indem wir die Volumina durch die Beziehungen für die Dichte eines Sandkorns ($\rho_a$)

$V_a =\displaystyle\frac{ M_a }{ \rho_a }$

für die Dichte eines Schluffkorns ($\rho_i$)

$V_i =\displaystyle\frac{ M_i }{ \rho_i }$

und die Dichte eines Tonkorns ($\rho_c$)

$V_c =\displaystyle\frac{ M_c }{ \rho_c }$

ersetzen, erhalten wir:

$\displaystyle\frac{1}{\rho_s}=\displaystyle\frac{1}{\rho_a}\displaystyle\frac{M_a}{M_s}+\displaystyle\frac{1}{\rho_i}\displaystyle\frac{M_i}{M_s}+\displaystyle\frac{1}{\rho_c}\displaystyle\frac{M_c}{M_s}$

Mit die Massenanteil von Sand in der Probe ($g_a$)

$g_a =\displaystyle\frac{ M_a }{ M_s }$

für die Massenanteil von Schluff in der Probe ($g_i$)

$g_i =\displaystyle\frac{ M_i }{ M_s }$

und die Massenanteil von Ton in der Probe ($g_c$)

$g_c =\displaystyle\frac{ M_c }{ M_s }$

erhalten wir:

$\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$

ID:(15074, 0)

Gleichung

>Top, >Modell

Die Teilchendichte ($\rho_p$) kann als die Durchschnittsdichte berechnet werden, wobei die Gewichtungsfaktoren die Komponenten sind. Daher kann es mit die Massenanteil von Sand in der Probe ($g_a$), die Massenanteil von Schluff in der Probe ($g_i$), die Massenanteil von Ton in der Probe ($g_c$) und die Dichte eines Sandkorns ($\rho_a$), die Dichte eines Schluffkorns ($\rho_i$), die Dichte eines Tonkorns ($\rho_c$) wie folgt definiert werden:

$\rho_p = \rho_a g_a + \rho_i g_i + \rho_c g_c$

Bedingungen

Variablen

$\rho_a$

Dichte eines Sandkorns

2.63e+3

$kg/m^3$

10095

$\rho_i$

Dichte eines Schluffkorns

2.65e+3

$kg/m^3$

10094

$\rho_c$

Dichte eines Tonkorns

2.8e+3

$kg/m^3$

10093

$g_a$

Massenanteil von Sand in der Probe

$-$

5797

$g_i$

Massenanteil von Schluff in der Probe

$-$

10098

$g_c$

Massenanteil von Ton in der Probe

$-$

10099

$\rho_p$

Teilchendichte

$kg/m^3$

10168

Beziehung

ID:(15127, 0)