Utilisateur:
Indicateurs
Storyboard 
La présence de pores est l'un des aspects clés du comportement du sol. D'une part, elle permet le déplacement de l'eau et/ou de l'humidité à travers le sol, mais d'autre part, elle affecte les propriétés mécaniques du sol.
Il est donc essentiel de disposer d'indicateurs qui décrivent la présence de la porosité et la proportion d'eau qu'ils contiennent, car ces indicateurs jouent un rôle essentiel dans la caractérisation des propriétés hydrauliques, thermodynamiques et mécaniques du sol.
ID:(365, 0)
Modèle de volume solide, eau et gaz
Concept
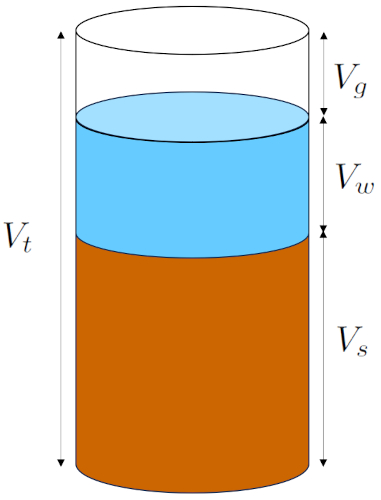
Dans le modèle de sol, le volume total ($V_t$) de l'échantillon se compose de trois composants principaux :
• le volume solide ($V_s$) : Cette composante comprend le volume de tous les grains présents dans l'échantillon.
• le volume d'eau ($V_w$) : Représente le volume d'eau contenu à la fois dans les micropores et les macropores du sol.
• le volume de gaz ($V_g$) : Comprend le volume de gaz ou d'air contenu dans l'échantillon.
Le schéma suivant résume cette description :
ID:(1642, 0)
Représentation de la profondeur effective
Image
A profondeur effective ($D_e$) fait référence à la profondeur à laquelle l'eau contenue dans un volume de sol atteindrait si tout le volume solide était "retiré", comme illustré dans l'image suivante :
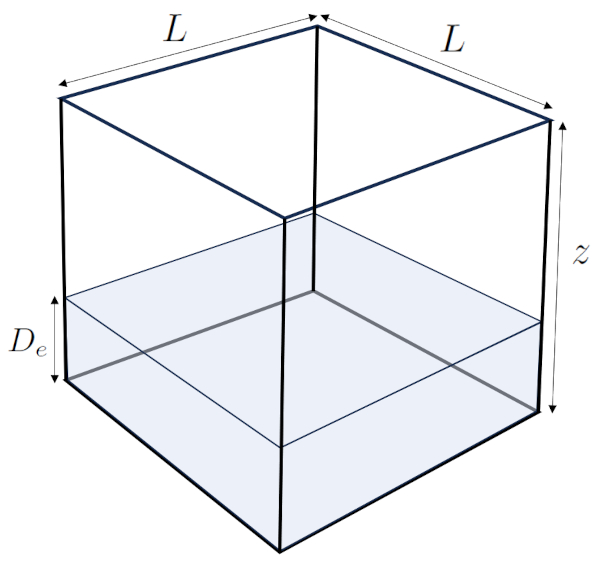
Cela fournit une mesure intuitive de la teneur en eau dans le sol.
ID:(1641, 0)
Modèle de masse solide, d'eau et de gaz
Concept
Dans le modèle du sol, a masse totale ($M_t$) de l'échantillon se compose de trois composants principaux :
• a masse sèche totale de l'échantillon ($M_s$) : Ce composant comprend les masses de tous les grains présents dans l'échantillon.
• a masse d'eau dans le sol ($M_w$) : Représente la masse de l'eau contenue à la fois dans les micropores et les macropores du sol.
• a masse de gaz dans le sol ($M_g$) : Comprend la masse du gaz ou de l'air contenu dans l'échantillon (qui peut être considérée de manière comparative comme presque nulle, c'est-à-dire $M_g\sim 0$).
ID:(2084, 0)
Surface interne
Concept
L'une des propriétés distinctives des particules, telles que le sol, est leur surface interne. Par surface interne, nous entendons la somme de toutes les surfaces de chacun des grains. Cette surface est l'un des facteurs clés pour étudier le comportement de l'humidité et la présence de nutriments dans le sol.
En multipliant la surface de chaque grain par sa quantité, nous obtenons la surface totale. Pour déterminer la surface de chaque grain, il est essentiel de prendre en compte sa forme. Il est important de rappeler que tant le sable que le limon sont modélisés comme des sphères, tandis que l'argile est représentée comme un parallélépipède droit.
ID:(1540, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ D_e = \theta_V z $
D_e = theta_V * z
$ e =\displaystyle\frac{ V_g + V_w }{ V_s }$
e =( V_g + V_w )/ V_s
$ f_g =\displaystyle\frac{ V_g }{ V_t }$
f_g = V_g / V_t
$ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$
g_M = S_t / M_s
$ M_t = M_s + M_w $
M_t = M_s + M_w
$ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$
Phi = 1 - rho_b / rho_p
$ \rho_b =\displaystyle\frac{ M_s }{ V_t }$
rho_b = M_s / V_t
$ \rho_w =\displaystyle\frac{ M_w }{ V_w }$
rho_w = M_w / V_w
$ S = \displaystyle\frac{ \theta_V }{ \Phi }$
S = theta_V / Phi
$ S_a = N_a s_a $
S_a = N_a * s_a
$ s_c = 2 l_c ^2 + 4 w_c l_c $
s_c = 2* l_c ^2 + 4* w_c * l_c
$ S_c = N_c s_c $
S_c = N_c * s_c
$ s_i = 6 a_i ^2 $
s_i = 6* a_i ^2
$ S_i = N_i s_i $
S_i = N_i * s_i
$ S_t = S_a + S_l + S_c $
S_t = S_a + S_l + S_c
$ \theta_r =\displaystyle\frac{ V_w }{ V_s }$
theta_r = V_w / V_s
$ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$
theta_s = V_w /( V_g + V_w )
$ \theta_V =\displaystyle\frac{ V_w }{ V_t }$
theta_V = V_w / V_t
$ \theta_w =\displaystyle\frac{ M_w }{ M_s }$
theta_w = M_w / M_s
$ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$
V_g = S_t / V_t
$ V_p = V_w + V_g $
V_p = V_w + V_g
$ V_t = V_s + V_w + V_g $
V_t = V_s + V_w + V_g
$ s_a = 4 \pi r_a ^2 $
s_k = 4* pi * r_a ^2
ID:(15219, 0)
Volume total avec eau
Équation
Le volume total ($V_t$) est obtenu en additionnant la partie solide des grains, qui correspond au le volume solide ($V_s$), à l'eau contenue dans le volume d'eau ($V_w$), et à l'air ou, en général, au gaz contenu dans le volume de gaz ($V_g$) :
| $ V_t = V_s + V_w + V_g $ |
ID:(15089, 0)
Volume poreux
Équation
Le volume poreux ($V_p$) n'est pas nécessairement vide ; il peut contenir de l'eau en particulier, c'est pourquoi nous introduisons la variable le volume d'eau ($V_w$). D'autre part, le volume restant est considéré comme le volume de gaz ($V_g$).
De cette manière, le le volume poreux ($V_p$) est calculé comme la somme des deux types de volumes :
| $ V_p = V_w + V_g $ |
ID:(4723, 0)
Rapport volumétrique de l'eau du sol
Équation
Un indicateur qui indique la proportion d'eau dans le volume total de l'échantillon est le a rapport volumétrique de l'eau du sol ($\theta_V$). Il est calculé en estimant le rapport entre le volume d'eau ($V_w$) et le volume total ($V_t$) :
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
ID:(4721, 0)
Rapport volumétrique d'eau solide
Équation
Un indicateur qui signifie la proportion d'eau dans le volume solide de l'échantillon est a propriété de porosité de l'argile ($\theta_r$). Il est calculé en estimant le rapport entre le volume d'eau ($V_w$) et le volume solide ($V_s$):
| $ \theta_r =\displaystyle\frac{ V_w }{ V_s }$ |
ID:(4722, 0)
Rapport de vide
Équation
La relation entre le volume d'eau et le volume solide compare la quantité d'eau à la quantité de solides dans le sol. Cependant, étant donné que le volume d'eau peut varier, il est intéressant de comparer le volume poreux ($V_p$), ou alternativement la somme de le volume de gaz ($V_g$) et le volume d'eau ($V_w$), avec le volume solide ($V_s$) pour définir l'indicateur a rapport de vide ($e$) comme suit:
| $ e =\displaystyle\frac{ V_g + V_w }{ V_s }$ |
ID:(4728, 0)
Porosité à l'air
Équation
A porosité ($f$) est définie comme la relation entre le volume poreux ($V_p$) et le volume total ($V_t$). De manière similaire, a porosité à l'air ($f_g$) est définie en fonction du volume non occupé par l'eau, c'est-à-dire le rapport entre le volume de gaz ($V_g$) et le volume total ($V_t$) :
| $ f_g =\displaystyle\frac{ V_g }{ V_t }$ |
ID:(4724, 0)
Saturation relative
Équation
A saturation relative ($\theta_s$) est calculée comme la proportion de la porosité occupée par l'eau, définie par le volume d'eau ($V_w$), divisée par la somme de le volume d'eau ($V_w$) et le volume de gaz ($V_g$), exprimée par :
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
ID:(4727, 0)
Profondeur effective
Équation
A rapport volumétrique de l'eau du sol ($\theta_V$) nous permet d'estimer la profondeur que l'eau atteindrait si le sol était retiré à une profondeur de a profondeur ($z$), ce qui est calculé à l'aide de l'équation suivante :
| $ D_e = \theta_V z $ |
Si vous disposez d'un volume de sol avec une largeur et une longueur $L$ et a profondeur ($z$), son volume est représenté par l'équation suivante :
$V_t = L^2z$
Avec a profondeur effective ($D_e$) représentant une variable importante, le volume d'eau peut être calculé comme suit :
$V_w = L^2D_e$
De plus, avec l'équation
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
nous pouvons relier ces variables comme suit :
$\theta_V = \displaystyle\frac{V_w}{V_t} = \displaystyle\frac{D_e}{z}$
Par conséquent, la variable a profondeur effective ($D_e$) peut être calculée à l'aide de l'expression suivante :
| $ D_e = \theta_V z $ |
ID:(3231, 0)
Masse totale
Équation
A masse totale ($M_t$) est calculée en ajoutant a masse sèche totale de l'échantillon ($M_s$) et a masse d'eau dans le sol ($M_w$) ensemble, comme suit :
| $ M_t = M_s + M_w $ |
ID:(4247, 0)
Densité apparente
Équation
En général, la densité est définie comme le rapport de la masse au volume d'un matériau. Dans le cas du sol, qui contient de la porosité, lors de l'utilisation de le volume total ($V_t$), on inclut le volume solide ($V_s$), le volume d'eau ($V_w$), et le volume poreux ($V_p$). Généralement, la densité apparente est calculée pour le matériau sec, c'est-à-dire sans eau ($M_w \sim 0$), de sorte que a masse totale ($M_t$) soit égale à A masse sèche totale de l'échantillon ($M_s$) :
$M_t\sim M_s$
Il est important de noter que ceci est une approximation, car lors du séchage du sol, une petite quantité d'eau reste toujours, ce qui rend très difficile la mesure précise de la masse solide sans eau.
Par conséquent, nous définissons a densité apparente sèche ($\rho_b$) comme le rapport de a masse d'eau dans le sol ($M_w$) à Le volume total ($V_t$) :
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
ID:(4719, 0)
Densité de l'eau
Équation
Lorsque l'on travaille avec de l'eau, il est également essentiel de prendre en compte la variable a densité de l'eau ($\rho_w$), qui est calculée à partir de a masse d'eau dans le sol ($M_w$) et le volume d'eau ($V_w$) en utilisant l'équation suivante :
| $ \rho_w =\displaystyle\frac{ M_w }{ V_w }$ |
ID:(4730, 0)
Rapport gravimétrique eau-solide
Équation
Si nous souhaitons indiquer dans quelle mesure le sol contient de l'eau, nous pouvons introduire un indicateur appelé A propriété de porosité de l'argile ($\theta_w$), qui est calculé comme le rapport de a masse d'eau dans le sol ($M_w$) à A masse sèche totale de l'échantillon ($M_s$), en utilisant la formule suivante :
| $ \theta_w =\displaystyle\frac{ M_w }{ M_s }$ |
ID:(4720, 0)
Surface d'un grain de sable
Équation
Puisque nous modélisons un grain de sable comme une sphère, son a surface d'un grain de sable ($s_a$) peut être calculé en fonction du le rayon du grain de sable ($r_a$) de la manière suivante :
| $ s_a = 4 \pi r_a ^2 $ |
ID:(3167, 0)
Surface d'un grain de limon
Équation
Puisque nous modélisons un grain de limon comme un cube, son a surface d'un grain de limon ($s_i$) peut être calculé en fonction du le côté grain de limon ($a_i$) de la manière suivante :
| $ s_i = 6 a_i ^2 $ |
ID:(3169, 0)
Surface d'un grain d'argile
Équation
Puisque nous modélisons un grain d'argile comme un parallélépipède rectangle, son a surface d'un grain d'argile ($s_c$) peut être calculé en fonction du le longueur et largeur d'une plaque d'argile ($l_c$) et du a hauteur d'une plaque d'argile ($w_c$) du grain d'argile comme suit :
| $ s_c = 2 l_c ^2 + 4 w_c l_c $ |
ID:(4361, 0)
Surface des grains de sable
Équation
A surface des grains de sable ($S_a$) peut être calculée à partir le nombre de grains de sable dans l'échantillon ($N_a$) et a surface d'un grain de sable ($s_a$) comme suit :
| $ S_a = N_a s_a $ |
ID:(929, 0)
Surface des grains de limon
Équation
A surface des grains de limon ($S_i$) peut être calculée à partir le nombre de grains de limon dans l'échantillon ($N_i$) et a surface d'un grain de limon ($s_i$) comme suit :
| $ S_i = N_i s_i $ |
ID:(33, 0)
Surface des grains d'argile
Équation
A superfície de grão de argila ($S_c$), qui peut être calculée à partir le nombre de grains d'argile dans l'échantillon ($N_c$) et a surface d'un grain de limon ($s_i$) comme suit :
| $ S_c = N_c s_c $ |
ID:(35, 0)
Surface interne du sol
Équation
Étant donné que les grains n'ont que de plus petites sections en contact, nous pouvons supposer, dans une première approximation, que leur surface entière est disponible pour absorber l'eau et soutenir la vie. Par conséquent, nous introduisons le concept de "surface intérieure du sol" et la décrivons comme la somme de toutes les surfaces des grains. De cette manière, si la a surface interne du sol ($S_t$) est obtenue comme la somme de a surface des grains de sable ($S_a$), a surface des grains de limon ($S_i$), et
| $ S_t = S_a + S_l + S_c $ |
ID:(3166, 0)
Surface interne par masse
Équation
Le problème avec a surface interne du sol ($S_t$) est qu'il dépend de la taille de l'échantillon et ne fournit donc pas un indicateur de la capacité de surface du sol.
Une alternative consiste à normaliser la valeur de la surface interne avec a masse totale ($M_t$), ce qui donne l'indicateur a surface d'un grain de limon ($\gamma_M$) :
| $ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$ |
ID:(4718, 0)
Surface interne en volume
Équation
Le problème avec a surface interne du sol ($S_t$) est qu'il dépend de la taille de l'échantillon et ne fournit donc pas un indicateur de la capacité de surface du sol.
Une alternative consiste à normaliser la valeur de a surface interne du sol ($S_t$) en utilisant le volume total ($V_t$), ce qui donne l'indicateur a surface interne en volume ($\gamma_V$) :
| $ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$ |
ID:(4717, 0)
Porosité de masse
Équation
A porosité de masse ($\Phi$) est initialement défini de la même manière que a porosité ($f$), cependant, il est estimé en fonction de a densité apparente sèche ($\rho_b$) et a densité de particules ($\rho_p$) de la manière suivante :
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
La définition de a porosité ($f$) est effectuée avec le volume solide ($V_s$) et le volume total ($V_t$), qui peuvent être modifiés avec a masse sèche totale de l'échantillon ($M_s$) et la définition :
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
ce qui donne :
$\Phi=1-\displaystyle\frac{V_s}{V_t}=1-\displaystyle\frac{V_s}{M_s}\displaystyle\frac{M_s}{V_t}=\displaystyle\frac{V_s}{M_s}\rho_b$
Bien que la relation entre a masse sèche totale de l'échantillon ($M_s$) et le volume solide ($V_s$) corresponde à A densité solide ($\rho_s$), cette densité peut être estimée en utilisant a densité de particules ($\rho_p$), ce qui conduit à
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
ID:(15128, 0)
Degré de saturation massique
Équation
Le saturation massique relative ($\theta_S$) est initialement défini de la même manière que a saturation relative ($\theta_s$), en utilisant les volumes. Cependant, au lieu d'utiliser a porosité ($f$), vous pouvez utiliser a porosité de masse ($\Phi$) à la place, ce qui donne un degré de saturation basé sur la masse :
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
A saturation relative ($\theta_s$) est calculé en utilisant le volume d'eau ($V_w$) et le volume de gaz ($V_g$) comme suit :
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
Comme avec a porosité ($f$) et le volume total ($V_t$),
$V_w + V_g = f V_t$
et puisque a rapport volumétrique de l'eau du sol ($\theta_V$) est
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
alors
$\theta_s=\displaystyle\frac{V_w}{V_w+V_g}=\displaystyle\frac{V_w}{fV_t}=\displaystyle\frac{\theta_V}{f}$
Si a porosité ($f$) est estimé en utilisant le volume et remplacé par celui estimé avec la masse a porosité de masse ($\Phi$), nous obtenons
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
ID:(15129, 0)