Storyboard

La microporosité du sol dépend de sa composition, il est donc important de pouvoir la modéliser en fonction de la proportion des différentes composantes. Pour ce faire, on étudie d'abord le facteur volumétrique des différentes textures, puis on estime la porosité en tenant compte du fait qu'il existe une composante de base fournie par l'argile. De plus, la présence de sable et de limon est prise en compte, mais il est important de noter que l'argile peut pénétrer dans les espaces entre les grains, ce qui réduit la porosité totale.

>Modèle

ID:(2050, 0)

Iframe

>Top

ID:(15199, 0)

Concept

>Top

Dans le cas des sols en général, nous pouvons étudier le triangle de texture du sol. Si nous décrivons la plage typique de porosité observée pour chaque type de sol, nous pouvons voir ce qui a été discuté précédemment. Dans le coin où le sable prédomine, nous avons une porosité qui peut atteindre jusqu'à 25 %, ce qui est optimal pour un modèle de sphères :

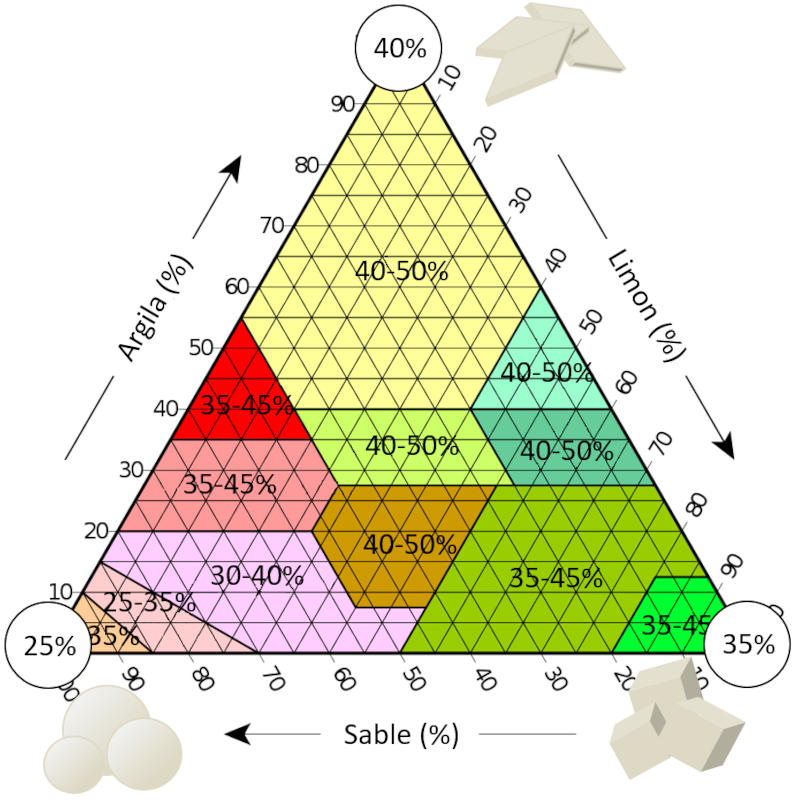
Triangle de texture qui inclut la plage de porosité obtenue à partir de [1] et [2].

Maintenant, si nous examinons le coin du limon, nous pouvons voir qu'une porosité de 35 % peut être atteinte, ce qui correspond au niveau d'espace qui ne peut pas être rempli par des cubes. Cela signifie que le matériau n'est pas capable de s'organiser de manière à exploiter la structure cubique. Cela est probablement une conséquence des forces attractives à l'échelle des microns qui entraînent un empilement désordonné.

Dans le dernier cas, nous pouvons voir la limite de l'argile, où la porosité atteint une valeur d'environ 40 %, ce qui doit à nouveau être une conséquence de l'interaction entre les plaques qui peuvent organiser des groupes d'entre elles, mais pas l'ensemble du système.

En résumé, nous observons qu'au coin inférieur gauche, où le sol est principalement composé de sable, la porosité peut atteindre 25 %. Ces 25 % représentent précisément la porosité atteinte dans le meilleur des cas pour un modèle de sphères.

En d'autres termes, il existe une porosité inhérente spécifique aux types de sol, et dans les sols avec une présence significative d'argile, l'argile domine. L'effet du sable et du limon ne prédomine que dans les cas extrêmes où le matériau contient très peu d'argile.

[1] Soil Mechanics and Foundations, Muni Budhu, (2011), John Wiley & Sons.

[2] Principles of Geotechnical Engineering, Braja M. Das, (2010), Cengage Learning

ID:(2078, 0)

Concept

>Top

Si l'on suppose que les densités des différentes composantes sont similaires :

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

les facteurs de volume a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$) en fonction de a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$), et a fraction massique d'argile dans l'échantillon ($g_c$) peuvent être exprimés comme suit :

$f_a = (1-f)\displaystyle\frac{\rho_s}{\rho_a}g_a \sim (1-f)g_a$

$f_i = (1-f)\displaystyle\frac{\rho_s}{\rho_i}g_i \sim (1-f)g_i$

$f_c = (1-f)\displaystyle\frac{\rho_s}{\rho_c}g_c \sim (1-f)g_c$

Cela nous permet d'estimer la plage de facteurs volumétriques pour différents types de sols, y compris lorsque a porosité ($f$) et a fraction volumique des macropores dans l'échantillon ($f_m$) sont nuls :

ID:(15096, 0)

Description

>Top

Étant donné les informations que nous avons pour le calcul de l'équation de porosité ($p_p$), le propre facteur de volume du sable ($p_a$), le facteur de volume propre au slime ($p_i$), le facteur de volume propre à l'argile ($p_c$), a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$), qui satisfont l'équation :

et que nous connaissons les valeurs moyennes pour différentes textures de sol avec leurs a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$), a fraction massique d'argile dans l'échantillon ($g_c$) et le calcul de l'équation de porosité ($p_p$) respectifs comme suit :

Nous pouvons effectuer une régression pour déterminer les valeurs de a température en degrés Celsius à l'état 2 ($t_2$), le propre facteur de volume du sable ($p_a$) et le facteur de volume propre au slime ($p_i$). Le résultat est un ajustement avec un R carré de 0,974 et les paramètres sont les suivants :

En général, le niveau de compactage du sable avec un a porosité du sable ($q_a$) d'environ 25 % correspond à un compactage maximal. Cependant, avec un a porosité du limon ($q_i$) d'environ 47 %, il est supérieur à l'optimum, tout comme les 49 % pour a porosité de l'argile ($q_c$). Dans tous les cas, les facteurs sont une bonne estimation compte tenu du R carré élevé et des faibles valeurs de p-test pour chaque facteur, qui sont significativement inférieures au seuil traditionnel de 0,05. Les tentatives de prendre en compte d'autres puissances dans la régression montrent que l'approximation linéaire est la seule qui produit des coefficients inférieurs à 0,05, ce qui suggère que les échantillons doivent avoir des distributions qui ne présentent pas d'importants effets de mélange et sont simplement des sommes de composants, tels que des agrégats.

ID:(15099, 0)

Top

>Top

Paramètres

$\rho_i$

rho_i

Densité d'un grain de limon

kg/m^3

$\rho_a$

rho_a

Densité d'un grain de sable

kg/m^3

$\rho_s$

rho_s

Densité solide

kg/m^3

$\rho_c$

rho_c

Longueur et largeur d'une plaque d'argile

kg/m^3

Variables

$p_p$

p_p

Calcul de l'équation de porosité

-

$p_c$

p_c

Facteur de volume propre à l'argile

-

$p_i$

p_i

Facteur de volume propre au slime

-

$f_c$

f_c

Force par grain

N

$g_c$

g_c

Fraction massique d'argile dans l'échantillon

-

$g_i$

g_i

Fraction massique de limon dans l'échantillon

-

$g_a$

g_a

Fraction massique de sable dans l'échantillon

-

$f_c$

f_c

Fraction volumique d'argile dans l'échantillon

-

$f_i$

f_i

Fraction volumique de limon dans l'échantillon

-

$f_a$

f_a

Fraction volumique de sable dans l'échantillon

-

$f_m$

f_m

Fraction volumique des macropores dans l'échantillon

-

$f$

f

Porosité

-

$q_c$

q_c

Porosité de l'argile

-

$q_i$

q_i

Porosité du limon

-

$q_a$

q_a

Porosité du sable

-

$p_a$

p_a

Propre facteur de volume du sable

-

$V_m$

V_m

Volume des macropores

m^3

$V_c$

V_c

Volume solide d'argile

m^3

$V_i$

V_i

Volume solide de limon

m^3

$V_a$

V_a

Volume solide de sable

m^3

$V_t$

V_t

Volume total

m^3

Calculs

• Méthode alternative
• Méthode traditionnelle
• Stratégie
• 2D
• 3D

Équation

Nombre

D'abord, sélectionnez l'équation: à , puis, sélectionnez la variable: à

---

Calculs

Symbole

Équation

Résolu

Traduit

Calculs

Symbole

Équation

Résolu

Traduit

Variable Donnée Calculer Cible : Équation À utiliser

Équations

ID:(15218, 0)

Équation

>Top, >Modèle

De manière similaire à la façon dont les proportions entre les masses de chaque composant et la masse totale sont définies, nous pouvons établir un système analogue en utilisant les volumes. Avec cela à l'esprit, nous pouvons définir a fraction volumique de sable dans l'échantillon ($f_a$) par rapport à Le volume total ($V_t$). Cela nous permettra de calculer la quantité de le volume solide de sable ($V_a$) dans le contexte de le volume total ($V_t$).

$f_a = \displaystyle\frac{ V_a }{ V_t }$

Conditions

Variables

$f_a$

Fraction volumique de sable dans l'échantillon

$-$

10105

$V_a$

Volume solide de sable

$m^3$

6554

$V_t$

Volume total

$m^3$

4946

Relation

ID:(10369, 0)

Équation

>Top, >Modèle

De manière similaire à la façon dont les proportions entre les masses de chaque composant et la masse totale sont définies, nous pouvons établir un système analogue en utilisant les volumes. Avec cela à l'esprit, nous pouvons définir a fraction volumique de limon dans l'échantillon ($f_i$) par rapport à Le volume total ($V_t$). Cela nous permettra de calculer la quantité de le volume solide de limon ($V_i$) dans le contexte de le volume total ($V_t$).

$f_i = \displaystyle\frac{ V_i }{ V_t }$

Conditions

Variables

$f_i$

Fraction volumique de limon dans l'échantillon

$-$

10106

$V_i$

Volume solide de limon

$m^3$

6555

$V_t$

Volume total

$m^3$

4946

Relation

ID:(10367, 0)

Équation

>Top, >Modèle

De manière similaire à la façon dont les proportions entre les masses de chaque composant et la masse totale sont définies, nous pouvons établir un système analogue en utilisant les volumes. Avec cela à l'esprit, nous pouvons définir a fraction volumique d'argile dans l'échantillon ($f_c$) par rapport à Le volume total ($V_t$). Cela nous permettra de calculer la quantité de le volume total ($V_t$) dans le contexte du volume total.

$f_c = \displaystyle\frac{ V_c }{ V_t }$

Conditions

Variables

$f_c$

Force par grain

$N$

8270

$V_c$

Volume solide d'argile

$m^3$

6556

$V_t$

Volume total

$m^3$

4946

Relation

ID:(10368, 0)

Équation

>Top, >Modèle

De manière similaire à la façon dont les proportions entre les masses de chaque composant et la masse totale sont définies, nous pouvons établir un système analogue en utilisant les volumes. Avec cela à l'esprit, nous pouvons définir a fraction volumique des macropores dans l'échantillon ($f_m$) par rapport à Le volume total ($V_t$). Cela nous permettra de calculer la quantité de le volume des macropores ($V_m$) dans le contexte de le volume total ($V_t$).

$f_m = \displaystyle\frac{ V_m }{ V_t }$

Conditions

Variables

$f_m$

Fraction volumique des macropores dans l'échantillon

$-$

10110

$V_m$

Volume des macropores

$m^3$

10109

$V_t$

Volume total

$m^3$

4946

Relation

ID:(15084, 0)

Équation

>Top, >Modèle

La condition pour les sols argileux en fonction de le volume solide de sable ($V_a$), le volume solide de limon ($V_i$), le volume solide d'argile ($V_c$), le volume des macropores ($V_m$), le propre volume ($V_z$) et a porosité de l'argile ($q_c$) est exprimée comme suit :

Lorsque nous utilisons l'équation pour le volume total ($V_t$) en fonction de le propre volume ($V_z$) et la divisons par le volume total ($V_t$), nous pouvons la réécrire en fonction de a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$) et a fraction volumique des macropores dans l'échantillon ($f_m$) comme suit :

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

Conditions

Variables

$f_c$

Fraction volumique d'argile dans l'échantillon

$-$

10107

$f_i$

Fraction volumique de limon dans l'échantillon

$-$

10106

$f_a$

Fraction volumique de sable dans l'échantillon

$-$

10105

$f_m$

Fraction volumique des macropores dans l'échantillon

$-$

10110

$q_c$

Porosité de l'argile

$-$

10104

$q_i$

Porosité du limon

$-$

10103

$q_a$

Porosité du sable

$-$

10102

Relation

Développement

Avec l'équation du le volume total ($V_t$) en fonction du le propre volume ($V_z$) et des le volume des macropores ($V_m$) :

$V_t = V_m + V_z$

en remplaçant le le propre volume ($V_z$) en fonction du le volume solide de sable ($V_a$), du le volume solide de limon ($V_i$), du le volume solide d'argile ($V_c$), du le volume des macropores ($V_m$) et du a porosité de l'argile ($q_c$) par :

$V_z = V_a + V_i + \displaystyle\frac{1}{1- q_c } V_c$

nous obtenons :

$V_t = V_a + V_i + \displaystyle\frac{1}{1-q_c}V_c+V_m$

Si nous divisons cette équation par le volume total ($V_t$) et utilisons les définitions de a fraction volumique de sable dans l'échantillon ($f_a$)

$f_a = \displaystyle\frac{ V_a }{ V_t }$

pour le a fraction volumique de limon dans l'échantillon ($f_i$)

$f_i = \displaystyle\frac{ V_i }{ V_t }$

pour le a fraction volumique d'argile dans l'échantillon ($f_c$)

$f_c = \displaystyle\frac{ V_c }{ V_t }$

et pour les a fraction volumique des macropores dans l'échantillon ($f_m$)

$f_m = \displaystyle\frac{ V_m }{ V_t }$

nous obtenons la relation suivante :

$\displaystyle\frac{1}{1- q_a } f_a + \displaystyle\frac{1}{1- q_i } f_i + \displaystyle\frac{1}{1- q_c } f_c + f_m = 1$

ID:(15086, 0)

Équation

>Top, >Modèle

Le volume poreux ($V_p$) dans un matériau argileux, qui est une fonction du volume des le volume des macropores ($V_m$), a porosité de l'argile ($q_c$) et le volume solide d'argile ($V_c$) :

peut être réécrite en divisant l'équation par le volume total ($V_t$) et en exprimant l'équation en termes de a porosité ($f$), a fraction volumique des macropores dans l'échantillon ($f_m$) et a fraction volumique d'argile dans l'échantillon ($f_c$), ce qui donne :

$f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c$

Conditions

Variables

$f_c$

Fraction volumique d'argile dans l'échantillon

$-$

10107

$f_i$

Fraction volumique de limon dans l'échantillon

$-$

10106

$f_a$

Fraction volumique de sable dans l'échantillon

$-$

10105

$f$

Porosité

$-$

5805

$q_c$

Porosité de l'argile

$-$

10104

$q_i$

Porosité du limon

$-$

10103

$q_a$

Porosité du sable

$-$

10102

Relation

Développement

Le calcul de le volume poreux ($V_p$) peut être effectué en utilisant les volumes de le volume des macropores ($V_m$), le volume solide d'argile ($V_c$) et a porosité de l'argile ($q_c$) avec l'équation suivante :

$V_p = V_m + \displaystyle\frac{ q_a }{1- q_a } V_a + \displaystyle\frac{ q_i }{1- q_i } V_i + \displaystyle\frac{ q_c }{1- q_c } V_c$

En divisant cette équation par le volume total ($V_t$), nous pouvons utiliser a porosité ($f$)

$f =\displaystyle\frac{ V_p }{ V_t }$

ainsi que a fraction volumique des macropores dans l'échantillon ($f_m$)

$f_m = \displaystyle\frac{ V_m }{ V_t }$

et a fraction volumique d'argile dans l'échantillon ($f_c$)

$f_c = \displaystyle\frac{ V_c }{ V_t }$

ce qui se simplifie en

$f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c$

.

ID:(2074, 0)

Équation

>Top, >Modèle

Comment a fraction volumique de sable dans l'échantillon ($f_a$) a été défini en fonction de le volume solide de sable ($V_a$) et le volume total ($V_t$) :

Par conséquent, avec a densité d'un grain de sable ($\rho_a$), a densité solide ($\rho_s$), a porosité ($f$) et a fraction massique de sable dans l'échantillon ($g_a$) vous pouvez calculer le facteur à l'aide de :

$f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a$

Conditions

Variables

$\rho_a$

Densité d'un grain de sable

2.63e+3

$kg/m^3$

10095

$\rho_s$

Densité solide

$kg/m^3$

4944

$g_a$

Fraction massique de sable dans l'échantillon

$-$

5797

$f_a$

Fraction volumique de sable dans l'échantillon

$-$

10105

$f$

Porosité

$-$

5805

Relation

Développement

Pour calculer a fraction volumique de sable dans l'échantillon ($f_a$), vous pouvez utiliser la définition avec le volume solide de sable ($V_a$) et le volume total ($V_t$) comme suit :

$f_a = \displaystyle\frac{ V_a }{ V_t }$

le volume solide de sable ($V_a$) peut être exprimé avec a densité d'un grain de sable ($\rho_a$) et a masse sèche de sable dans l'échantillon ($M_a$) en utilisant l'équation :

$V_a =\displaystyle\frac{ M_a }{ \rho_a }$

Pour le volume total ($V_t$), vous pouvez travailler avec le volume solide ($V_s$) et le volume poreux ($V_p$) en utilisant l'équation :

$V_t = V_s + V_p$

en utilisant l'expression pour a porosité ($f$) :

$f =\displaystyle\frac{ V_p }{ V_t }$

Avec ces deux équations, vous obtenez l'expression :

$V_t = \displaystyle\frac{1}{1-f} V_s$

En utilisant la définition de a densité solide ($\rho_s$) avec a masse sèche totale de l'échantillon ($M_s$) et le volume solide ($V_s$) :

$\rho_s = \displaystyle\frac{ M_s }{ V_s }$

vous pouvez exprimer le volume total ($V_t$) comme suit :

$V_t = \displaystyle\frac{M_s}{(1-f)\rho_s}$

De cette manière, vous obtenez l'expression de a fraction volumique de sable dans l'échantillon ($f_a$) comme suit :

$f_a= \displaystyle\frac{V_a}{V_t}= \displaystyle\frac{M_a}{M_s} \displaystyle\frac{(1-f)\rho_s}{\rho_a}$

ce qui, avec l'équation pour a fraction massique de sable dans l'échantillon ($g_a$) :

$g_a =\displaystyle\frac{ M_a }{ M_s }$

se réduit à :

$f_a = (1- f )\displaystyle\frac{ \rho_s }{ \rho_a } g_a$

ID:(15093, 0)

Équation

>Top, >Modèle

Comment a fraction volumique de sable dans l'échantillon ($f_a$) a été défini en fonction de le volume solide de limon ($V_i$) et le volume total ($V_t$) :

Par conséquent, avec a densité d'un grain de limon ($\rho_i$), a densité solide ($\rho_s$), a porosité ($f$) et a fraction massique de limon dans l'échantillon ($g_i$) vous pouvez calculer le facteur en utilisant :

$f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i$

Conditions

Variables

$\rho_i$

Densité d'un grain de limon

2.65e+3

$kg/m^3$

10094

$\rho_s$

Densité solide

$kg/m^3$

4944

$g_i$

Fraction massique de limon dans l'échantillon

$-$

10098

$f_i$

Fraction volumique de limon dans l'échantillon

$-$

10106

$f$

Porosité

$-$

5805

Relation

ID:(15094, 0)

Équation

>Top, >Modèle

Comment a fraction volumique de sable dans l'échantillon ($f_a$) a été défini en fonction de le volume solide d'argile ($V_c$) et le volume total ($V_t$) :

Par conséquent, avec a longueur et largeur d'une plaque d'argile ($\rho_c$), a densité solide ($\rho_s$), a porosité ($f$) et a fraction massique d'argile dans l'échantillon ($g_c$), vous pouvez calculer le facteur en utilisant :

$f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c$

Conditions

Variables

$\rho_s$

Densité solide

$kg/m^3$

4944

$g_c$

Fraction massique d'argile dans l'échantillon

$-$

10099

$f_c$

Fraction volumique d'argile dans l'échantillon

$-$

10107

$\rho_c$

Longueur et largeur d'une plaque d'argile

2.8e+3

$kg/m^3$

10093

$f$

Porosité

$-$

5805

Relation

ID:(15095, 0)

Équation

>Top, >Modèle

A porosité ($f$) est une fonction de a fraction volumique des macropores dans l'échantillon ($f_m$), a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$), a porosité du sable ($q_a$), a porosité du limon ($q_i$) et a porosité de l'argile ($q_c$) :

En utilisant les relations entre les facteurs volumétriques et les facteurs de masse a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$), en supposant l'absence de macropores et des densités égales pour les trois composantes, nous obtenons :

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Conditions

Variables

$g_c$

Fraction massique d'argile dans l'échantillon

$-$

10099

$g_i$

Fraction massique de limon dans l'échantillon

$-$

10098

$g_a$

Fraction massique de sable dans l'échantillon

$-$

5797

$f$

Porosité

$-$

5805

$q_c$

Porosité de l'argile

$-$

10104

$q_i$

Porosité du limon

$-$

10103

$q_a$

Porosité du sable

$-$

10102

Relation

Développement

A porosité ($f$) est une fonction de le nombre de grains de limon dans l'échantillon ($N_i$), a fraction volumique de sable dans l'échantillon ($f_a$), a fraction volumique de limon dans l'échantillon ($f_i$), a fraction volumique d'argile dans l'échantillon ($f_c$), a porosité du sable ($q_a$), a porosité du limon ($q_i$) et a porosité de l'argile ($q_c$) :

$f = f_m + \displaystyle\frac{ q_a }{1- q_a } f_a + \displaystyle\frac{ q_i }{1- q_i } f_i + \displaystyle\frac{ q_c }{1- q_c } f_c$

Étant donné que avec a densité solide ($\rho_s$), a densité d'un grain de sable ($\rho_a$) et a fraction massique de sable dans l'échantillon ($g_a$) nous avons :

$f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c$

et avec a densité d'un grain de limon ($\rho_i$) et a fraction massique de limon dans l'échantillon ($g_i$) nous avons :

$f_i = (1- f )\displaystyle\frac{ \rho_s }{ \rho_i } g_i$

De plus, avec a longueur et largeur d'une plaque d'argile ($\rho_c$) et a fraction massique d'argile dans l'échantillon ($g_c$) nous avons :

$f_c = (1- f )\displaystyle\frac{ \rho_s }{ \rho_c } g_c$

il est possible, dans le cas où les densités sont égales :

$\rho_s\sim\rho_a\sim\rho_i\sim\rho_c$

et qu'il n'y ait pas de macropores :

$f_m\sim 0$

d'obtenir la relation suivante :

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

ID:(10370, 0)

Équation

>Top, >Modèle

Avec a porosité du sable ($q_a$), on peut définir le propre facteur de volume du sable ($p_a$) comme suit :

$p_a = \displaystyle\frac{ q_a }{1- q_a }$

Conditions

Variables

$q_a$

Porosité du sable

$-$

10102

$p_a$

Propre facteur de volume du sable

$-$

6557

Relation

ID:(15087, 0)

Équation

>Top, >Modèle

Avec a porosité du limon ($q_i$), vous pouvez définir le facteur de volume propre au slime ($p_i$) comme suit :

$p_i = \displaystyle\frac{ q_i }{1- q_i }$

Conditions

Variables

$p_i$

Facteur de volume propre au slime

$-$

6558

$q_i$

Porosité du limon

$-$

10103

Relation

ID:(15088, 0)

Équation

>Top, >Modèle

Avec a porosité de l'argile ($q_c$), vous pouvez définir le facteur de volume propre à l'argile ($p_c$) comme suit :

$p_c = \displaystyle\frac{ q_c }{1- q_c }$

Conditions

Variables

$p_c$

Facteur de volume propre à l'argile

$-$

6559

$q_c$

Porosité de l'argile

$-$

10104

Relation

ID:(15098, 0)

Équation

>Top, >Modèle

Avec a porosité ($f$), vous pouvez définir le calcul de l'équation de porosité ($p_p$) comme suit :

$p_p = \displaystyle\frac{ f }{1- f }$

Conditions

Variables

$p_p$

Calcul de l'équation de porosité

$-$

6053

$f$

Porosité

$-$

5805

Relation

ID:(2076, 0)

Équation

>Top, >Modèle

En utilisant a porosité ($f$), a porosité du sable ($q_a$), a porosité du limon ($q_i$), a porosité de l'argile ($q_c$), a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$),

peut être réécrit avec les définitions de le calcul de l'équation de porosité ($p_p$), le propre facteur de volume du sable ($p_a$), le facteur de volume propre au slime ($p_i$) et le facteur de volume propre à l'argile ($p_c$) comme suit :

$p_p = p_a g_a + p_i g_i + p_c g_c$

Conditions

Variables

$p_p$

Calcul de l'équation de porosité

$-$

6053

$p_c$

Facteur de volume propre à l'argile

$-$

6559

$p_i$

Facteur de volume propre au slime

$-$

6558

$g_c$

Fraction massique d'argile dans l'échantillon

$-$

10099

$g_i$

Fraction massique de limon dans l'échantillon

$-$

10098

$g_a$

Fraction massique de sable dans l'échantillon

$-$

5797

$p_a$

Propre facteur de volume du sable

$-$

6557

Relation

Développement

Avec les variables a porosité ($f$), a porosité du sable ($q_a$), a porosité du limon ($q_i$), a porosité de l'argile ($q_c$), a fraction massique de sable dans l'échantillon ($g_a$), a fraction massique de limon dans l'échantillon ($g_i$) et a fraction massique d'argile dans l'échantillon ($g_c$), nous avons la relation suivante :

$\displaystyle\frac{ f }{1- f }= \displaystyle\frac{ q_a }{1- q_a } g_a +\displaystyle\frac{ q_i }{1- q_i } g_i + \displaystyle\frac{ q_c }{1- q_c } g_c$

Si nous considérons la relation pour le calcul de l'équation de porosité ($p_p$) comme suit :

$p_p = \displaystyle\frac{ f }{1- f }$

La relation pour le propre facteur de volume du sable ($p_a$) comme suit :

$p_a = \displaystyle\frac{ q_a }{1- q_a }$

La relation pour le facteur de volume propre au slime ($p_i$) comme suit :

$p_i = \displaystyle\frac{ q_i }{1- q_i }$

Et la relation pour le facteur de volume propre à l'argile ($p_c$) comme suit :

$p_c = \displaystyle\frac{ q_c }{1- q_c }$

Alors le résultat global est le suivant :

$p_p = p_a g_a + p_i g_i + p_c g_c$

ID:(1542, 0)