Usuario: 
Composición de Suelos
Storyboard 
Las principales componentes del suelo comprenden tanto la arena (tanto gruesa como fina), el limo y la arcilla. La proporción de estas tres componentes varía en función del tipo de suelo. Debido a las notables diferencias en el tamaño de partícula entre estas componentes, se generan espacios denominados poros. Estos poros tienen la capacidad de albergar o facilitar el flujo de agua, lo que, a su vez, incide en el nivel de humedad de la porción de suelo que no se encuentra completamente saturada.
ID:(363, 0)
Modelo de suelo
Imagen
Los suelos presentan una estructura básica compuesta por diversas capas, cuya formación se debe a procesos iniciales de desarrollo y a la influencia de factores como la erosión y la vegetación. Aunque el grosor de estas capas puede variar significativamente, su contenido de materia orgánica sigue patrones claros:
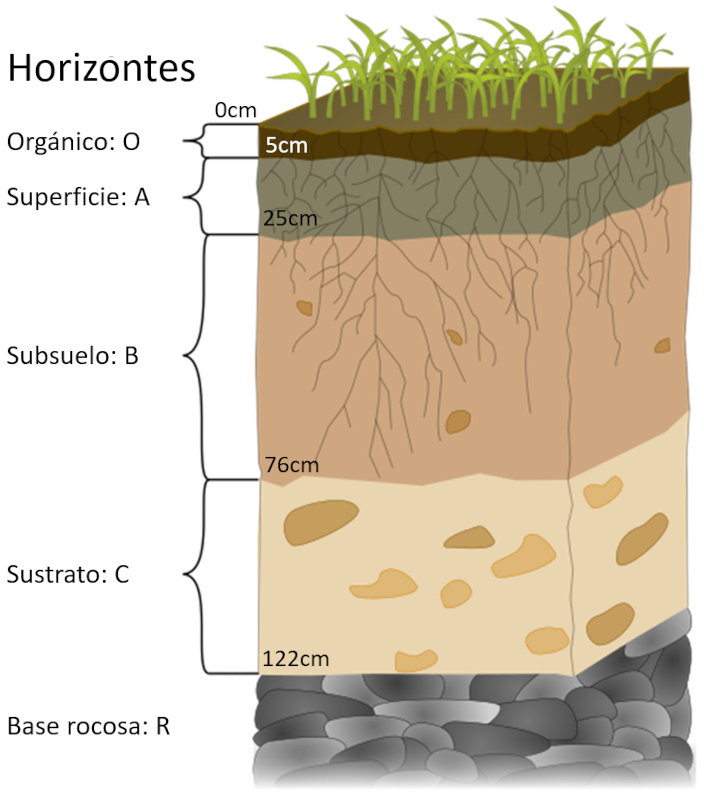
Perfil del suelo (commons.wikimedia.org - traducido)
O: Capa Orgánica de Superficie
Esta capa se origina debido a la acumulación de materia orgánica, compuesta principalmente por material vegetal en descomposición y humus. La cantidad de material orgánico puede alcanzar hasta el 100%, dependiendo de la vegetación y su desarrollo.
A: Suelo de Superficie
El horizonte A se forma por la erosión de minerales presentes, la adición de materia orgánica desde el horizonte superior y la actividad de organismos del suelo. La mayor parte de esta capa consiste en componentes minerales del suelo, con un contenido de materia orgánica que puede llegar al 10%.
B: Subsuelo
La capa B acumula minerales y materiales lixiviados que se desplazan desde el horizonte A. Esta acumulación también puede resultar de la llegada de minerales transportados desde otras áreas y de procesos químicos que ocurren en el horizonte. En esta capa, la mayoría de los componentes son minerales del suelo, y el contenido de materia orgánica puede llegar al 5%.
C: Sustrato
El horizonte C se forma principalmente debido a procesos geológicos y contribuye a la configuración general del terreno, proporcionando materiales que interactúan con las capas superiores. En esta capa, la mayor parte de los componentes son minerales del suelo, y el contenido de materia orgánica puede alcanzar el 1%.
El espesor de las dos primeras capas varía desde algunos centímetros hasta varias decenas de centímetros, mientras que las últimas pueden tener desde decenas de centímetros hasta metros de espesor. Es importante destacar que los valores de grosor mencionados en la imagen de Wikipedia son únicamente ejemplos ilustrativos y pueden variar ampliamente en la realidad.
ID:(15066, 0)
Uso de tamices para separar componentes
Concepto
El suelo está compuesto por arena, limo y arcilla en diversas proporciones. Para modelar el comportamiento del suelo de manera precisa, es esencial representar su estructura como una combinación de estas componentes.
La forma más sencilla de determinar la proporción en la que está compuesta una muestra particular es calculando la masa de cada componente en relación con la masa total. Para lograrlo, es necesario separar físicamente cada muestra en sus componentes individuales, aprovechando las diferencias en tamaño entre ellos. Después de secar y triturar el suelo, se lleva a cabo un proceso de tamizado utilizando múltiples tamices de diferentes tamaños, seleccionados según la precisión requerida:
La imagen ilustra un esquema que separa tres componentes, que podrían corresponder a las medidas de arena, limo y arcilla. No obstante, es posible utilizar varios tamices para distinguir, por ejemplo, arena gruesa, arena media y arena fina, según sea necesario.
Las principales masas son por ello:
• la masa seca de arena en la muestra ($M_a$): Masa de todos los granos de arena.
• la masa seca de limo en la muestra ($M_i$): Masa de todos los granos de limo.
• la masa seca de arcilla en la muestra ($M_c$): Masa de todos los granos de arcilla.
ID:(2067, 0)
Distribución de arena, limo y arcilla
Concepto
Un diagrama ternario es una representación gráfica que se utiliza para mostrar las proporciones relativas de tres componentes, como el limo, la arena y la arcilla. En este diagrama, cada esquina está dedicada a uno de estos componentes, y varios puntos dentro del espacio triangular representan combinaciones únicas de estos constituyentes.
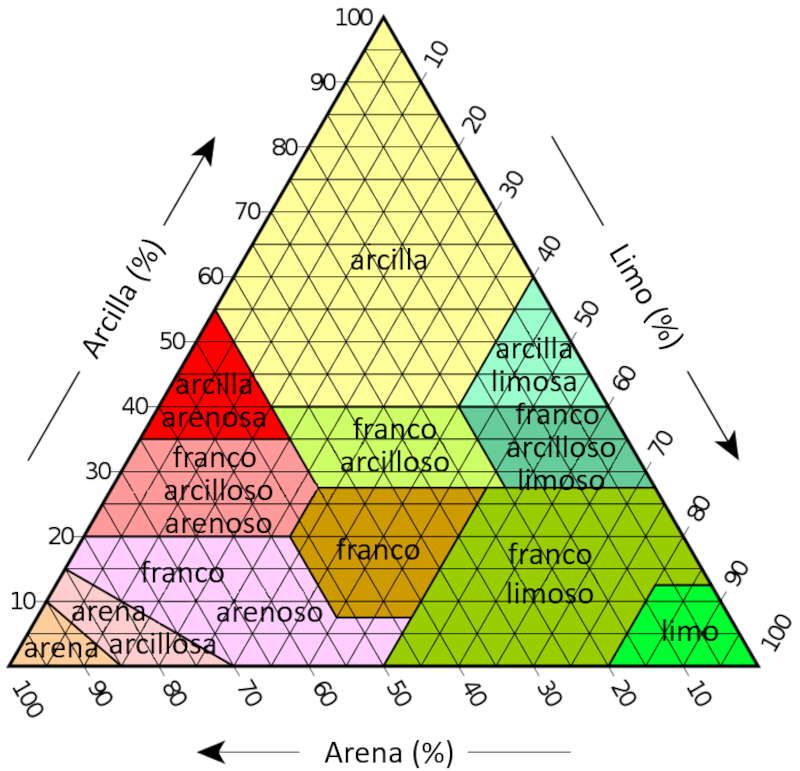
Para interpretar un diagrama ternario para el limo, la arena y la arcilla:
1. Identifica la ubicación de los componentes:
- La arena generalmente se encuentra en la esquina inferior izquierda.
- El limo se sitúa en la esquina inferior derecha.
- La arcilla está en la esquina superior.
2. Analiza las mezclas:
- Los puntos dentro del triángulo denotan diversas combinaciones de estos tres componentes.
3. Comprende las líneas y zonas:
- Las líneas que atraviesan el triángulo representan proporciones constantes de los tres componentes.
- Diferentes regiones dentro del triángulo corresponden a clasificaciones de suelos específicas.
En particular, para las zonas especificadas, se pueden estimar los siguientes rangos:
| Tipo | $g_a$ | $g_i$ | $g_c$ |
| Arcilla | 0-45 | 0-40 | 55-100 |
| Marga | 23-53 | 28-50 | 40-60 |
| Arena | 85-100 | 0-15 | 0-10 |
| Limo | 0-20 | 87-100 | 0-12 |
| Arcilla limosa | 70-90 | 0-35 | 0-15 |
| Arcilla arenosa | 45-80 | 0-28 | 20-35 |
| Franco arcilloso | 45-65 | 0-20 | 35-55 |
| Franco arcilloso limoso | 0-50 | 50-87 | 0-27 |
| Franco arcilloso arenoso | 0-20 | 40-72 | 28-40 |
| Franco limoso | 0-20 | 40-60 | 40-60 |
| Franco arenoso | 20-45 | 15-53 | 28-40 |
| Arena arcillosa | 45-85 | 0-50 | 0-20 |
en donde cualquier punto tiene que satisfacer la condición
| $ g_a + g_i + g_c = 1$ |
ID:(2070, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ g_a + g_i + g_c = 1$
g_a + g_i + g_c = 1
$ g_a =\displaystyle\frac{ M_a }{ M_s }$
g_a = M_a / M_s
$ g_c =\displaystyle\frac{ M_c }{ M_s }$
g_c = M_c / M_s
$ g_i =\displaystyle\frac{ M_i }{ M_s }$
g_i = M_i / M_s
$ M_s = M_a + M_l + M_c $
M_s = M_a + M_l + M_c
$ N_a = \displaystyle\frac{ M_a }{ m_a }$
N_a = M_a / m_a
$ N_c = \displaystyle\frac{ M_c }{ m_c }$
N_c = M_c / m_c
$ N_i = \displaystyle\frac{ M_i }{ m_i }$
N_i = M_i / m_i
$ \rho_p = \rho_a g_a + \rho_i g_i + \rho_c g_c $
rho_p = rho_a * g_a + rho_i * g_i + rho_c * g_c
$ \rho_s = \displaystyle\frac{ M_s }{ V_s }$
rho_s = M_s / V_s
$ V_a =\displaystyle\frac{ M_a }{ \rho_a }$
V_a = M_a / rho_a
$ V_a = N_a v_a $
V_a = N_a * v_a
$ V_c =\displaystyle\frac{ M_c }{ \rho_c }$
V_c = M_c / rho_c
$ V_c = N_c v_c $
V_c = N_c * v_c
$ V_i =\displaystyle\frac{ M_i }{ \rho_i }$
V_i = M_i / rho_i
$ V_i = N_i v_i $
V_i = N_i * v_i
$ V_s = V_a + V_l + V_c $
V_s = V_a + V_l + V_c
$\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$
1/ rho_s = g_a / rho_a + g_i / rho_i + g_c / rho_c
ID:(15216, 0)
Masa seca total de la muestra
Ecuación
Durante el análisis de una muestra, el primer paso implica la eliminación del agua contenida para prevenir su influencia. De esta manera, obtenemos la masa seca total de la muestra ($M_s$), que corresponde a la suma de la masa seca de arena en la muestra ($M_a$), la masa seca de limo en la muestra ($M_i$) y la masa seca de arcilla en la muestra ($M_c$):
| $ M_s = M_a + M_l + M_c $ |
Es importante enfatizar que esta masa debe estar completamente seca, ya que la humedad puede distorsionar el peso de cada componente. Además, cualquier componente como rocas y material orgánico que no sea arena, limo ni arcilla debe ser eliminado de la muestra.
ID:(4729, 0)
Fracción de arena en la muestra
Ecuación
Para describir el modelo del suelo, primero debemos entender su composición. Para ello, introducimos la variable que representa la fracción de masa de arena en la muestra ($g_a$). Esta fracción se calcula a partir de la masa seca de arena en la muestra ($M_a$) y la masa seca total de la muestra ($M_s$), utilizando la siguiente relación:
| $ M_s = M_a + M_l + M_c $ |
Esta relación se expresa de la siguiente manera:
| $ g_a =\displaystyle\frac{ M_a }{ M_s }$ |
ID:(4716, 0)
Fracción de limo en la muestra
Ecuación
Para describir el modelo del suelo, primero debemos entender su composición. Para ello, introducimos la variable que representa la fracción de masa de limo en la muestra ($g_i$). Esta fracción se calcula a partir de la masa seca de limo en la muestra ($M_i$) y la masa seca total de la muestra ($M_s$), utilizando la siguiente relación:
| $ M_s = M_a + M_l + M_c $ |
Esta relación se expresa de la siguiente manera:
| $ g_i =\displaystyle\frac{ M_i }{ M_s }$ |
ID:(15064, 0)
Fracción de arcilla en la muestra
Ecuación
Para describir el modelo del suelo, primero debemos entender su composición. Para ello, introducimos la variable que representa la fracción de masa de arcilla en la muestra ($g_c$). Esta fracción se calcula a partir de la masa seca de arcilla en la muestra ($M_c$) y la masa seca total de la muestra ($M_s$), utilizando la siguiente relación:
| $ M_s = M_a + M_l + M_c $ |
Esta relación se expresa de la siguiente manera:
| $ g_c =\displaystyle\frac{ M_c }{ M_s }$ |
ID:(15065, 0)
Condición de normalización
Ecuación
Dado que las la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$) se calculan en función de su proporción en relación a las masas respectivas de la masa seca de arena en la muestra ($M_a$), la masa seca de limo en la muestra ($M_i$) y la masa seca de arcilla en la muestra ($M_c$) en la muestra, que suman las la masa total ($M_t$) con las que se normaliza:
| $ M_s = M_a + M_l + M_c $ |
Obtenemos una condición de normalización:
| $ g_a + g_i + g_c = 1$ |
Si sumamos la fracción de masa de arena en la muestra ($g_a$) en la muestra:
| $ g_a =\displaystyle\frac{ M_a }{ M_s }$ |
junto con la fracción de masa de limo en la muestra ($g_i$) en la muestra:
| $ g_i =\displaystyle\frac{ M_i }{ M_s }$ |
y la fracción de masa de arcilla en la muestra ($g_c$) en la muestra:
| $ g_c =\displaystyle\frac{ M_c }{ M_s }$ |
obtenemos:
$g_a + g_i + g_c = \displaystyle\frac{M_a}{M_t} + \displaystyle\frac{M_i}{M_t} + \displaystyle\frac{M_c}{M_t} = \displaystyle\frac{M_a + M_i + M_c}{M_t}$
Dado que se cumple la condición de que $M_t$ es la masa total:
| $ M_s = M_a + M_l + M_c $ |
esto resulta en:
| $ g_a + g_i + g_c = 1$ |
ID:(15072, 0)
Número de granos de arenas de la muestra
Ecuación
Para modelar el suelo, es fundamental introducir la variable que corresponde a el número de granos de arena en la muestra ($N_a$), la cual se puede calcular dividiendo la masa seca de arena en la muestra ($M_a$) entre la masa de un grano de arena ($m_a$):
| $ N_a = \displaystyle\frac{ M_a }{ m_a }$ |
ID:(1539, 0)
Número de granos de limo de la muestra
Ecuación
Para modelar el suelo, es fundamental introducir la variable que corresponde a el número de granos de limo en la muestra ($N_i$), la cual se puede calcular dividiendo la masa seca de limo en la muestra ($M_i$) entre la masa de un grano de limo ($m_i$):
| $ N_i = \displaystyle\frac{ M_i }{ m_i }$ |
ID:(15067, 0)
Número de granos de arcilla de la muestra
Ecuación
Para modelar el suelo, es fundamental introducir la variable que corresponde a el número de granos de arcilla en la muestra ($N_c$), la cual se puede calcular dividiendo la masa seca de arcilla en la muestra ($M_c$) entre la masa de una plaquita de arcilla ($m_c$):
| $ N_c = \displaystyle\frac{ M_c }{ m_c }$ |
ID:(15068, 0)
Volumen de la componente de arena de la muestra
Ecuación
Para modelar el comportamiento del suelo, es necesario introducir la variable que corresponde a el volumen sólido de arena ($V_a$). Esta variable se puede calcular a partir de el número de granos de arena en la muestra ($N_a$) y el volumen de un grano de arena ($v_a$) mediante la siguiente ecuación:
| $ V_a = N_a v_a $ |
Si modelamos el grano como una esfera con radio $r_a$, podemos calcular su volumen utilizando la fórmula:
| $ v_a =\displaystyle\frac{4 \pi }{3} r_a ^3$ |
Con la densidad de la arena $\rho_a$, podemos determinar la masa de un solo grano de arena mediante la ecuación:
| $ m_a = \rho_a v_a $ |
Al dividir la masa de la muestra de arena $M_a$ por la masa de un solo grano, podemos obtener el número de granos:
| $ N_a = \displaystyle\frac{ M_a }{ m_a }$ |
Esto nos permite calcular el volumen de la componente de arena:
| $ V_a = N_a v_a $ |
ID:(10366, 0)
Volumen de la componente de limo de la muestra
Ecuación
Para modelar el comportamiento del suelo, es necesario introducir la variable que corresponde a el volumen sólido de limo ($V_i$). Esta variable se puede calcular a partir de el número de granos de limo en la muestra ($N_i$) y el volumen de un grano de limo ($v_i$) mediante la siguiente ecuación:
| $ V_i = N_i v_i $ |
Si modelamos el grano como una esfera con radio $r_i$, podemos calcular su volumen utilizando la fórmula:
| $ v_i = a_i ^3$ |
Con la densidad de la limo $\rho_i$, podemos determinar la masa de un solo grano de limo mediante la ecuación:
| $ m_i = \rho_i v_i $ |
Al dividir la masa de la muestra de limo $M_i$ por la masa de un solo grano, podemos obtener el número de granos:
| $ V_c = N_c v_c $ |
Esto nos permite calcular el volumen de la componente de limo:
| $ V_i = N_i v_i $ |
ID:(10365, 0)
Volumen de la componente de arcilla de la muestra
Ecuación
Para modelar el comportamiento del suelo, es necesario introducir la variable que corresponde a el volumen sólido de arcilla ($V_c$). Esta variable se puede calcular a partir de el número de granos de arcilla en la muestra ($N_c$) y el volumen de un grano de arcilla ($v_c$) mediante la siguiente ecuación:
| $ V_c = N_c v_c $ |
Si modelamos el grano como una delgada placa con longitud y ancho $l_c$ y altura $w_c$, podemos calcular su volumen utilizando la fórmula:
| $ v_c = w_c l_c ^2$ |
Con la densidad de la arcilla representada por $\rho_c$, podemos determinar la masa de un solo grano de arcilla mediante la siguiente ecuación:
| $ m_c = \rho_c v_c $ |
Al dividir la masa de la muestra de arcilla $M_c$ por la masa de un solo grano, podemos obtener el número de granos:
| $ N_c = \displaystyle\frac{ M_c }{ m_c }$ |
Esto nos permite calcular el volumen del componente de arcilla:
| $ V_c = N_c v_c $ |
ID:(15069, 0)
Cálculo directo volumen de arena de la muestra
Ecuación
Utilizando la definición de densidad, es posible calcular el el volumen sólido de arena ($V_a$) directamente a partir de la la masa seca de arena en la muestra ($M_a$) y la densidad de un grano de arena ($\rho_a$) mediante la siguiente fórmula:
| $ V_a =\displaystyle\frac{ M_a }{ \rho_a }$ |
Este cálculo directo presenta la ventaja de que no depende de la forma de los granos:
Si asumimos que la densidad es homogénea, podemos calcular el volumen total de manera independiente del número y la forma de los granos.
ID:(3168, 0)
Cálculo directo volumen de limo de la muestra
Ecuación
Utilizando la definición de densidad, es posible calcular el el volumen sólido de limo ($V_i$) directamente a partir de la la masa seca de limo en la muestra ($M_i$) y la densidad de un grano de limo ($\rho_i$) mediante la siguiente fórmula:
| $ V_i =\displaystyle\frac{ M_i }{ \rho_i }$ |
Este cálculo directo presenta la ventaja de que no depende de la forma de los granos:
Si asumimos que la densidad es homogénea, podemos calcular el volumen total de manera independiente del número y la forma de los granos.
ID:(15070, 0)
Cálculo directo volumen de arcilla de la muestra
Ecuación
Utilizando la definición de densidad, es posible calcular el el volumen sólido de arcilla ($V_c$) directamente a partir de la la masa seca de arcilla en la muestra ($M_c$) y la densidad de un grano de arcilla ($\rho_c$) mediante la siguiente fórmula:
| $ V_c =\displaystyle\frac{ M_c }{ \rho_c }$ |
Este cálculo directo presenta la ventaja de que no depende de la forma de los granos:
Si asumimos que la densidad es homogénea, podemos calcular el volumen total de manera independiente del número y la forma de los granos.
ID:(15071, 0)
Volumen sólido de componentes
Ecuación
Una vez que conocemos energía de Electrones ($E$), susceptibles Totales al tiempo $t$ ($S_t$) y infectados Totales al tiempo $t$ ($I_t$), podemos calcular el volumen sólido de una componente ($V_s$) sumando las diferentes componentes, como se describe en la siguiente ecuación:
| $ V_s = V_a + V_l + V_c $ |
ID:(4734, 0)
Densidad sólida
Ecuación
Dado que ya conocemos la masa seca total de la muestra ($M_s$) y el volumen sólido ($V_s$) de la muestra, podemos introducir la densidad sólida ($\rho_s$) y calcularlo utilizando la siguiente ecuación:
| $ \rho_s = \displaystyle\frac{ M_s }{ V_s }$ |
ID:(15073, 0)
Calculo de la densidad sólida desde las fracciones
Ecuación
La densidad sólida ($\rho_s$) se puede calcular a partir de la densidad de un grano de arena ($\rho_a$), la densidad de un grano de limo ($\rho_i$) y la densidad de un grano de arcilla ($\rho_c$), así como de los factores que describen su composición: la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$) y la fracción de masa de arcilla en la muestra ($g_c$). Esto nos lleva a la siguiente relación:
| $\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$ |
Si expresamos el inverso de la densidad sólida ($\rho_s$) definida en la masa seca total de la muestra ($M_s$) y el volumen sólido ($V_s$) mediante la ecuación:
| $ \rho_s = \displaystyle\frac{ M_s }{ V_s }$ |
Y considerando que el volumen sólido es la suma de el volumen sólido de arena ($V_a$), el volumen sólido de limo ($V_i$), y el volumen sólido de arcilla ($V_c$):
| $ V_s = V_a + V_l + V_c $ |
Obtenemos:
$\displaystyle\frac{1}{\rho_s}=\displaystyle\frac{V_s}{M_s}=\displaystyle\frac{V_a+V_i+V_c}{M_s}$
Sustituyendo los volúmenes con las relaciones para la densidad de un grano de arena ($\rho_a$)
| $ V_a =\displaystyle\frac{ M_a }{ \rho_a }$ |
de la densidad de un grano de limo ($\rho_i$)
| $ V_i =\displaystyle\frac{ M_i }{ \rho_i }$ |
y la densidad de un grano de arcilla ($\rho_c$)
| $ V_c =\displaystyle\frac{ M_c }{ \rho_c }$ |
Obtenemos:
$\displaystyle\frac{1}{\rho_s}=\displaystyle\frac{1}{\rho_a}\displaystyle\frac{M_a}{M_s}+\displaystyle\frac{1}{\rho_i}\displaystyle\frac{M_i}{M_s}+\displaystyle\frac{1}{\rho_c}\displaystyle\frac{M_c}{M_s}$
Con la fracción de masa de arena en la muestra ($g_a$)
| $ g_a =\displaystyle\frac{ M_a }{ M_s }$ |
para la fracción de masa de limo en la muestra ($g_i$)
| $ g_i =\displaystyle\frac{ M_i }{ M_s }$ |
y la fracción de masa de arcilla en la muestra ($g_c$)
| $ g_c =\displaystyle\frac{ M_c }{ M_s }$ |
Obtenemos:
| $\displaystyle\frac{1}{ \rho_s }=\displaystyle\frac{ g_a }{ \rho_a }+\displaystyle\frac{ g_i }{ \rho_i }+\displaystyle\frac{ g_c }{ \rho_c }$ |
ID:(15074, 0)
Densidad de partícula
Ecuación
La densidad de partícula ($\rho_p$) se puede calcular como la densidad promedio en la que los factores de ponderación son los componentes. Por lo tanto, con la fracción de masa de arena en la muestra ($g_a$), la fracción de masa de limo en la muestra ($g_i$), la fracción de masa de arcilla en la muestra ($g_c$) y la densidad de un grano de arena ($\rho_a$), la densidad de un grano de limo ($\rho_i$), la densidad de un grano de arcilla ($\rho_c$), se puede definir de la siguiente manera:
| $ \rho_p = \rho_a g_a + \rho_i g_i + \rho_c g_c $ |
ID:(15127, 0)