Componentes del Suelo
Storyboard 
Las tres componentes fundamentales del suelo son la arena, el limo y la arcilla. Mientras que los granos de arena y limo tienen una forma relativamente esférica, la arcilla se asemeja más a pequeñas plaquitas. Además, existe una notable diferencia en sus tamaños: los granos de arena son solo una fracción de milímetro, los granos de limo tienen dimensiones del orden de micrones, y la arcilla consiste en partículas aún más diminutas, de unos pocos micrones.
Esta variación en los tamaños de partículas tiene un impacto significativo en la capacidad del suelo para compactarse. La arcilla, por ejemplo, puede llenar los espacios intersticiales entre los granos de arena y limo, lo que influye en los diferentes grados de compactación que se pueden lograr en el suelo.
ID:(362, 0)
Suelo superficial
Concepto 
Cuando observamos la superficie del suelo, con frecuencia encontramos algunas bolos, guijarros, piedrecillas, una masa de color marrón que llamamos suelo y algunas plantas.

Campo en el paraje 'Bising' cerca del pueblo de Oberwilzingen, en la Selva Negra, por Ustill (commons.wikimedia.org).
Sin embargo, si observamos con mayor atención, notaremos que el suelo contiene restos de plantas, desde piedras más pequeñas hasta granos de arena. Estos restos de plantas descompuestas corresponden a material orgánico de menor tamaño que a veces se confunde con el suelo circundante.
En resumen, podemos identificar:
• Bolos, guijarros, piedrecillas
• Materia orgánica presente en el suelo.
• El propio suelo en sí.
ID:(15075, 0)
Bolos, guijarros, piedrecillas
Concepto 
En todos os tipos de solo, encontramos pedras grandes, seixos e pequenas pedras distribuídos em várias profundidades. Da mesma forma, à medida que o solo é erodido na superfície, essas pedras tendem a permanecer nela, uma vez que o solo ao seu redor foi lavado por fluxos superficiais de água.

Guijarros en una playa de Broulee, Australia, por Steve Shattuck (commons.wikimedia.org)
A concentração de pedras grandes, seixos e pequenas pedras varia e afeta as propriedades mecânicas e hidrodinâmicas do solo. Por um lado, as rochas no interior estabilizam o solo, conferindo-lhe maior resistência à deformação. Por outro lado, devido à falta de porosidade, elas obstruem o fluxo de água, afetando o transporte de umidade por difusão. Nesse sentido, o papel das pedras deve ser levado em consideração na modelagem do solo.
ID:(15077, 0)
Materia orgánica
Concepto 
En los poros del suelo superficial, se encuentra materia orgánica que consiste en residuos de plantas y animales, biomasa microbiana, humus y materia exudada por las raíces.

Guía de bricolaje para microscopía de suelos agrícolas, Katelyn Solbakk, Mikroliv, Okologisk Landsforening
Dentro de la biomasa microbiana, encontramos microorganismos como bacterias y hongos. Por otro lado, el humus es un material orgánico altamente descompuesto que proviene de restos vegetales y microbianos. El humus mejora significativamente la capacidad del suelo para retener nutrientes y agua.
ID:(15078, 0)
Suelo en profundidad
Concepto 
Cuando observamos un corte en el suelo, en la superficie vemos la cobertura vegetal, y debajo encontramos las raíces que penetran los primeros centímetros del suelo, que contiene materia orgánica. Por materia orgánica entendemos material en descomposición, organismos y microorganismos que viven en entornos acuosos, por lo que se encuentran en los poros del suelo donde se encuentra el agua.

Corte de suelo en Palos Verdes, Chaihuin, Chile por W.Gerber
Si observamos en las capas inferiores, notamos que la materia orgánica comienza a desaparecer y vemos el suelo en sí, con sus tres componentes: arena, limo y arcilla, así como rocas. La concentración de estas distintas componentes varía, creando diferentes capas con propiedades físicas y capacidad de absorción y transporte de agua diversas.
En resumen, en el suelo podemos identificar componentes distintas a la materia orgánica y las rocas principales:
• Arena
• Limo
• Arcilla
ID:(15076, 0)
Arena
Concepto 
La arena fina es un tipo de partícula de suelo caracterizada por su tamaño relativamente pequeño. Se encuentra entre las partículas más gruesas de arena y las partículas más finas de limo en términos de tamaño. Las partículas de arena fina suelen tener un tamaño que va desde 0.02 hasta 0.2 milímetros o de 20 a 200 micrómetros.
La arena fina se encuentra comúnmente en la composición del suelo y se caracteriza por su capacidad para retener cierta cantidad de humedad mientras permite un drenaje razonable. Puede contribuir a la textura del suelo y afectar su capacidad para soportar el crecimiento de las plantas. El suelo con una mayor proporción de arena fina tiende a tener buenas propiedades de aireación y drenaje.

Dunas de Erg Awbari (Idehan Ubari) en la región del desierto del Sahara, en el Distrito de Wadi Al Hayaa, en la región de Fezzan, en el suroeste de Libia, por Luca Galuzzi (commons.wikimedia.org).
La composición química de la arena puede variar según su origen y composición mineral. La arena generalmente está compuesta por varios minerales, siendo el cuarzo uno de los más comunes. Sin embargo, la composición química exacta de la arena puede variar ampliamente. Aquí tienes una visión general de la composición química de la arena, con rangos aproximados en porcentaje:
• Quarzo (SiO_2) 90% - 95% [1]: El dióxido de silicio, comúnmente conocido como sílice, es el componente principal de la mayoría de las arenas. Puede constituir entre un 60% y un 95% o más de la composición de la arena.
• Feldespato (KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8) <10% [1]: El feldespato es otro mineral común en la arena, y su composición puede variar. El feldespato potásico (K-feldespato), el feldespato sódico (Na-feldespato) y el feldespato cálcico (Ca-feldespato) son diferentes tipos de minerales de feldespato que se encuentran en la arena.
• Mica (Muscovita, Biotita) <5% [1]: Los minerales de mica, como la muscovita y la biotita, pueden variar entre el 1% y el 5% o menos de la composición del limo.
• Otros Minerales: Dependiendo de la fuente geológica de la arena, esta puede contener trazas de otros minerales, como feldespato, mica o magnetita.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2080, 0)
Limo
Concepto 
El limo es un tipo de partícula de suelo que se encuentra entre la arena y la arcilla en términos de tamaño de partícula. Las partículas de limo generalmente tienen un tamaño que oscila entre 0.002 y 0.02 milímetros, lo que equivale a 2 a 20 micrómetros. Estas partículas son más pequeñas que las de arena pero más grandes que las de arcilla.
Una característica distintiva del limo es su capacidad para retener la humedad y los nutrientes, lo que lo convierte en un suelo adecuado para la agricultura. Sin embargo, es importante tener en cuenta que el limo puede compactarse y presentar problemas de drenaje si predomina en la composición del suelo. Los suelos con contenido de limo suelen ser fértiles y pueden sustentar una variedad de cultivos cuando se manejan adecuadamente.

Acumulación de limo en Zimbabue por MaRally (commons.wikimedia.org)
La composición química del limo puede variar según su origen y ubicación geográfica. Sin embargo, en términos generales, el limo está compuesto por varios minerales y puede contener materia orgánica. A continuación, proporciono una aproximación de la composición química del limo en términos de los principales elementos, expresados como porcentaje de la composición total:
• Quarzo (SiO_2) 40-60% [1]: El cuarzo suele ser el mineral dominante en el limo, representando aproximadamente entre el 50% y el 70% o incluso más de su composición.
• Feldespato (KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8) <10% [1]: Los minerales de feldespato, que incluyen feldespato potásico, feldespato sódico y feldespato cálcico, pueden variar desde un 10% hasta un 30% o más de la composición.
• Mica (Muscovita, Biotita) < 5% [1]: Los minerales de mica, como la muscovita y la biotita, pueden variar entre el 1% y el 5% o menos de la composición del limo.
• Otros Minerales: El limo puede contener trazas de varios otros minerales según su origen geológico específico, como circón, granate y otros.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2068, 0)
Arcilla
Concepto 
La arcilla es un tipo de partícula de suelo con partículas muy finas, típicamente más pequeñas de 0.002 milímetros de tamaño o menos de 2 micrómetros. Las partículas de arcilla son mucho más pequeñas que las partículas de arena y limo. Los suelos arcillosos son conocidos por su capacidad para retener agua y nutrientes debido a su pequeño tamaño de partícula y alta área superficial. Sin embargo, también pueden compactarse fácilmente y pueden tener propiedades de drenaje deficientes. Los suelos arcillosos pueden variar en color y textura según su composición mineral y contenido de materia orgánica. Son un componente importante de muchos tipos de suelos y pueden influir en la fertilidad y estructura del suelo.

NoneArcilla cuaternaria en Estonia (400 000 años de antigüedad) por Siim Sepp (commons.wikimedia.org)
La composición química de la arcilla puede variar según su composición mineral específica y su origen. La arcilla está compuesta principalmente por diminutas partículas minerales y generalmente consiste en varios minerales, que incluyen:
• Caolinita (Al_2Si_2O_5(OH)_4) 20-40% [1]: La caolinita es un mineral de arcilla común y el principal componente de la arcilla de caolín.
• Illita ((K, H_3O)(Al, Mg, Fe)_2(Si, Al)_4O_{10}[(OH)_2,(H_2O)]) 10-40% [1]: La illita es otro mineral de arcilla común.
• Esmectitas/Montmorillonita ((Na, Ca)_{0.33}(Al, Mg)_2(Si_4O_{10})(OH)_2·n(H_2O)) 10-40% [1]: La montmorillonita es un mineral de arcilla conocido por sus propiedades de hinchamiento.
• Clorita ((Mg, Fe)_3(Si, Al)_4O_{10}(OH)_2·(Mg, Fe)_3(OH)_6) <10% [1]: A veces, se encuentra clorita en minerales de arcilla.
• Otros Minerales: Además, dependiendo del depósito de arcilla específico, otros minerales también pueden estar presentes en cantidades mínimas, incluyendo cuarzo, feldespato y varios óxidos metálicos.
[1] Clay Mineralogy, Ralph E. Grim, McGraw-Hill International Series
ID:(2069, 0)
Forma de granos
Concepto 
Para modelar el suelo de manera efectiva, es fundamental considerar las formas geométricas que mejor describen los diversos tipos de granos que componen el suelo.
Para ello, se deben observar múltiples granos de cada tipo. En el caso de la arena, esto es posible bajo un microscopio normal y permite obtener colecciones de granos como la que se observa a continuación:

Granos de arena de arena de construcción amarilla. Microscopio Lumam R-8. Iluminación EPI. La foto de cada grano de arena es el resultado de apilamiento multifocal realizado por Alexander Klepnev (commons.wikimedia.org).
En este caso, podemos concluir que la forma es redondeada, por lo que se les puede representar efectivamente como esferas.
ID:(2257, 0)
Formación de Granos de Arena y Limo
Concepto 
Por lo general, los granos de arena y granos de limo son conglomerados de múltiples cristales que están expuestos a impactos a medida que son transportados por el agua o el viento. Estos impactos generan fracturas a lo largo de los planos del cristal, eliminando fragmentos sobresalientes y, como resultado, redondeando el grano:
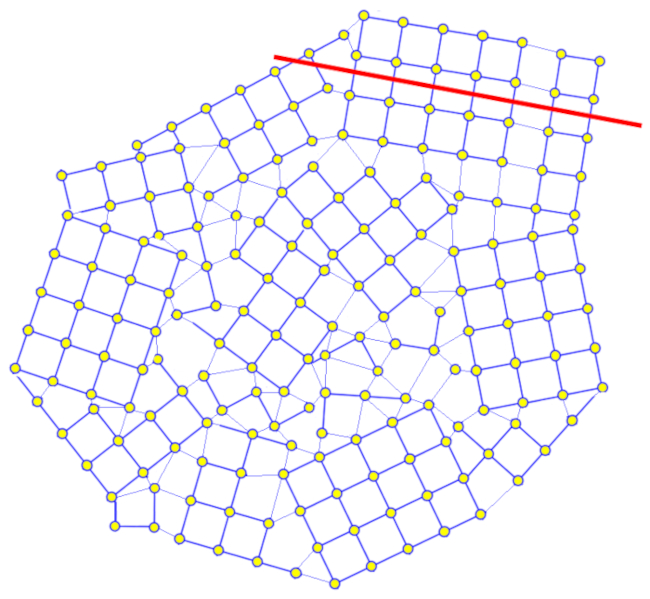
El grano se redondea a medida que sus esquinas se desgastan gradualmente.
De esta manera, tienden a volverse más redondeados y adquieren una forma que se asemeja a pequeñas esferas.
ID:(2081, 0)
Formación de Granos de Arcilla
Concepto 
Los granos de arcilla suelen ser pequeños cristales que están expuestos a impactos a medida que son transportados por el agua o el viento. Estos impactos generan fracturas a lo largo de los planos del cristal, lo que, dado que el grano es un cristal, implica que mantenga su forma sin redondear las esquinas:
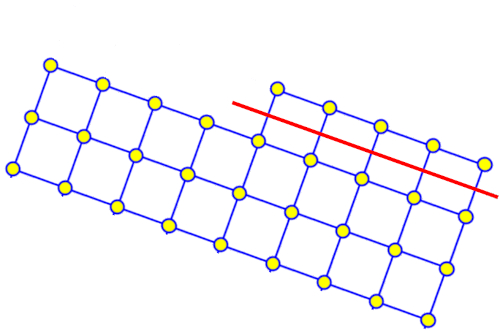
El grano mantiene su forma ya que tiende a desgastarse gradualmente en el mismo plano que define su forma.
Por lo tanto, los granos de arcilla se caracterizan por tener una forma geométrica similar a pequeñas placas que se asemejan a paralelepípedos rectos.
ID:(2083, 0)
Forma del granos de arena
Concepto 
Si observamos los granos bajo un microscopio, notaremos que tienen formas relativamente redondeadas y tamaños variables, aunque tienden a ser de un tamaño similar:

Granos de la llamada 'Arena de Sílice de Ottawa' bajo un microscopio electrónico. Aumento de 150x. La 'Arena de Ottawa' es un subproducto de la minería hidráulica de orto-cuarzos ordovicianos de la Formación de la Arenisca de San Pedro en la Cuenca de Illinois intracratónica del Paleozoico por la NASA (commons.wikimedia.org)
Por lo tanto, en una primera aproximación, los granos pueden ser modelados como esferas:
Los granos de arena pueden modelarse como esferas. Para simplificar el modelo, se asume que todos son iguales. Sin embargo, un modelo más detallado podría considerar la distribución de radios diversos.
En línea con la hipótesis inicial de que los granos de arena se pueden modelar como esferas, se puede introducir su correspondiente radio.
Por lo tanto, introducimos el radio el radio del grano de arena (r_a) para describir las esferas de los granos de arena.
Debe tenerse presente que el radio es un valor medio, dado que varia entre los distintos granos.
ID:(15054, 0)
Forma del grano de limo
Concepto 
Si observamos los granos de limo bajo un microscopio, notaremos que tienen formas relativamente cubicas y tamaños variables, aunque tienden a ser de un tamaño similar:

Initial silt Proctor compaction at optimum wtare content - high magnification, Scanning Electron Microscope (SEM) investigations in soil microstructure description, Dimitri Deneele, 1st IMEKO TC-4 International Workshop on Metrology for Geotechnics, Benevento, Italy, March 17-18, 2016
Por lo tanto, en una primera aproximación, los granos pueden ser modelados como cubos:
Los granos de limo pueden modelarse como cubos. Para simplificar el modelo, se asume que todos son iguales. Sin embargo, un modelo más detallado podría considerar la distribución de lados diversos.
En línea con la hipótesis inicial de que los granos de limo se pueden modelar como cubos, se puede introducir su correspondiente lado.
Por lo tanto introducimos el lado del cubo el lado del grano de limo (a_i) para describir los granos de limo.
Debe tenerse presente que el lado es un valor medio, dado que varia entre los distintos granos.
ID:(15056, 0)
Forma del grano de arcilla
Concepto 
Los granos de arcilla son relativamente planos y tienden a apilarse en forma paralela, como se puede apreciar en esta imagen obtenida mediante un microscopio electrónico:

SEM image of well crystallized crystallizedkaolinite from sandstone. Note hexagonal morphology,smooth basal surfaces and abundance of slit- andwedge-shaped pores. (The influence of individual clay minerals on formation damage of reservoir sandstones: A critical review with some new insights, Jeff Wilson, L. Wilson, Ian T.M. Patey, May 2014Clay Minerals 49(2))
Su forma se asemeja a elementos planos de grosor reducido que se parecen a paralelepípedos rectos:
Los granos de arcilla pueden modelarse como paralelepípedos rectos. Para simplificar el modelo, se asume que todos son iguales. Sin embargo, un modelo más detallado podría considerar la distribución de longitudes y alturas diversas.
En línea con la hipótesis inicial de que los granos de arcilla se pueden modelar como paralelepípedos rectos, se pueden introducir sus correspondientes longitudes y altura.
Por lo tanto se introduce para describir el paralelepipedo recto el largo y ancho de una plaquita de arcilla (l_c) y la altura de una plaquita de arcilla (w_c).
Debe tenerse presente que las longitudes y la altura son valores medios, dado que en realidad varían entre los distintos granos.
ID:(15055, 0)
Densidad del grano de arena
Variable 
Para calcular la masa de un grano de arena, es esencial conocer su densidad. Sin embargo, es importante destacar que la densidad del grano en sí difiere significativamente de la densidad de la arena en su conjunto, debido a la presencia de una alta porosidad en esta última. Por lo tanto, para estimar la densidad de un grano de arena, se debe analizar la densidad de sus minerales principales, que se detallan a continuación:
| Mineral | Ocurrencia | Densidad [g/cm^3] |
| Quarzo | 90-95% [1] | 2.65 [2] |
| Feldspars | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Para desarrollar un modelo simple, se puede asumir una densidad homogénea:
Si suponemos que los minerales de los que están compuestos los granos de arena están distribuidos de manera homogénea, podemos asumir que los granos tienen una densidad constante y uniforme en todos ellos.
Con ello se introduce la densidad de un grano de arena (\rho_a).
Es importante tener presente que valor puede variar según la composición de los granos de arena.
ID:(15057, 0)
Densidad de un grano de limo
Variable 
Para calcular la masa de un grano de limo, es esencial conocer su densidad. Sin embargo, es importante destacar que la densidad del grano en sí difiere significativamente de la densidad del limo en su conjunto, debido a la presencia de una alta porosidad en esta última. Por lo tanto, para estimar la densidad de un grano de limo, se debe analizar la densidad de sus minerales principales, que se detallan a continuación:
| Mineral | Ocurrencia | Densidad [g/cm^3] |
| Quarzo | 40-60% [1] | 2.65 [2] |
| Feldspars | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Para desarrollar un modelo simple, se puede asumir una densidad homogénea:
Si suponemos que los minerales de los que están compuestos los granos de limo están distribuidos de manera homogénea, podemos asumir que los granos tienen una densidad constante y uniforme en todos ellos.
Con ello se introduce la densidad de un grano de limo (\rho_i).
Es importante tener presente que valor puede variar según la composición de los granos de limo.
ID:(15059, 0)
Densidad de un grano de arcilla
Variable 
Para calcular la masa de un grano de arcilla, resulta fundamental conocer su densidad. No obstante, es crucial destacar que la densidad del grano en sí difiere significativamente de la densidad de arcilla en su totalidad, debido a la notable presencia de una alta porosidad en esta última. Por lo tanto, para estimar la densidad de un grano de arcilla, es necesario analizar la densidad de sus minerales principales, que se describen a continuación:
| Mineral | Ocurrencia | Densidad [g/cm^3] |
| Esmectitas | 0-80% [1] | 2.75-2.78 [2] |
| Illitas | 10-80% [1] | 2.60-2.86 [2] |
| Caolinitas | 20-80% [1] | 2.62-2.66 [2] |
| Cloritas | 0-30% [1] | 2.60-2.96 [2] |
[1] Clay Mineralogy, Ralph E. Grim (1968), McGraw-Hill
[2] Geotechnical Engineering Principles and Practices, Donald P. Coduto et al. (1998), Prentice-Hall
Para desarrollar un modelo simple, se puede asumir una densidad homogénea:
Si suponemos que los minerales de los que están compuestos los granos de arcilla están distribuidos de manera homogénea, podemos asumir que los granos tienen una densidad constante y uniforme en todos ellos.
Con ello se introduce la densidad de un grano de arcilla (\rho_c).
Es importante tener presente que este valor puede variar según la composición específica de los granos de arcilla.
ID:(15058, 0)
Carta USGS con medidas de Granos
Imagen 
El estudio de los granos en una muestra de suelo implica un análisis exhaustivo de varios aspectos que contribuyen a comprender las propiedades físicas y el comportamiento del suelo. A continuación, se presenta una explicación detallada de los componentes clave de este estudio:
Términos de Tamaño:
- Los términos de tamaño se refieren a la categorización de las partículas de suelo según su diámetro. Las partículas de suelo suelen clasificarse en tres categorías principales:
Arena: Las partículas más grandes, con diámetros que van desde 0.05 mm hasta 2 mm.
Limo: Partículas de tamaño intermedio, que van desde 0.002 mm hasta 0.05 mm.
Arcilla: Las partículas más pequeñas, con diámetros inferiores a 0.002 mm.
- Las proporciones relativas de estas fracciones de tamaño determinan la textura del suelo, lo que, a su vez, afecta sus propiedades, como la retención de agua y el drenaje.
Tamaños de Tamices:
- Los tamaños de tamices son tamaños de malla estandarizados utilizados para separar las partículas de suelo por tamaño. Los tamaños comunes de tamices están definidos por los estándares ASTM (Sociedad Estadounidense de Pruebas y Materiales) o ISO (Organización Internacional de Normalización).
- El análisis de tamices implica pasar una muestra de suelo a través de un conjunto de tamices con mallas progresivamente más finas para determinar la distribución del tamaño de las partículas.
Número de Granos por mg:
- Esta métrica representa la densidad de partículas de suelo dentro de una masa dada de suelo. Se calcula contando el número de partículas dentro de una masa conocida de suelo (generalmente 1 mg) y luego extrapolando para estimar el número total de partículas en una muestra más grande.
- Proporciona información sobre la población y el espaciado de las partículas de suelo, lo que puede ser esencial para comprender la compactación del suelo y la penetración de las raíces.
Velocidad de Sedimentación:
- La velocidad de sedimentación se refiere a la velocidad a la que las partículas de suelo caen a través de un fluido (generalmente agua) bajo la influencia de la gravedad. Esta velocidad está determinada por el tamaño, la forma y la densidad de las partículas y la viscosidad del fluido.
- El conocimiento de las velocidades de sedimentación es valioso en estudios de sedimentación y puede ayudar a predecir cuánto tiempo lleva que las partículas se sedimenten fuera de la suspensión en cuerpos de agua.
Velocidad Umbral para la Tracción:
- La velocidad umbral para la tracción representa la velocidad mínima del flujo de agua necesaria para iniciar el movimiento de partículas de suelo en el lecho de un arroyo o río. Es un parámetro importante en estudios de transporte de sedimentos.
- Cuando la velocidad del agua supera la velocidad umbral para un tamaño de partícula específico, puede erosionar y transportar esas partículas, lo que puede tener importantes implicaciones ambientales.
A modo de ejemplo, aquí se muestra la tabla de tamaños de partículas medida en el Long Island Sound por la Oficina Geológica de los Estados Unidos (USGS).
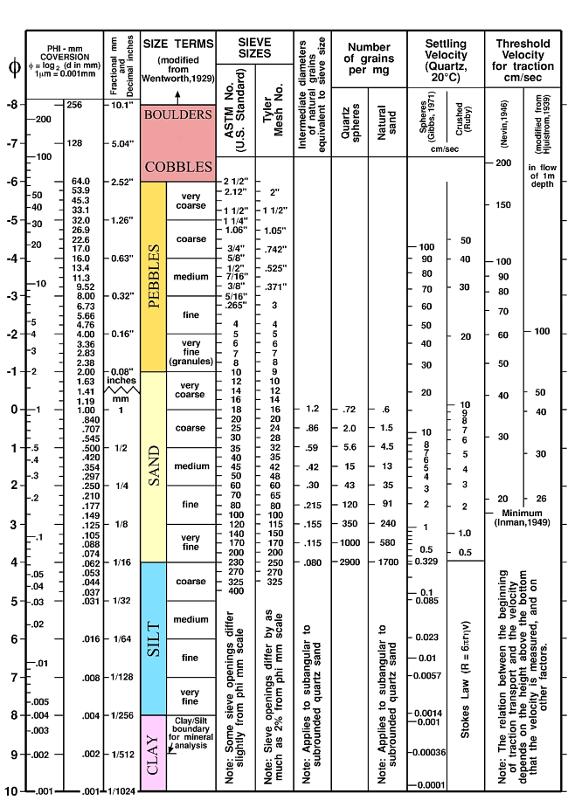
usgs-ofr-00-304
ID:(6941, 0)
Parámetros del modelo
Descripción 
El modelo se puede definir considerando tres tipos de materiales (arena, limo y arcilla), con granos modelados de la siguiente manera: en los dos primeros casos, los granos se representan como esferas con radios de diferentes tamaños, mientras que en el caso de la arcilla, los granos se modelan como paralelepípedos rectos.
Los rangos de los parámetros se resumen en la siguiente tabla:
| Tipo | Parámetro | Símbolo | Rango | Unidad |
| Arena | Radio | r_a | 62 - 2000 | \mu m |
| Volumen | v_a | 1 - 33500 | nl | |
| Densidad | \rho_a | 2.64 - 2.69 | g/cm^3 | |
| Masa | m_a | 2.6 - 90100 | \mu g | |
| Limo | Radio | r_i | 4 - 62 | \mu m |
| Volumen | v_i | 0.27 - 990 | pl | |
| Densidad | \rho_i | 2.63 - 2.72 | g/cm^3 | |
| Masa | m_i | 0.71 - 2700 | ng | |
| Arcilla | Largo | l_c | 1 - 4 | \mu m |
| Altura | w_c | 0.1 - 0.4 | \mu m | |
| Volumen | v_c | 0.1 - 6.4 | fl | |
| Densidad | \rho_c | 2.66 - 2.80 | g/cm^3 | |
| Masa | m_c | 0.27 - 17.9 | pg |
Al ser tan pequeños los granos se hace necesario trabajar en un gran rango de las dimensiones. Por ello se emplean las abreviaviaciones:
Largos
| Símbolo | Unidad | MKS |
| m | metro | 1 m |
| mm | milimetro | 10^{-3} m |
| \mu m | micrometro | 10^{-6} m |
Volumen
| Símbolo | Unidad | MKS |
| m^3 | metro cubico | 1 m^3 |
| l | litro | 10^{-3} m^3 |
| ml | mililitro | 10^{-6} m^3 |
| \mu l | microlitro | 10^{-9} m^3 |
| nl | nanolitro | 10^{-12} m^3 |
| pl | picolitro | 10^{-15} m^3 |
| fl | fentolitro | 10^{-18} m^3 |
Masa
| Símbolo | Unidad | MKS |
| kg | kilogramo | 1 kg |
| g | gramo | 10^{-3} kg |
| mg | miligramo | 10^{-6} kg |
| \mu g | microgramo | 10^{-9} kg |
| ng | nanogramo | 10^{-12} kg |
| pg | picogramo | 10^{-15} kg |
Densidad
| Símbolo | Unidad | MKS |
| kg/m^3 | kilogramo por metro cubico | 1 kg/m^3 |
| g/cm^3 | gramo por centimetro cubico | 10^{3} kg/m^3 |
ID:(198, 0)
Modelo
Top 
Parámetros
Variables
Cálculos
Cálculos
Cálculos
Ecuaciones
m_a = \rho_a v_a
m_a = rho_a * v_a
m_c = \rho_c v_c
m_c = rho_c * v_c
m_i = \rho_i v_i
m_i = rho_i * v_i
v_a =\displaystyle\frac{4 \pi }{3} r_a ^3
v_a = 4* pi * r_a ^3/3
v_c = w_c l_c ^2
v_c = w_c * l_c ^2
v_i = a_i ^3
v_i = a_i ^3
ID:(15215, 0)
Volumen de un grano de arena
Ecuación 
Si modelamos un grano de arena como una esfera y asumimos que el radio del grano de arena (r_a), podemos calcular su el volumen de un grano de arena (v_a) utilizando la siguiente ecuación:
Sin embargo, es importante tener en cuenta que este cálculo proporciona un valor estimado del volumen, ya que el radio es un valor promedio. Para obtener un cálculo más preciso e incluso determinar un volumen promedio, sería necesario estudiar la distribución de los radios de los granos de arena en el estudio.
Es relevante destacar que el volumen calculado es solo un valor de referencia, ya que se basa en la suposición de que la arena está compuesta por esferas perfectas e idénticas, lo cual no es el caso en la realidad.
ID:(4238, 0)
Volumen de un grano de limo
Ecuación 
Si modelamos un grano de limo como un paralelepipedo recto y asumimos que el lado del grano de limo (a_i), podemos calcular su el volumen de un grano de limo (v_i) utilizando la siguiente ecuación:
Sin embargo, es importante destacar que este cálculo proporciona un valor estimado del volumen, ya que el lado es un valor promedio. Para obtener un cálculo más preciso e incluso determinar un volumen promedio, sería necesario estudiar la distribución de los lados de los granos de limo en el estudio.
Es relevante enfatizar que el volumen calculado sirve como un valor de referencia, ya que se basa en la suposición de que el limo está compuesto por cubos perfectas e idénticas, lo cual no es el caso en la realidad.
ID:(15060, 0)
Volumen de una plaquita de arcilla
Ecuación 
Si modelamos un grano de arcilla como un paralelepípedo recto y asumimos que tiene el largo y ancho de una plaquita de arcilla (l_c) y la altura de una plaquita de arcilla (w_c), podemos calcular el volumen de un grano de arcilla (v_c) mediante:
Sin embargo, es importante tener en cuenta que este cálculo proporciona un valor estimado del volumen, ya que los lados y la altura son valores promedio. Para obtener un cálculo más preciso e incluso determinar un volumen promedio, sería necesario estudiar la distribución de los lados y alturas de los granos de arcilla en el estudio.
Es relevante destacar que el volumen calculado es solo un valor de referencia, ya que se basa en la suposición de que la arcilla está compuesta por paralelepipedos rectos perfectas e idénticas, lo cual no es el caso en la realidad.
ID:(4239, 0)
Masa de un grano de arena
Ecuación 
Una vez que disponemos de el volumen de un grano de arena (v_a) y la densidad de un grano de arena (\rho_a), podemos determinar la masa de un grano de arena (m_a) mediante la siguiente ecuación:
Sin embargo, es importante tener en cuenta que tanto el volumen como la densidad del grano de arena son estimaciones, por lo que la masa resultante es principalmente un valor de referencia. Para realizar un cálculo más preciso, sería necesario analizar la distribución de las formas y composiciones mineralógicas para obtener un valor medio más exacto.
Es fundamental destacar que la masa calculada se utiliza como punto de referencia, ya que se basa en la suposición de que la arena está compuesta por esferas perfectas y que las densidades de los granos son idénticas, lo cual no es el caso en la realidad.
ID:(15061, 0)
Masa de un grano de limo
Ecuación 
Una vez que disponemos de el volumen de un grano de limo (v_i) y la densidad de un grano de limo (\rho_i), podemos determinar la masa de un grano de limo (m_i) mediante la siguiente ecuación:
Sin embargo, es fundamental recordar que tanto el volumen como la densidad del grano de limo son estimaciones, por lo que la masa resultante es un valor de referencia. Para obtener un cálculo más preciso, sería necesario estudiar la distribución de las formas y composiciones mineralógicas para obtener un valor medio más exacto.
Es relevante subrayar que la masa calculada sirve como un punto de referencia, ya que se basa en la suposición de que el limo está compuesto por esferas perfectas y que las densidades de los granos son idénticas, lo cual no es el caso en la realidad.
ID:(15062, 0)
Masa de un grano de arcilla
Ecuación 
Una vez que disponemos de el volumen de un grano de arcilla (v_c) y la densidad de un grano de arcilla (\rho_c), podemos determinar la masa de una plaquita de arcilla (m_c) mediante la siguiente ecuación:
Sin embargo, es fundamental recordar que tanto el volumen como la densidad del grano de arcilla son estimaciones, por lo que la masa resultante es un valor de referencia. Para obtener un cálculo más preciso, sería necesario estudiar la distribución de las formas y composiciones mineralógicas para obtener un valor medio más exacto.
Es relevante subrayar que la masa calculada sirve como un punto de referencia, ya que se basa en la suposición de que la arcilla está compuesta por paralelepípedos perfectos y que las densidades de los granos son idénticas, lo cual no es el caso en la realidad.
ID:(15063, 0)
