Bodenbestandteile
Storyboard 
Die drei Hauptkomponenten des Bodens sind Sand, Schluff und Ton. Während Sand- und Schluffkörner relativ kugelförmig sind, ähneln Tonpartikel kleinen Flächen oder Plättchen. Es besteht auch ein erheblicher Unterschied in ihren Größen: Sandkörner sind nur ein Bruchteil eines Millimeters groß, Schluffkörner haben Abmessungen im Bereich von Mikrometern, und Tonpartikel sind noch kleiner und messen nur wenige Mikrometer.
Diese Variation in den Partikelgrößen hat einen signifikanten Einfluss auf die Fähigkeit des Bodens zur Verdichtung. Zum Beispiel kann Ton die Zwischenräume zwischen Sand- und Schluffkörnern ausfüllen, was die verschiedenen Grade der Verdichtung beeinflusst, die im Boden erreicht werden können.
ID:(362, 0)
Oberflächenboden
Konzept 
Wenn wir die Oberfläche des Bodens betrachten, sehen wir oft einige Steine oder Felsen, eine braune Masse, die wir als Boden bezeichnen, und einige Pflanzen.

Acker im Gewann Bising beim Dorf Oberwilzingen, Schwäbische Alb durch Ustill (commons.wikimedia.org).
Bei genauerer Betrachtung werden wir jedoch feststellen, dass der Boden Pflanzenreste enthält, von kleineren Steinen bis zu Sandkörnern. Diese zersetzten Pflanzenreste stellen organisches Material von kleinerer Größe dar, das sich manchmal mit dem Bodenmaterial vermischt.
Zusammenfassend können wir identifizieren:
• Felsbrocken, Kieselsteine und kleine Steine.
• Organische Materie im Boden.
• Den Boden selbst.
ID:(15075, 0)
Felsbrocken, Kieselsteine, Kiesel
Konzept 
In allen Arten von Boden finden wir Felsbrocken, Kieselsteine und kleine Steine, die in verschiedenen Tiefen verteilt sind. Ebenso bleiben diese Steine, wenn die Oberfläche des Bodens erodiert, oft auf der Oberfläche liegen, da der umgebende Boden durch oberflächliche Wasserströme weggespült wurde.

Kieselsteine an einem Strand in Broulee, Australien von Steve Shattuck (commons.wikimedia.org)
Die Konzentration von Felsbrocken, Kieselsteinen und kleinen Steinen variiert und beeinflusst die mechanischen und hydrodynamischen Eigenschaften des Bodens. Einerseits stabilisieren die Steine im Bodeninneren den Boden und verleihen ihm eine größere Widerstandsfähigkeit gegen Deformation. Andererseits hindern sie aufgrund ihrer fehlenden Porosität den Wasserfluss und beeinträchtigen sowohl den Wasserfluss als auch den Feuchtigkeitstransport durch Diffusion. In dieser Hinsicht sollte die Rolle der Steine bei der Bodenmodellierung berücksichtigt werden.
ID:(15077, 0)
Organisches Material
Konzept 
In den Poren des oberflächlichen Bodens findet sich organische Materie, zu der Pflanzen- und Tierreste, mikrobielle Biomasse, Humus und von den Wurzeln abgegebene Substanzen gehören.

Do-It-Yourself-Leitfaden für die Mikroskopie landwirtschaftlicher Böden, Katelyn Solbakk, Mikroliv, Okologisk Landsforening
Innerhalb der mikrobiellen Biomasse finden wir Mikroorganismen wie Bakterien und Pilze. Humus hingegen ist hoch zersetztes organisches Material, das aus pflanzlichen und mikrobiellen Quellen stammt. Es verbessert signifikant die Fähigkeit des Bodens, Nährstoffe und Wasser zu speichern.
ID:(15078, 0)
Boden in der Tiefe
Konzept 
Wenn wir einen Querschnitt des Bodens betrachten, sehen wir die Pflanzenbedeckung an der Oberfläche, und darunter die Wurzeln, die die obersten Zentimeter des Bodens durchdringen, der organische Materie enthält. Unter organischer Materie verstehen wir verrottendes Material, Organismen und Mikroorganismen, die in wässrigen Umgebungen gedeihen, weshalb sie die Bodenporen bewohnen, in denen Wasser vorhanden ist.

Bodenbearbeitung in Palos Verdes, Chaihuin, Chile von W.Gerber
Wenn wir weiter nach unten schauen, bemerken wir, dass die organische Materie allmählich verschwindet und den darunter liegenden Boden freilegt, der aus seinen drei Komponenten Sand, Schluff und Ton sowie Gesteinen besteht. Die Konzentration dieser verschiedenen Komponenten variiert und erzeugt unterschiedliche Schichten mit verschiedenen physikalischen Eigenschaften und unterschiedlicher Fähigkeit zur Aufnahme und zum Transport von Wasser.
Zusammenfassend können wir im Boden Komponenten identifizieren, die sich von der organischen Materie und den Hauptgesteinen unterscheiden:
• Sand
• Schluff
• Ton
ID:(15076, 0)
Sand
Konzept 
Feinsand ist ein Typ von Bodenpartikeln, der sich durch seine relativ kleine Größe auszeichnet. Er liegt in der Größe zwischen groberen Sandpartikeln und feineren Schluffpartikeln. Die Partikel von Feinsand haben in der Regel eine Größe von 0,02 bis 0,2 Millimetern oder 20 bis 200 Mikrometern.
Feinsand kommt häufig in Bodenzusammensetzungen vor und zeichnet sich durch seine Fähigkeit aus, eine bestimmte Menge Feuchtigkeit zu speichern, während er gleichzeitig für angemessene Drainage sorgt. Er kann zur Bodentextur beitragen und die Fähigkeit des Bodens zur Unterstützung des Pflanzenwachstums beeinflussen. Böden mit einem höheren Anteil an Feinsand neigen dazu, gute Belüftungs- und Drainageeigenschaften zu haben.

Dünen von Erg Awbari (Idehan Ubari) in der Sahara-Wüstenregion des Distrikts Wadi Al Hayaa in der Region Fezzan im Südwesten Libyens, aufgenommen von Luca Galuzzi (commons.wikimedia.org).
Die chemische Zusammensetzung von Sand kann je nach Herkunft und Mineralzusammensetzung variieren. Sand besteht im Allgemeinen aus verschiedenen Mineralien, wobei Quarz eines der häufigsten ist. Die genaue chemische Zusammensetzung von Sand kann jedoch stark variieren. Hier ist eine allgemeine Übersicht über die chemische Zusammensetzung von Sand mit ungefähren Prozentbereichen:
• Quarz (SiO_2) 90% - 95% [1]: Siliciumdioxid, allgemein als Silika bekannt, ist die Hauptkomponente der meisten Sande. Es kann zwischen 60% und 95% oder mehr der Zusammensetzung des Sands ausmachen.
• Feldspat (KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8) <10% [1]: Feldspat ist ein weiteres häufiges Mineral im Sand, und seine Zusammensetzung kann variieren. Kaliumfeldspat (K-Feldspat), Natriumfeldspat (Na-Feldspat) und Kalziumfeldspat (Ca-Feldspat) sind verschiedene Arten von Feldspatmineralien, die im Sand vorkommen.
• Glimmer (Muskovit, Biotit) 1-5% [1]: Glimmermineralien wie Muskovit und Biotit können zwischen 1% und 5% oder weniger der Siltzusammensetzung ausmachen.
• Andere Mineralien: Abhängig von der geologischen Herkunft des Sands können Spuren anderer Mineralien wie Feldspat, Glimmer oder Magnetit enthalten sein.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2080, 0)
Schluff
Konzept 
Silt ist eine Art von Bodenpartikel, die in Bezug auf die Partikelgröße zwischen Sand und Ton liegt. Silt-Partikel haben in der Regel eine Größe zwischen 0,002 und 0,02 Millimetern, was 2 bis 20 Mikrometern entspricht. Diese Partikel sind kleiner als Sand, aber größer als Ton.
Ein charakteristisches Merkmal von Silt ist seine Fähigkeit, Feuchtigkeit und Nährstoffe zu speichern, was es für die Landwirtschaft geeignet macht. Es ist jedoch wichtig zu beachten, dass Silt sich verdichten und Entwässerungsprobleme verursachen kann, wenn es die Bodenzusammensetzung dominiert. Böden mit Siltgehalt sind oft fruchtbar und können eine Vielzahl von Kulturen unterstützen, wenn sie ordnungsgemäß bewirtschaftet werden.
Die chemische Zusammensetzung von Silt kann je nach Herkunft und geografischem Standort variieren. In allgemeinen Begriffen besteht Silt jedoch aus verschiedenen Mineralien und kann organische Materie enthalten. Im Folgenden gebe ich eine Annäherung an die chemische Zusammensetzung von Silt in Bezug auf die Hauptelemente an, ausgedrückt als Prozentsatz der Gesamtzusammensetzung:
• Quarz (SiO_2) 40-60% [1]: Quarz ist oft das dominierende Mineral im Silt und macht in der Regel etwa 50% bis 70% oder sogar mehr seiner Zusammensetzung aus.
• Feldspat (KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8) <10% [1]: Feldspatmineralien, einschließlich Kalifeldspat, Natriumfeldspat und Kalziumfeldspat, können etwa 10% bis 30% oder mehr der Zusammensetzung ausmachen.
• Glimmer (Muskovit, Biotit) < 5% [1]: Glimmermineralien wie Muskovit und Biotit können zwischen 1% und 5% oder weniger der Siltzusammensetzung ausmachen.
• Andere Mineralien: Silt kann Spuren verschiedener anderer Mineralien je nach seiner spezifischen geologischen Herkunft enthalten, wie Zirkon, Granat und andere.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2068, 0)
Ton
Konzept 
Ton ist ein Typ von Bodenpartikel mit sehr feinen Partikeln, typischerweise kleiner als 0,002 Millimeter oder weniger als 2 Mikrometer. Tonpartikel sind deutlich kleiner als Sand- und Schluffpartikel. Tonböden sind für ihre Fähigkeit bekannt, Wasser und Nährstoffe aufgrund ihrer geringen Partikelgröße und großen Oberfläche zu speichern. Allerdings können sie sich auch leicht verdichten und möglicherweise eine schlechte Entwässerung aufweisen. Tonböden können je nach ihrer mineralischen Zusammensetzung und dem Gehalt an organischem Material in Farbe und Textur variieren. Sie sind eine wichtige Komponente vieler Bodentypen und können die Bodenfruchtbarkeit und -struktur beeinflussen.

Quartäre Tonablagerungen in Estland (400.000 Jahre alt) von Siim Sepp (commons.wikimedia.org)
Die chemische Zusammensetzung von Ton kann je nach spezifischer mineralischer Zusammensetzung und Herkunft variieren. Ton besteht hauptsächlich aus winzigen mineralischen Partikeln und setzt sich in der Regel aus verschiedenen Mineralien zusammen, darunter:
• Kaolinit (Al_2Si_2O_5(OH)_4) 20-40% [1]: Kaolinit ist ein häufiges Tonmineral und der Hauptbestandteil von Kaolinton.
• Illit ((K, H_3O)(Al, Mg, Fe)_2(Si, Al)_4O_{10}[(OH)_2,(H_2O)]) 10-40% [1]: Illit ist ein weiteres häufiges Tonmineral.
• Smektit/Montmorillonit ((Na, Ca)_{0.33}(Al, Mg)_2(Si_4O_{10})(OH)_2·n(H_2O)) 10-40% [1]: Montmorillonit ist ein Tonmineral, das für seine Quelleigenschaften bekannt ist.
• Chlorit ((Mg, Fe)_3(Si, Al)_4O_{10}(OH)_2·(Mg, Fe)_3(OH)_6) <10% [1]: Chlorit wird manchmal in Tonmineralien gefunden.
• Andere Minerale: Je nach spezifischer Tonablagerung können auch andere Minerale in geringen Mengen vorhanden sein, einschließlich Quarz, Feldspat und verschiedenen Metalloxiden.
[1] Clay Mineralogy, Ralph E. Grim, McGraw-Hill International Series
ID:(2069, 0)
Kornform
Konzept 
Um den Boden effektiv zu modellieren, ist es entscheidend, die geometrischen Formen zu berücksichtigen, die am besten die verschiedenen Arten von Körnern beschreiben, die den Boden ausmachen.
Dazu ist es erforderlich, mehrere Körner jeder Art zu beobachten. Im Falle von Sand ist dies mit einem herkömmlichen Mikroskop möglich und ermöglicht die Sammlung von Körnern, wie sie im folgenden Bild gezeigt werden:

Sandkörner aus gelbem Bausand. Mikroskop Lumam R-8. EPI-Beleuchtung. Das Foto jedes Sandkorns ist das Ergebnis einer multifokalen Stapelung von Alexander Klepnev (commons.wikimedia.org).
In diesem Fall können wir schlussfolgern, dass die Form abgerundet ist, was es uns ermöglicht, sie effektiv als Kugeln darzustellen.
ID:(2257, 0)
Bildung von Sand- und Schluffkörnern
Konzept 
In der Regel bestehen Sandkörner und Schluffkörner aus Konglomeraten mehrerer Kristalle, die Stößen ausgesetzt sind, während sie von Wasser oder Wind transportiert werden. Diese Stöße erzeugen Brüche entlang der Kristallflächen, entfernen herausragende Fragmente und runden so das Korn ab:
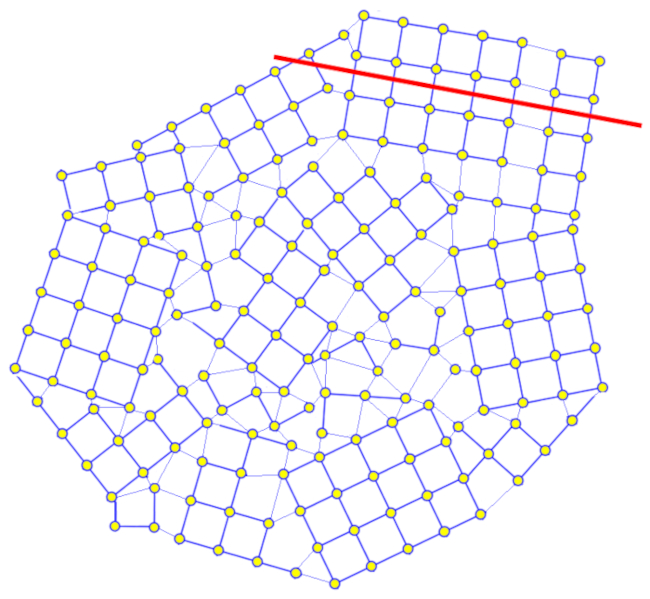
Das Korn wird abgerundet, während seine Ecken allmählich abnutzen.
Auf diese Weise neigen sie dazu, sich abzurunden und eine Form anzunehmen, die kleinen Kugeln ähnelt.
ID:(2081, 0)
Bildung von Tonkörnern
Konzept 
Tonkörner sind in der Regel kleine Kristalle, die Stößen ausgesetzt sind, während sie von Wasser oder Wind transportiert werden. Diese Stöße erzeugen Brüche entlang der Kristallebenen, was bedeutet, dass der Korn seine Form beibehält, ohne die Ecken abzurunden:
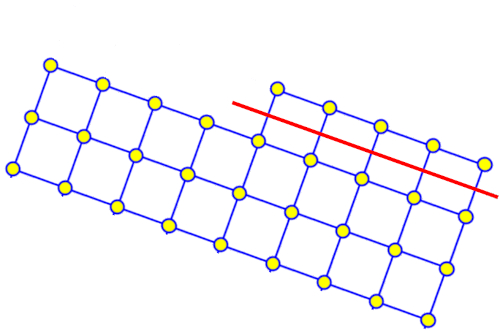
Das Korn behält seine Form, da es dazu neigt, sich allmählich entlang der gleichen Ebene abzunutzen, die seine Form definiert.
Daher zeichnen sich Tonkörner durch eine geometrische Form aus, die kleinen Platten ähnelt und geraden Quader ähnelt.
ID:(2083, 0)
Form von Sandkörnern
Konzept 
Wenn wir die Körner unter einem Mikroskop betrachten, werden wir feststellen, dass sie relativ runde Formen und variable Größen haben, obwohl sie tendenziell eine ähnliche Größe haben:

Körner des sogenannten 'Ottawa Silica Sand' unter einem Elektronenmikroskop. Vergrößerung 150x. Der 'Ottawa Sand' ist ein Nebenprodukt des hydraulischen Bergbaus von Ordovizischen Orthokvartzen aus der St. Peter Sandsteinformation des paläozoischen intrakratonischen Illinois-Beckens durch die NASA (commons.wikimedia.org).
Daher können die Körner in einer ersten Annäherung als Kugeln modelliert werden:
Sandkörner können als Kugeln modelliert werden. Um das Modell zu vereinfachen, wird angenommen, dass sie alle identisch sind. Ein detaillierteres Modell könnte jedoch die Verteilung verschiedener Radien berücksichtigen.
In Übereinstimmung mit der anfänglichen Hypothese, dass Sandkörner als Kugeln modelliert werden können, kann ihr entsprechender Radius eingeführt werden.
Daher führen wir den Radius der Volumen eines Schlickkorns (r_a) ein, um die Kugeln der Sandkörner zu beschreiben.
Es sollte beachtet werden, dass der Radius ein Durchschnittswert ist, da er zwischen verschiedenen Körnern variiert.
ID:(15054, 0)
Schleimkornform
Konzept 
Wenn wir die Schluffkörner unter einem Mikroskop betrachten, werden wir feststellen, dass sie relativ kubische Formen und unterschiedliche Größen haben, obwohl sie tendenziell eine ähnliche Größe aufweisen:

Initial silt Proctor compaction at optimum wtare content - high magnification, Scanning Electron Microscope (SEM) investigations in soil microstructure description, Dimitri Deneele, 1st IMEKO TC-4 International Workshop on Metrology for Geotechnics, Benevento, Italy, March 17-18, 2016
Daher können die Körner als erste Annäherung als Würfel modelliert werden:
Die Schluffkörner können als Würfel modelliert werden. Um das Modell zu vereinfachen, wird angenommen, dass sie alle die gleiche Größe haben. Ein detaillierteres Modell könnte jedoch die Verteilung unterschiedlicher Seitenlängen berücksichtigen.
Im Einklang mit der anfänglichen Annahme, dass Schluffkörner als Würfel modelliert werden können, kann ihre entsprechende Seitenlänge eingeführt werden.
Daher führen wir die Würfelseite der Schlickkornseite (a_i) ein, um die Körner von Schluff zu beschreiben.
Es sollte beachtet werden, dass die Seitenlänge einen Durchschnittswert darstellt, da sie bei verschiedenen Körnern variieren kann.
ID:(15056, 0)
Tonkornform
Konzept 
Tonkörner sind relativ flach und neigen dazu, sich parallel zu stapeln, wie auf diesem Bild zu sehen ist, das mit einem Elektronenmikroskop aufgenommen wurde:

SEM image of well crystallized crystallizedkaolinite from sandstone. Note hexagonal morphology,smooth basal surfaces and abundance of slit- andwedge-shaped pores. (The influence of individual clay minerals on formation damage of reservoir sandstones: A critical review with some new insights, Jeff Wilson, L. Wilson, Ian T.M. Patey, May 2014Clay Minerals 49(2))
Ihre Form ähnelt flachen Elementen mit reduzierter Dicke, die rechteckigen Parallelepipeden ähneln:
Tonkörner können als rechteckige Parallelepipeden modelliert werden. Zur Vereinfachung des Modells wird angenommen, dass sie alle identisch sind. Ein detaillierteres Modell könnte jedoch die Verteilung verschiedener Längen und Höhen berücksichtigen.
Im Einklang mit der anfänglichen Hypothese, dass Tonkörner als rechteckige Parallelepipeden modelliert werden können, können ihre entsprechenden Längen und Höhen eingeführt werden.
Daher wird es eingeführt, um das rechtwinklige Parallelepipedon der Länge und Breite eines Tonplättchens (l_c) und die Höhe eines Tonplättchens (w_c) zu beschreiben.
Es sollte beachtet werden, dass die Längen und die Höhe Durchschnittswerte sind, da sie tatsächlich zwischen verschiedenen Körnern variieren.
ID:(15055, 0)
Sandkorndichte
Variable 
Um die Masse eines Sandkorns zu berechnen, ist es notwendig, seine Dichte zu kennen. Es ist jedoch wichtig zu beachten, dass die Dichte des einzelnen Korns aufgrund seiner hohen Porosität erheblich von der Gesamtdichte des Sandes abweicht. Daher müssen wir zur Schätzung der Dichte eines Sandkorns die Dichte seiner Hauptminerale untersuchen, wie unten aufgeführt:
| Mineral | Vorkommen && Dichte [g/cm^3] | |
| Quarz | 90-95% [1] | 2,65 [2] |
| Feldspäte | <10% [1] | 2,50-2,80 [2] |
| Glimmer | <5% [1] | 2,70-3,30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Um ein einfaches Modell zu entwickeln, können wir von einer homogenen Dichte ausgehen:
Wenn wir annehmen, dass die Minerale, aus denen die Sandkörner bestehen, gleichmäßig verteilt sind, können wir davon ausgehen, dass die Körner eine konstante und einheitliche Dichte in allen von ihnen haben.
Dadurch wird die Dichte eines Sandkorns (\rho_a) eingeführt.
Es ist wichtig zu beachten, dass dieser Wert je nach der spezifischen Zusammensetzung der Sandkörner variieren kann.
ID:(15057, 0)
Dichte eines Schluffkorns
Variable 
Um die Masse eines Schluffkorns zu berechnen, ist es unerlässlich, seine Dichte zu kennen. Es ist jedoch wichtig zu betonen, dass die Dichte des einzelnen Korns signifikant von der Dichte des Schlamms als Ganzes abweicht, aufgrund der erheblichen Porosität in letzterem. Daher ist es notwendig, um die Dichte eines Schluffkorns abzuschätzen, die Dichte seiner Hauptminerale zu analysieren, die nachstehend detailliert aufgeführt sind:
| Mineral | Vorkommen && Dichte [g/cm^3] | |
| Quarz | 40-60% [1] | 2,65 [2] |
| Feldspäte | <10% [1] | 2,50-2,80 [2] |
| Glimmer | <5% [1] | 2,70-3,30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Um ein einfaches Modell zu entwickeln, können wir von einer homogenen Dichte ausgehen:
Wenn wir annehmen, dass die Minerale, aus denen die Schlickkörner bestehen, gleichmäßig verteilt sind, können wir davon ausgehen, dass die Körner eine konstante und einheitliche Dichte in allen von ihnen haben.
Dadurch wird die Dichte eines Schluffkorns (\rho_i) eingeführt.
Es ist wichtig zu beachten, dass dieser Wert je nach der Zusammensetzung der Schluffkörner variieren kann.
ID:(15059, 0)
Dichte eines Tonkorns
Variable 
Um die Masse eines Tonkorns zu berechnen, ist es entscheidend, seine Dichte zu kennen. Es ist jedoch wichtig zu betonen, dass die Dichte des einzelnen Korns signifikant von der Dichte des Tons als Ganzes abweicht, aufgrund der erheblichen Porosität in letzterem. Daher ist es notwendig, um die Dichte eines Tonkorns abzuschätzen, die Dichte seiner Hauptminerale zu analysieren, die nachstehend detailliert aufgeführt sind:
| Mineral | Vorkommen && Dichte [g/cm^3] | |
| Smektit | 0-80% [1] | 2.75-2.78 [2] |
| Illit | 10-80% [1] | 2.60-2.86 [2] |
| Kaolinit | 20-80% [1] | 2.62-2.66 [2] |
| Chlorit | 0-30% [1] | 2.60-2.96 [2] |
[1] Clay Mineralogy, Ralph E. Grim (1968), McGraw-Hill
[2] Geotechnical Engineering Principles and Practices, Donald P. Coduto et al. (1998), Prentice-Hall
Um ein einfaches Modell zu entwickeln, können wir von einer homogenen Dichte ausgehen:
Wenn wir annehmen, dass die Minerale, aus denen die Tonkörner bestehen, gleichmäßig verteilt sind, können wir davon ausgehen, dass die Körner eine konstante und einheitliche Dichte in allen von ihnen haben.
Dadurch wird die Dichte eines Tonkorns (\rho_c) eingeführt.
Es ist wichtig zu beachten, dass dieser Wert je nach der spezifischen Zusammensetzung der Tonkörner variieren kann.
ID:(15058, 0)
USGS-Diagramm mit Getreidemessungen
Bild 
Die Untersuchung der Körner in einer Bodenprobe umfasst eine umfassende Analyse verschiedener Aspekte, die zur Erklärung der physikalischen Eigenschaften und des Verhaltens des Bodens beitragen. Hier ist eine ausführlichere Erklärung der wichtigsten Komponenten dieser Studie:
Größenbegriffe:
- Größenbegriffe beziehen sich auf die Kategorisierung von Bodenpartikeln nach ihrem Durchmesser. Bodenpartikel werden in der Regel in drei Hauptkategorien unterteilt:
Sand: Die größten Partikel mit Durchmessern von 0,05 mm bis 2 mm.
Schluff: Mittelgroße Partikel im Bereich von 0,002 mm bis 0,05 mm.
Ton: Die kleinsten Partikel mit Durchmessern von weniger als 0,002 mm.
- Die relativen Anteile dieser Größenfraktionen bestimmen die Bodentextur, die wiederum Eigenschaften wie Wasserrückhaltung und Drainage beeinflusst.
Siebgrößen:
- Siebgrößen sind standardisierte Maschengrößen, die zur Trennung von Bodenpartikeln nach Größe verwendet werden. Gemeinsame Siebgrößen werden durch die ASTM (American Society for Testing and Materials) oder ISO (International Organization for Standardization) Standards definiert.
- Die Siebanalyse beinhaltet das Passieren einer Bodenprobe durch einen Satz von Sieben mit progressiv feineren Maschengrößen, um die Partikelgrößenverteilung zu bestimmen.
Anzahl der Körner pro mg:
- Diese Metrik repräsentiert die Dichte von Bodenpartikeln innerhalb einer gegebenen Masse Boden. Sie wird berechnet, indem die Anzahl der Partikel in einer bekannten Masse Boden (in der Regel 1 mg) gezählt und dann extrapoliert wird, um die Gesamtzahl der Partikel in einer größeren Probe zu schätzen.
- Sie liefert Einblicke in die Bevölkerung und den Abstand von Bodenpartikeln, was für das Verständnis von Bodenverdichtung und Wurzeldurchdringung wichtig sein kann.
Setzgeschwindigkeit:
- Die Setzgeschwindigkeit bezieht sich auf die Geschwindigkeit, mit der Bodenpartikel unter dem Einfluss der Schwerkraft durch ein Fluid (normalerweise Wasser) fallen. Sie wird durch die Größe, Form und Dichte der Partikel sowie die Viskosität des Fluids bestimmt.
- Das Wissen über Setzgeschwindigkeiten ist in Sedimentationsstudien wertvoll und kann dazu beitragen, vorherzusagen, wie lange es dauert, bis sich Partikel aus der Suspension in Gewässern absetzen.
Schwellengeschwindigkeit für die Traktion:
- Die Schwellengeschwindigkeit für die Traktion repräsentiert die minimale Geschwindigkeit des Wasserflusses, die erforderlich ist, um die Bewegung von Bodenpartikeln auf dem Bett eines Flusses oder Baches zu initiieren. Sie ist ein wichtiger Parameter in Sedimenttransportstudien.
- Wenn die Wasserströmungsgeschwindigkeit die Schwellengeschwindigkeit für eine bestimmte Partikelgröße überschreitet, kann sie diese Partikel erodieren und transportieren, was erhebliche Umweltauswirkungen haben kann.
Als Beispiel hier die Tabelle der Partikelgrößen, die vom United States Geological Survey (USGS) im Long Island Sound gemessen wurden.
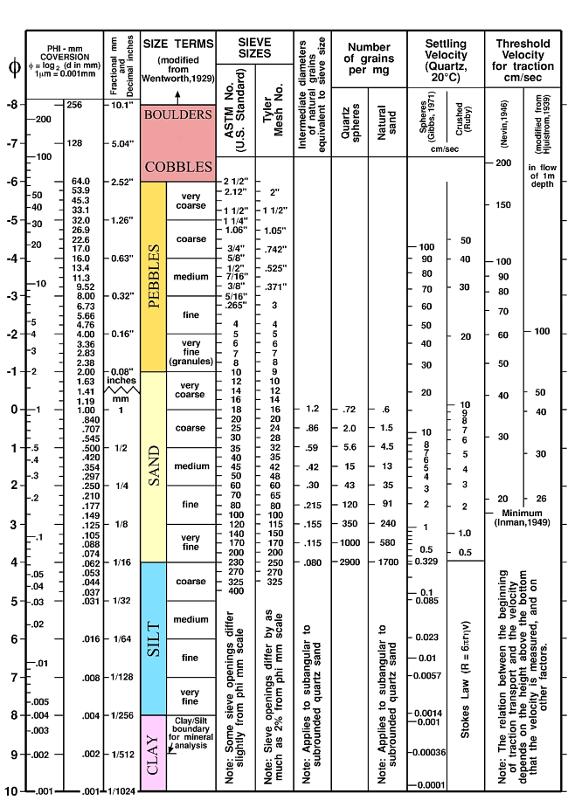
usgs-ofr-00-304
ID:(6941, 0)
Modellparameter
Beschreibung 
Das Modell kann definiert werden, basierend auf der Existenz von drei Arten von Materialien (Sand, Schluff und Ton), wobei die Körner wie folgt modelliert werden: In den ersten beiden Fällen werden die Körner als Kugeln mit unterschiedlichen durchschnittlichen Radien dargestellt, und im Fall von Ton werden die Körner als gerade Quader modelliert.
Die Parameterbereiche sind in der folgenden Tabelle zusammengefasst:
| Typ | Parameter | Symbol | Bereich | Einheit |
| Arena | Radio | r_a | 62 - 2000 | \mu m |
| Volumen | v_a | 1 - 33500 | nl | |
| Dichte | \rho_a | 2,64 - 2,69 | g/cm^3 | |
| Masse | m_a | 2,6 - 90100 | \mu g | |
| Schleim | Radius | r_i | 4 - 62 | \mu m |
| Volumen | v_i | 0,27 - 990 | pl | |
| Dichte | \rho_i | 2,63 - 2,72 | g/cm^3 | |
| Masse | m_i | 0,71 - 2700 | ng | |
| Ton | Länge | l_c | 1 - 4 | \mu m |
| Höhe | w_c | 0,1 - 0,4 | \mu m | |
| Volumen | v_c | 0,1 - 6,4 | fl | |
| Dichte | \rho_c | 2,66 - 2,80 | g/cm^3 | |
| Masse | m_c | 0,27 - 17,9 | pg |
Da die Körner so klein sind, ist es notwendig, in einem großen Größenbereich zu arbeiten. Aus diesem Grund werden Abkürzungen verwendet:
Lang
| Symbol | Einheit | MKS |
| m | Meter | 1 m |
| mm | Millimeter | 10^{-3} m |
| \mu m | Mikrometer | 10^{-6} m |
Volumen
| Symbol | Einheit | MKS |
| m^3 | Kubikmeter | 1 m^3 |
| l | Liter | 10^{-3} m^3 |
| ml | Milliliter | 10^{-6} m^3 |
| \mu l | Mikroliter | 10^{-9} m^3 |
| nl | Nanoliter | 10^{-12} m^3 |
| pl | Pikoliter | 10^{-15} m^3 |
| fl | Fentoliter | 10^{-18} m^3 |
Masse
| Symbol | Einheit | MKS |
| kg | Kilogramm | 1 kg |
| g | Gramm | 10^{-3} kg |
| mg | Milligramm | 10^{-6} kg |
| \mu g | Mikrogramm | 10^{-9} kg |
| ng | Nanogramm | 10^{-12} kg |
| pg | Pikogramm | 10^{-15} kg |
Dichte
| Symbol | Einheit | MKS |
| kg/m^3 | Kilogramm pro Kubikmeter | 1 kg/m^3 |
| g/cm^3 | Gramm pro Kubikzentimeter | 10^{3} kg/m^3 |
ID:(198, 0)
Modell
Top 
Parameter
Variablen
Berechnungen
Berechnungen
Berechnungen
Gleichungen
m_a = \rho_a v_a
m_a = rho_a * v_a
m_c = \rho_c v_c
m_c = rho_c * v_c
m_i = \rho_i v_i
m_i = rho_i * v_i
v_a =\displaystyle\frac{4 \pi }{3} r_a ^3
v_a = 4* pi * r_a ^3/3
v_c = w_c l_c ^2
v_c = w_c * l_c ^2
v_i = a_i ^3
v_i = a_i ^3
ID:(15215, 0)
Volumens eines Sandkorns
Gleichung 
Wenn wir ein Sandkorn als Kugel modellieren und davon ausgehen, dass der Volumen eines Schlickkorns (r_a) ist, können wir seinen der Volumen eines Sandkorns (v_a) mit der folgenden Gleichung berechnen:
Diese Berechnung liefert ein geschätztes Volumen, da der Radius einen Durchschnittswert darstellt. Um eine genauere Berechnung zu erhalten oder sogar ein durchschnittliches Volumen zu bestimmen, wäre es notwendig, die Verteilung der Radien der Sandkörner in der Studie zu untersuchen.
Es ist wichtig zu beachten, dass das berechnete Volumen lediglich ein Referenzwert ist, da es auf der Annahme basiert, dass der Sand aus perfekten und identischen Kugeln besteht, was in der Realität nicht der Fall ist.
ID:(4238, 0)
Volumen eines Schlickkorns
Gleichung 
Wenn wir ein Korn Schluff als rechtwinkliges Parallelepiped modellieren und annehmen, dass der Schlickkornseite (a_i) ist, können wir es der Volumen eines Schlickkorns (v_i) mit folgender Gleichung berechnen:
Es ist jedoch wichtig zu beachten, dass diese Berechnung einen geschätzten Wert des Volumens liefert, da die Seitenlänge einen Durchschnittswert darstellt. Um eine genauere Berechnung zu erhalten und sogar ein durchschnittliches Volumen zu bestimmen, wäre es notwendig, die Verteilung der Seitenlängen der Schluffkörner in der Studie zu untersuchen.
Es ist wichtig zu betonen, dass das berechnete Volumen als Referenzwert dient, da es auf der Annahme basiert, dass Schluff aus perfekten und identischen Würfeln besteht, was in der Realität nicht der Fall ist.
ID:(15060, 0)
Volumens eines Tonplättchen
Gleichung 
Wenn wir ein Tonkorn als rechtwinkliges Parallelepiped modellieren und annehmen, dass es die Maße der Länge und Breite eines Tonplättchens (l_c) und die Höhe eines Tonplättchens (w_c) hat, können wir der Volumen eines Tonkorns (v_c) mithilfe der folgenden Gleichung berechnen:
Es ist jedoch wichtig zu beachten, dass diese Berechnung einen geschätzten Volumenwert liefert, da die Längen und die Höhe Durchschnittswerte sind. Um eine genauere Berechnung durchzuführen und sogar ein durchschnittliches Volumen zu bestimmen, wäre es notwendig, die Verteilung der Längen und Höhen der Tonkörner in der Studie zu untersuchen.
Es ist hervorzuheben, dass das berechnete Volumen als Referenzwert dient, da es auf der Annahme basiert, dass der Ton aus perfekten und identischen rechten rechteckigen Quadern besteht, was in der Realität möglicherweise nicht der Fall ist.
ID:(4239, 0)
Masse eines Sandkorns
Gleichung 
Sobald wir der Volumen eines Sandkorns (v_a) und die Dichte eines Sandkorns (\rho_a) haben, können wir die Masse eines Sandkorns (m_a) durch Verwendung der folgenden Gleichung berechnen:
Es ist jedoch wichtig zu bedenken, dass sowohl das Volumen als auch die Dichte des Sandkorns Schätzungen sind, wodurch die resultierende Masse hauptsächlich ein Referenzwert ist. Für eine genauere Berechnung wäre es erforderlich, die Verteilung der Formen und mineralogischen Zusammensetzungen zu untersuchen, um einen genauer durchschnittlichen Wert zu erhalten.
Es ist relevant zu betonen, dass die berechnete Masse als Referenzpunkt dient, da sie auf der Annahme basiert, dass der Sand aus perfekten Kugeln besteht und die Dichten der Körner identisch sind, was in der Realität nicht der Fall ist.
ID:(15061, 0)
Masse eines Schlickkorns
Gleichung 
Sobald wir der Volumen eines Schlickkorns (v_i) und die Dichte eines Schluffkorns (\rho_i) haben, können wir die Masse eines Schlickkorns (m_i) mithilfe der folgenden Gleichung bestimmen:
Es ist jedoch wichtig zu bedenken, dass sowohl das Volumen als auch die Dichte des Schluffkorns Schätzungen sind, wodurch die resultierende Masse hauptsächlich ein Referenzwert ist. Um eine genauere Berechnung zu erhalten, wäre es erforderlich, die Verteilung der Formen und mineralogischen Zusammensetzungen zu untersuchen, um einen präziseren Durchschnittswert zu erhalten.
Es ist relevant zu betonen, dass die berechnete Masse als Referenzpunkt dient, da sie auf der Annahme basiert, dass der Schluff aus perfekten Kugeln besteht und die Dichten der Körner identisch sind, was in der Realität nicht der Fall ist.
ID:(15062, 0)
Masse eines Tonkorns
Gleichung 
Sobald wir der Volumen eines Tonkorns (v_c) und die Dichte eines Tonkorns (\rho_c) haben, können wir die Masse einer Tonplatte (m_c) mithilfe der folgenden Gleichung bestimmen:
Es ist jedoch wichtig zu bedenken, dass sowohl das Volumen als auch die Dichte des Tonkorns Schätzungen sind, wodurch die resultierende Masse hauptsächlich ein Referenzwert ist. Um eine genauere Berechnung zu erhalten, wäre es erforderlich, die Verteilung der Formen und mineralogischen Zusammensetzungen zu untersuchen, um einen präziseren Durchschnittswert zu erhalten.
Es ist relevant zu betonen, dass die berechnete Massenangabe als Referenzpunkt dient, da sie auf der Annahme basiert, dass der Ton aus perfekten Parallelepipeden besteht und die Dichten der Körner identisch sind, was in der Realität nicht der Fall ist.
ID:(15063, 0)
