Soil Components
Storyboard 
The three primary components of soil are sand, silt, and clay. While sand and silt grains are relatively spherical, clay particles resemble small flakes or plates. There is also a significant difference in their sizes: sand grains are just a fraction of a millimeter, silt grains are on the order of microns, and clay particles are even smaller, measuring just a few microns.
This variation in particle sizes has a significant impact on the soil's ability to compact. For instance, clay can fill the spaces between sand and silt grains, influencing the different degrees of compaction that can be achieved in the soil.
ID:(362, 0)
Surface soil
Concept 
When we observe the surface of the soil, we often see some stones or rocks, a brownish mass that we call soil, and some plants.

Field in the 'Bising' area near the village of Oberwilzingen, Swabian Alps, by Ustill (commons.wikimedia.org).
However, upon closer inspection, we'll notice that the soil contains plant remnants, ranging from smaller stones to grains of sand. These decomposed plant remains constitute organic material of a smaller size, sometimes blending with the soil material.
In summary, we can identify:
• Boulders, pebbles, and small rocks.
• Organic matter present in the soil.
• The soil itself.
ID:(15075, 0)
Boulders, cobbles and plebbles
Concept 
In all types of soil, we find boulders, pebbles, and small rocks distributed at various depths. Similarly, as the surface soil erodes, these stones tend to remain on the surface because the surrounding soil has been washed away by surface water flows.

Pebbles on a beach at Broulee, Australia by Steve Shattuck (commons.wikimedia.org)
The concentration of boulders, pebbles, and small rocks varies and affects the mechanical and hydrodynamic properties of the soil. On one hand, rocks in the soil interior stabilize it, providing greater resistance to deformation. On the other hand, due to their lack of porosity, they impede the flow of water, affecting both water flow and moisture transport by diffusion. In this regard, the role of rocks should be taken into account in soil modeling.
ID:(15077, 0)
Organic material
Concept 
Within the pores of the surface soil, there exists organic matter, which includes plant and animal residues, microbial biomass, humus, and substances exuded by the roots.

Do-It-Yourself Guide for Microscopy of Agricultural Soil, Katelyn Solbakk, Mikroliv, Okologisk Landsforening
Within the microbial biomass, we find microorganisms such as bacteria and fungi. Humus, on the other hand, is highly decomposed organic material derived from plant and microbial sources. It significantly enhances the soil's ability to retain nutrients and water.
ID:(15078, 0)
Soil in depth
Concept 
When we observe a cross-section of the soil, we can see the vegetative cover on the surface, and beneath it, the roots that penetrate the top few centimeters of the soil, which contains organic matter. By organic matter, we mean decomposing material, organisms, and microorganisms that thrive in aqueous environments, which is why they inhabit the soil pores where water is present.

Soil cutting in Palos Verdes, Chaihuin, Chile by W.Gerber
As we move further down, we notice that the organic matter gradually diminishes, revealing the underlying soil itself, comprising its three components: sand, silt, and clay, along with rocks. The concentration of these various components varies, creating different layers with distinct physical properties and varying capacities to absorb and transport water.
In summary, in the soil, we can identify components other than organic matter and the primary rocks:
• Sand
• Silt
• Clay
ID:(15076, 0)
Sand
Concept 
Fine sand is a type of soil particle characterized by its relatively small size. It falls between coarser sand particles and finer silt particles in terms of size. Fine sand particles typically range in size from 0.02 to 0.2 millimeters or 20 to 200 micrometers.
Fine sand is commonly found in soil compositions and is characterized by its ability to retain a certain amount of moisture while allowing for reasonable drainage. It can contribute to the soil's texture and affect its ability to support plant growth. Soils with a higher proportion of fine sand tend to have good aeration and drainage properties.

Dunes of Erg Awbari (Idehan Ubari) in the Sahara desert region of the Wadi Al Hayaa District, of the Fezzan region in southwestern Libya by Luca Galuzzi (commons.wikimedia.org)
The chemical composition of sand can vary depending on its origin and mineral composition. Sand is generally composed of various minerals, with quartz being one of the most common. However, the exact chemical composition of sand can vary widely. Here is a general overview of the chemical composition of sand, with approximate percentage ranges:
• Quartz (SiO_2) 90% - 95% [1]: Silicon dioxide, commonly known as silica, is the primary component of most sands. It can make up between 60% and 95% or more of the sand's composition.
• Feldspar (KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8) <10% [1]: Feldspar is another common mineral in sand, and its composition can vary. Potassium feldspar (K-feldspar), sodium feldspar (Na-feldspar), and calcium feldspar (Ca-feldspar) are different types of feldspar minerals found in sand.
• Mica (Muscovite, Biotite) <5% [1]: Mica minerals like muscovite and biotite can range from 1% to 5% or less of the silt composition.
• Other Minerals: Depending on the geological source of the sand, it may contain traces of other minerals such as feldspar, mica, or magnetite.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2080, 0)
Silt
Concept 
Silt is a type of soil particle that falls between sand and clay in terms of particle size. Silt particles typically have a size range between 0.002 and 0.02 millimeters, which is equivalent to 2 to 20 micrometers. These particles are smaller than sand but larger than clay.
A distinctive feature of silt is its ability to retain moisture and nutrients, making it suitable for agriculture. However, it's important to note that silt can become compacted and present drainage issues if it dominates the soil composition. Soils with silt content are often fertile and can support a variety of crops when managed properly.
The chemical composition of silt can vary depending on its origin and geographical location. However, in general terms, silt is composed of various minerals and may contain organic matter. Below, I provide an approximation of the chemical composition of silt in terms of the major elements, expressed as a percentage of the total composition:
• Quartz (SiO_2) 40-60% [1]: Quartz is often the dominant mineral in silt, representing approximately 50% to 70% or even more of its composition.
• Feldspar (KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8) <10% [1]: Feldspar minerals, including potassium feldspar, sodium feldspar, and calcium feldspar, can range from 10% to 30% or more of the composition.
• Mica (Muscovite, Biotite) < 5% [1]: Mica minerals like muscovite and biotite can range from 1% to 5% or less of the silt composition.
• Other Minerals: Silt can contain traces of various other minerals depending on its specific geological origin, such as zircon, garnet, and others.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2068, 0)
Clay
Concept 
Clay is a type of soil particle with very fine particles, typically smaller than 0.002 millimeters or less than 2 micrometers in size. Clay particles are much smaller than sand and silt particles. Clay soils are known for their ability to retain water and nutrients due to their small particle size and high surface area. However, they can also compact easily and may have poor drainage properties. Clay soils can vary in color and texture depending on their mineral composition and organic matter content. They are an important component of many soil types and can influence soil fertility and structure.

Quaternary clay in Estonia (400 000 years old) by Siim Sepp (commons.wikimedia.org)
The chemical composition of clay can vary depending on its specific mineral composition and origin. Clay is primarily composed of tiny mineral particles and generally consists of several minerals, including:
• Kaolinite (Al_2Si_2O_5(OH)_4) 20-40% [1]: Kaolinite is a common clay mineral and the main component of kaolin clay.
• Illite ((K, H_3O)(Al, Mg, Fe)_2(Si, Al)_4O_{10}[(OH)_2,(H_2O)]) 10-40% [1]: Illite is another common clay mineral.
• Smectites/Montmorillonite ((Na, Ca)_{0.33}(Al, Mg)_2(Si_4O_{10})(OH)_2·n(H_2O)) 10-40% [1]: Montmorillonite is a clay mineral known for its swelling properties.
• Chlorite ((Mg, Fe)_3(Si, Al)_4O_{10}(OH)_2·(Mg, Fe)_3(OH)_6) <10% [1]: Chlorite is sometimes found in clay minerals.
• Other Minerals: Additionally, depending on the specific clay deposit, other minerals may also be present in minimal quantities, including quartz, feldspar, and various metal oxides.
[1] Clay Mineralogy, Ralph E. Grim, McGraw-Hill International Series
ID:(2069, 0)
Grain shape
Concept 
To effectively model soil, it's crucial to consider the geometric shapes that best describe the various types of grains that make up the soil.
This involves observing multiple grains of each type. In the case of sand, this can be accomplished using a regular microscope, which allows us to gather collections of grains, as shown below:

Sand grains of yellow building sand. Microscope Lumam R-8. EPI lighting. The photo of each grain of sand is the result of multifocal stacking by Alexander Klepnev (commons.wikimedia.org).
In this instance, we can conclude that the shape is rounded, making it suitable to represent them as spheres.
ID:(2257, 0)
Formation of Sand and Silt Grains
Concept 
Generally, sand grains and silt grains are conglomerates of multiple crystals that are exposed to impacts as they are transported by water or wind. These impacts create fractures along the crystal planes, removing protruding fragments and, as a result, rounding the grain:
The grain becomes rounded as its corners gradually wear away.
In this way, they tend to become more rounded and acquire a shape that resembles small spheres.
ID:(2081, 0)
Formation of Clay Grains
Concept 
Clay grains are typically small crystals exposed to impacts as they are transported by water or wind. These impacts generate fractures along the crystal planes, which, given that the grain is a crystal, implies that it maintains its shape without rounding the corners:
The grain maintains its shape as it tends to wear gradually along the same plane that defines its shape.
Therefore, clay grains are characterized by having a geometric shape similar to small plates resembling straight parallelepipeds.
Therefore, we assume that:
Clay grains are represented as small plates (rectangular parallelepipeds) with equal sides and a given height. It is assumed that all clay grains have the same shape and are identical to each other.
ID:(2083, 0)
Shape of sand grains
Concept 
If we observe the grains under a microscope, we will notice that they have relatively rounded shapes and variable sizes, although they tend to be of a similar size:

Grains of so-called Ottawa Silica Sand under an electron microscope. Magnification 150x. Ottawa Sand is a by-product of hydraulic mining of Ordovician orthoquartzites of the St. Peter Sandstone Formation of the Paleozoic intracratonic Illinois Basin by Nasa (commons.wikimedia.org)
Therefore, in a first approximation, grains can be modeled as spheres:
Grains of sand can be modeled as spheres. To simplify the model, it is assumed that they are all identical. However, a more detailed model could consider the distribution of various radii.
In line with the initial hypothesis that sand grains can be modeled as spheres, their corresponding radius can be introduced.
Therefore, we introduce the radius the sand grain radius (r_a) to describe the spheres of the sand grains.
It should be noted that the radius is an average value, as it varies among different grains.
ID:(15054, 0)
Silt grain shape
Concept 
If we observe the silt grains under a microscope, we will notice that they have relatively cubic shapes and varying sizes, although they tend to be of a similar size:

Initial silt Proctor compaction at optimum wtare content - high magnification, Scanning Electron Microscope (SEM) investigations in soil microstructure description, Dimitri Deneele, 1st IMEKO TC-4 International Workshop on Metrology for Geotechnics, Benevento, Italy, March 17-18, 2016
Therefore, as a first approximation, the grains can be modeled as cubes:
Silt grains can be modeled as cubes. To simplify the model, it is assumed that they are all the same size. However, a more detailed model could consider the distribution of various side lengths.
In line with the initial hypothesis that silt grains can be modeled as cubes, their corresponding side length can be introduced.
Therefore, we introduce the cube side the silt Grain Side (a_i) to describe the grains of silt.
It should be noted that the side length is an average value, as it varies among different grains.
ID:(15056, 0)
Clay grain shape
Concept 
Clay grains are relatively flat and tend to stack in a parallel fashion, as seen in this image obtained through an electron microscope:

SEM image of well crystallized crystallizedkaolinite from sandstone. Note hexagonal morphology,smooth basal surfaces and abundance of slit- andwedge-shaped pores. (The influence of individual clay minerals on formation damage of reservoir sandstones: A critical review with some new insights, Jeff Wilson, L. Wilson, Ian T.M. Patey, May 2014Clay Minerals 49(2))
Their shape resembles flat elements with reduced thickness that resemble rectangular parallelepipeds:
Clay grains can be modeled as rectangular parallelepipeds. To simplify the model, it is assumed that they are all identical. However, a more detailed model could consider the distribution of various lengths and heights.
In line with the initial hypothesis that clay grains can be modeled as rectangular parallelepipeds, their corresponding lengths and height can be introduced.
Therefore, it is introduced to describe the right parallelepiped the length and width of a clay plate (l_c) and the height of a clay plate (w_c).
It should be noted that the lengths and height are average values, as they actually vary among different grains.
ID:(15055, 0)
Sand grain density
Variable 
To calculate the mass of a grain of sand, it is essential to know its density. However, it is important to note that the density of the individual grain differs significantly from the overall density of sand due to its high porosity. Therefore, to estimate the density of a grain of sand, we need to examine the density of its main minerals, as detailed below:
| Mineral | Occurrence | Density [g/cm^3] |
| Quartz | 90-95% [1] | 2.65 [2] |
| Feldspars | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
To develop a simple model, we can assume a homogeneous density:
If we assume that the minerals composing the sand grains are evenly distributed, we can assume that the grains have a constant and uniform density in all of them.
This introduces the density of a grain of sand (\rho_a).
It is important to keep in mind that this value can vary depending on the specific composition of the sand grains.
ID:(15057, 0)
Density of a silt grain
Variable 
To calculate the mass of a silt grain, it is essential to know its density. However, it is important to highlight that the density of the individual grain significantly differs from the density of silt as a whole due to the presence of high porosity in the latter. Therefore, to estimate the density of a silt grain, it is necessary to analyze the density of its main minerals, which are detailed below:
| Mineral | Occurrence | Density [g/cm^3] |
| Quartz | 40-60% [1] | 2.65 [2] |
| Feldspars | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
To develop a simple model, we can assume a homogeneous density:
If we assume that the minerals composing the silt grains are evenly distributed, we can assume that the grains have a constant and uniform density in all of them.
This introduces the density of a grain of silt (\rho_i).
It's important to keep in mind that this value can vary depending on the composition of silt grains.
ID:(15059, 0)
Density of a grain of clay
Variable 
To calculate the mass of a clay grain, it is essential to know its density. However, it's important to note that the density of the individual grain significantly differs from the density of clay as a whole due to the presence of high porosity in the latter. Therefore, to estimate the density of a clay grain, it is necessary to analyze the density of its main minerals, which are detailed below:
| Mineral | Occurrence | Density [g/cm^3] |
| Smectites | 0-80% [1] | 2.75-2.78 [2] |
| Illites | 10-80% [1] | 2.60-2.86 [2] |
| Kaolinites | 20-80% [1] | 2.62-2.66 [2] |
| Chlorites | 0-30% [1] | 2.60-2.96 [2] |
[1] Clay Mineralogy, Ralph E. Grim (1968), McGraw-Hill
[2] Geotechnical Engineering Principles and Practices, Donald P. Coduto et al. (1998), Prentice-Hall
To develop a simple model, we can assume a homogeneous density:
If we assume that the minerals composing the clay grains are evenly distributed, we can assume that the grains have a constant and uniform density in all of them.
This introduces the density of a grain of clay (\rho_c).
It's important to keep in mind that this value can vary depending on the specific composition of clay grains.
ID:(15058, 0)
USGS Chart with Grain Measurements
Image 
The study of the grains in a soil sample involves a comprehensive analysis of various aspects that contribute to understanding the soil's physical properties and behavior. Here's an expanded explanation of the key components of this study:
Size Terms:
- Size terms refer to the categorization of soil particles based on their diameter. Soil particles are typically classified into three main categories:
Sand: The largest particles, with diameters ranging from 0.05 mm to 2 mm.
Silt: Intermediate-sized particles, ranging from 0.002 mm to 0.05 mm.
Clay: The smallest particles, with diameters less than 0.002 mm.
- The relative proportions of these size fractions determine the soil's texture, which, in turn, affects its properties like water retention and drainage.
Sieve Sizes:
- Sieve sizes are standardized mesh sizes used to separate soil particles by size. Common sieve sizes are defined by the ASTM (American Society for Testing and Materials) or ISO (International Organization for Standardization) standards.
- Sieve analysis involves passing a soil sample through a set of sieves with progressively finer mesh sizes to determine the particle size distribution.
Number of Grains per mg:
- This metric represents the density of soil particles within a given mass of soil. It is calculated by counting the number of particles within a known mass of soil (typically 1 mg) and then extrapolating to estimate the total number of particles in a larger sample.
- It provides insights into the population and spacing of soil particles, which can be essential for understanding soil compaction and root penetration.
Settling Velocity:
- Settling velocity refers to the speed at which soil particles fall through a fluid (usually water) under the influence of gravity. It is determined by the size, shape, and density of the particles and the viscosity of the fluid.
- Knowledge of settling velocities is valuable in sedimentation studies and can help predict how long it takes for particles to settle out of suspension in water bodies.
Threshold Velocity for Traction:
- The threshold velocity for traction represents the minimum water flow velocity required to initiate the movement of soil particles on the bed of a stream or river. It is an important parameter in sediment transport studies.
- When water velocity exceeds the threshold velocity for a specific particle size, it can erode and transport those particles, which can have significant environmental implications.
As an example, here is the particle size chart measured in the Long Island Sound by the United States Geological Survey (USGS).
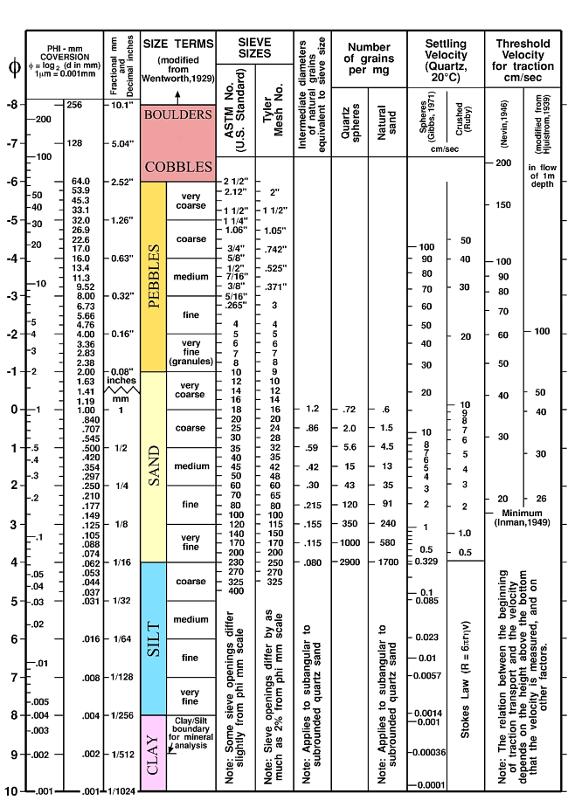
usgs-ofr-00-304
ID:(6941, 0)
Model parameters
Description 
The model can be defined based on the existence of three types of materials (sand, silt, and clay), with grains modeled as follows: in the first two cases, the grains are represented as spheres with different average radii, and in the case of clay, the grains are modeled as straight parallelepipeds.
The parameter ranges are summarized in the following table:
| Type | Parameter | Symbol | Range | Unit |
| Arena | Radio | r_a | 62 - 2000 | \mu m |
| Volume | v_a | 1 - 33500 | nl | |
| Density | \rho_a | 2.64 - 2.69 | g/cm^3 | |
| Mass | m_a | 2.6 - 90100 | \mu g | |
| Slime | Radius | r_i | 4 - 62 | \mu m |
| Volume | v_i | 0.27 - 990 | pl | |
| Density | \rho_i | 2.63 - 2.72 | g/cm^3 | |
| Mass | m_i | 0.71 - 2700 | ng | |
| Clay | Length | l_c | 1 - 4 | \mu m |
| Height | w_c | 0.1 - 0.4 | \mu m | |
| Volume | v_c | 0.1 - 6.4 | fl | |
| Density | \rho_c | 2.66 - 2.80 | g/cm^3 | |
| Mass | m_c | 0.27 - 17.9 | pg |
Since the grains are so small, it is necessary to work in a wide range of dimensions. For this reason, abbreviations are used:
Long
| Symbol | Unit | MKS |
| m | meter | 1 m |
| mm | millimeter | 10^{-3} m |
| \mu m | micrometer | 10^{-6} m |
Volume
| Symbol | Unit | MKS |
| m^3 | cubic meter | 1 m^3 |
| l | liter | 10^{-3} m^3 |
| ml | milliliter | 10^{-6} m^3 |
| \mu l | microliter | 10^{-9} m^3 |
| nl | nanoliter | 10^{-12} m^3 |
| pl | picoliter | 10^{-15} m^3 |
| fl | fentoliter | 10^{-18} m^3 |
Mass
| Symbol | Unit | MKS |
| kg | kilogram | 1 kg |
| g | gram | 10^{-3} kg |
| mg | milligram | 10^{-6} kg |
| \mu g | microgram | 10^{-9} kg |
| ng | nanogram | 10^{-12} kg |
| pg | picogram | 10^{-15} kg |
Density
| Symbol | Unit | MKS |
| kg/m^3 | kilogram per cubic meter | 1 kg/m^3 |
| g/cm^3 | gram per cubic centimeter | 10^{3} kg/m^3 |
ID:(198, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
m_a = \rho_a v_a
m_a = rho_a * v_a
m_c = \rho_c v_c
m_c = rho_c * v_c
m_i = \rho_i v_i
m_i = rho_i * v_i
v_a =\displaystyle\frac{4 \pi }{3} r_a ^3
v_a = 4* pi * r_a ^3/3
v_c = w_c l_c ^2
v_c = w_c * l_c ^2
v_i = a_i ^3
v_i = a_i ^3
ID:(15215, 0)
Volume of a grain of sand
Equation 
If we model a grain of sand as a sphere and assume that the sand grain radius (r_a), we can calculate its the volume grain of sand (v_a) using the equation:
This calculation provides an estimated volume because the radius is an average value. To obtain a more precise calculation or even determine an average volume, it would be necessary to study the distribution of sand grain radii in the study.
It's important to highlight that the calculated volume is only a reference value since it's based on the assumption that the sand consists of perfect and identical spheres, which is not the case in reality.
ID:(4238, 0)
Volume of a grain of silt
Equation 
If we model a grain of silt as a right parallelepiped and assume that the silt Grain Side (a_i), we can calculate its the volume of a grain of silt (v_i) using the following equation:
However, it's important to note that this calculation provides an estimated value of the volume, as the side length is an average value. To obtain a more precise calculation and even determine an average volume, it would be necessary to study the distribution of side lengths of silt grains in the study.
It is relevant to emphasize that the calculated volume serves as a reference value, as it is based on the assumption that silt is composed of perfect and identical cubes, which is not the case in reality.
ID:(15060, 0)
Volume of a clay plate
Equation 
If we model a clay grain as a right parallelepiped and assume it has dimensions of the length and width of a clay plate (l_c) and the height of a clay plate (w_c), we can calculate the volume of a grain of clay (v_c) using the following equation:
However, it's important to note that this calculation provides an estimated volume, as the lengths and height are average values. To obtain a more precise calculation and even determine an average volume, it would be necessary to study the distribution of the lengths and heights of the clay grains in the study.
It's worth emphasizing that the calculated volume serves as a reference value, as it is based on the assumption that the clay is composed of perfect and identical right rectangular parallelepipeds, which may not be the case in reality.
ID:(4239, 0)
Mass of a grain of sand
Equation 
Once we have the volume grain of sand (v_a) and the density of a grain of sand (\rho_a), we can determine the mass of a grain of sand (m_a) by calculating it using the following equation:
However, it's important to remember that both the volume and the density of the sand grain are estimations, so the resulting mass is more of a reference value. A more accurate calculation would require studying the distribution of shapes and mineralogical compositions to obtain a more precise average value.
It's relevant to emphasize that the calculated mass serves as a reference point, as it is based on the assumption that the sand is composed of perfect spheres with identical grain densities, which is not the case in reality.
ID:(15061, 0)
Mass of a grain of silt
Equation 
Once we have the volume of a grain of silt (v_i) and the density of a grain of silt (\rho_i), we can determine the mass of a grain of silt (m_i) using the following equation:
However, it is essential to remember that both the volume and the density of the silt grain are estimates, making the resulting mass primarily a reference value. To obtain a more accurate calculation, it would be necessary to study the distribution of shapes and mineralogical compositions to obtain a more precise average value.
It is relevant to emphasize that the calculated mass serves as a reference point, as it is based on the assumption that silt is composed of perfect spheres and that the densities of the grains are identical, which is not the case in reality.
ID:(15062, 0)
Mass of a grain of clay
Equation 
Once we have the volume of a grain of clay (v_c) and the density of a grain of clay (\rho_c), we can determine the mass of a clay plate (m_c) using the following equation:
However, it is essential to remember that both the volume and the density of the clay grain are estimates, making the resulting mass primarily a reference value. To obtain a more accurate calculation, it would be necessary to study the distribution of shapes and mineralogical compositions to obtain a more precise average value.
It is relevant to emphasize that the calculated mass serves as a reference point, as it is based on the assumption that clay is composed of perfect parallelepipeds and that the densities of the grains are identical, which is not the case in reality.
ID:(15063, 0)
