Componentes do Solo
Storyboard 
As três principais componentes do solo são areia, silte e argila. Enquanto os grãos de areia e silte são relativamente esféricos, as partículas de argila se assemelham a pequenas placas ou lâminas. Além disso, há uma diferença significativa em seus tamanhos: os grãos de areia têm apenas uma fração de milímetro, os grãos de silte têm dimensões da ordem de micrômetros, e as partículas de argila são ainda menores, medindo apenas alguns micrômetros.
Essa variação no tamanho das partículas tem um impacto significativo na capacidade do solo de se compactar. Por exemplo, a argila pode preencher os espaços entre os grãos de areia e silte, influenciando os diferentes graus de compactação que podem ser alcançados no solo.
ID:(362, 0)
Solo superficial
Conceito 
Quando observamos a superfície do solo, frequentemente vemos algumas pedras ou rochas, uma massa marrom que chamamos de solo e algumas plantas.

Campo na área 'Bising' perto da aldeia de Oberwilzingen, na região de Schwäbische Alb, por Ustill (commons.wikimedia.org).
No entanto, ao olharmos com mais atenção, perceberemos que o solo contém restos de plantas, desde pedras menores até grãos de areia. Esses restos de plantas decompostas constituem material orgânico de menor tamanho, às vezes se confundindo com o material do solo circundante.
Em resumo, podemos identificar:
• Pedregulhos, seixos e pequenas pedras.
• Matéria orgânica presente no solo.
• O próprio solo em si.
ID:(15075, 0)
Pedregulhos, seixos, pedrinhas
Conceito 
Em todos os tipos de solo, encontramos pedras grandes, seixos e pequenas pedras distribuídos em várias profundidades. Da mesma forma, à medida que o solo se erode na superfície, essas pedras tendem a permanecer nela, uma vez que o solo ao seu redor foi lavado por fluxos superficiais de água.

Seixos em uma praia em Broulee, Austrália, por Steve Shattuck (commons.wikimedia.org)
A concentração de pedras grandes, seixos e pequenas pedras varia e afeta as propriedades mecânicas e hidrodinâmicas do solo. Por um lado, as rochas no interior do solo estabilizam-no, conferindo-lhe maior resistência à deformação. Por outro lado, devido à falta de porosidade, elas obstruem o fluxo de água, afetando tanto o fluxo de água como o transporte de umidade por difusão. Nesse sentido, o papel das pedras deve ser levado em consideração na modelagem do solo.
ID:(15077, 0)
Matéria orgânica
Conceito 
Dentro dos poros do solo superficial, encontramos matéria orgânica que consiste em resíduos de plantas e animais, biomassa microbiana, húmus e substâncias exsudadas pelas raízes.

Guia faça você mesmo para microscopia de solo agrícola, Katelyn Solbakk, Mikroliv, Okologisk Landsforening
Dentro da biomassa microbiana, encontramos microorganismos como bactérias e fungos. O húmus, por outro lado, é um material orgânico altamente decomposto derivado de fontes vegetais e microbianas. Ele melhora significativamente a capacidade do solo de reter nutrientes e água.
ID:(15078, 0)
Solo em profundidade
Conceito 
Quando observamos um corte no solo, vemos na superfície a vegetação e, abaixo dela, as raízes que penetram os primeiros centímetros do solo, que contém matéria orgânica. Por matéria orgânica, entendemos material em decomposição, organismos e microorganismos que vivem em ambientes aquáticos, por isso eles estão nos poros do solo, onde a água está presente.

Corte de solo em Palos Verdes, Chaihuin, Chile por W.Gerber
Se observarmos nas camadas inferiores, notamos que a matéria orgânica começa a desaparecer e vemos o solo propriamente dito, com suas três componentes: areia, silte e argila, bem como rochas. A concentração dessas diferentes componentes varia, criando diferentes camadas com propriedades físicas distintas e capacidades variadas de absorção e transporte de água.
Resumindo, no solo podemos identificar componentes além da matéria orgânica e das principais rochas:
• Areia
• Silte
• Argila
ID:(15076, 0)
Areia
Conceito 
A areia fina é um tipo de partícula de solo caracterizada pelo seu tamanho relativamente pequeno. Ela se encontra entre as partículas de areia mais grossa e as partículas de silte mais finas em termos de tamanho. As partículas de areia fina geralmente variam em tamanho de 0,02 a 0,2 milímetros ou de 20 a 200 micrômetros.
A areia fina é comumente encontrada na composição do solo e se destaca pela sua capacidade de reter uma certa quantidade de umidade ao mesmo tempo em que permite uma drenagem razoável. Ela pode contribuir para a textura do solo e afetar a sua capacidade de suportar o crescimento das plantas. Solos com uma maior proporção de areia fina tendem a ter boas propriedades de aeração e drenagem.

Dunas de Erg Awbari (Idehan Ubari) na região do deserto do Saara, no Distrito de Wadi Al Hayaa, na região de Fezzan, no sudoeste da Líbia, registradas por Luca Galuzzi (commons.wikimedia.org).
A composição química da areia pode variar dependendo da sua origem e composição mineral. Geralmente, a areia é composta por vários minerais, sendo o quartzo um dos mais comuns. No entanto, a composição química exata da areia pode variar amplamente. Aqui está uma visão geral da composição química da areia, com faixas aproximadas em porcentagem:
• Quartzo ($SiO_2$) 90% - 95% [1]: O dióxido de silício, comumente conhecido como sílica, é o principal componente da maioria das areias. Pode constituir entre 60% e 95% ou mais da composição da areia.
• Feldspato ($KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8$) <10% [1]: O feldspato é outro mineral comum na areia, e sua composição pode variar. O feldspato potássico (K-feldspato), o feldspato sódico (Na-feldspato) e o feldspato cálcico (Ca-feldspato) são diferentes tipos de minerais de feldspato encontrados na areia.
• Mica (Muscovita, Biotita) 1-5% [1]: Minerais de mica, como muscovita e biotita, podem variar de 1% a 5% ou menos da composição do silte.
• Outros Minerais: Dependendo da fonte geológica da areia, podem estar presentes traços de outros minerais, como feldspato, mica ou magnetita.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2080, 0)
Limo
Conceito 
O silte é um tipo de partícula de solo que se situa entre a areia e a argila em termos de tamanho de partícula. As partículas de silte geralmente têm um tamanho que varia entre 0,002 e 0,02 milímetros, o que equivale a 2 a 20 micrômetros. Essas partículas são menores que as de areia, mas maiores do que as de argila.
Uma característica distintiva do silte é a sua capacidade de reter umidade e nutrientes, tornando-o adequado para a agricultura. No entanto, é importante observar que o silte pode compactar-se e apresentar problemas de drenagem se predominar na composição do solo. Solos com teor de silte costumam ser férteis e podem sustentar uma variedade de culturas quando manejados adequadamente.
A composição química do silte pode variar dependendo da origem e da localização geográfica. No entanto, em termos gerais, o silte é composto por diversos minerais e pode conter matéria orgânica. Abaixo, forneço uma aproximação da composição química do silte em termos dos principais elementos, expressos como porcentagem da composição total:
• Quartzo ($SiO_2$) 40-60% [1]: O quartzo costuma ser o mineral dominante no silte, representando aproximadamente entre 50% e 70% ou até mais de sua composição.
• Feldspato ($KAlSi_3O_8 - NaAlSi_3O_8 - CaAl_2Si_2O_8$) <10% [1]: Minerais de feldspato, incluindo feldspato potássico, feldspato sódico e feldspato cálcico, podem variar de 10% a 30% ou mais da composição.
• Mica (Muscovita, Biotita) < 5% [1]: Minerais de mica, como muscovita e biotita, podem variar de 1% a 5% ou menos da composição do silte.
• Outros Minerais: O silte pode conter vestígios de vários outros minerais, dependendo de sua origem geológica específica, como zircão, granada e outros.
[1] Tucker, Maurice E. Year 2001. Sedimentary Petrology. Wiley-Blackwell.
ID:(2068, 0)
Argila
Conceito 
A argila é um tipo de partícula de solo com partículas muito finas, geralmente menores que 0,002 milímetros de tamanho ou menos de 2 micrômetros. As partículas de argila são muito menores do que as partículas de areia e silte. Solos argilosos são conhecidos por sua capacidade de reter água e nutrientes devido ao seu pequeno tamanho de partícula e alta área superficial. No entanto, também podem compactar facilmente e apresentar propriedades de drenagem deficientes. Solos argilosos podem variar em cor e textura, dependendo de sua composição mineral e teor de matéria orgânica. Eles são um componente importante de muitos tipos de solos e podem influenciar a fertilidade e a estrutura do solo.

Argila quaternária na Estônia (com 400.000 anos de idade) por Siim Sepp (commons.wikimedia.org)
A composição química da argila pode variar dependendo de sua composição mineral específica e origem. A argila é principalmente composta por partículas minerais muito pequenas e geralmente consiste em vários minerais, incluindo:
• Caolinita ($Al_2Si_2O_5(OH)_4$) 20-40% [1]: A caolinita é um mineral de argila comum e o principal componente da argila de caulim.
• Iliita ($(K, H_3O)(Al, Mg, Fe)_2(Si, Al)_4O_{10}[(OH)_2,(H_2O)]$) 10-40% [1]: A ilita é outro mineral de argila comum.
• Esmectitas/Montmorilonita ($(Na, Ca)_{0.33}(Al, Mg)_2(Si_4O_{10})(OH)_2·n(H_2O)$) 10-40% [1]: A montmorilonita é um mineral de argila conhecido por suas propriedades de expansão.
• Clorita ($(Mg, Fe)_3(Si, Al)_4O_{10}(OH)_2·(Mg, Fe)_3(OH)_6$) <10% [1]: Às vezes, a clorita é encontrada em minerais de argila.
• Outros Minerais: Além disso, dependendo do depósito específico de argila, outros minerais também podem estar presentes em quantidades mínimas, incluindo quartzo, feldspato e vários óxidos metálicos.
[1] Clay Mineralogy, Ralph E. Grim, McGraw-Hill International Series
ID:(2069, 0)
Formato de grão
Conceito 
Para modelar o solo de forma eficaz, é fundamental considerar as formas geométricas que melhor descrevem os diversos tipos de grãos que compõem o solo.
Para isso, é necessário observar múltiplos grãos de cada tipo. No caso da areia, isso é possível com um microscópio comum, o que permite reunir coleções de grãos, conforme mostrado abaixo:

Grãos de areia de areia de construção amarela. Microscópio Lumam R-8. Iluminação EPI. A foto de cada grão de areia é o resultado de empilhamento multifocal por Alexander Klepnev (commons.wikimedia.org).
Neste caso, podemos concluir que a forma é arredondada, o que nos permite representá-los eficazmente como esferas.
ID:(2257, 0)
Formação de grãos de areia e lodo
Conceito 
Geralmente, os grãos de areia e os grãos de silte são conglomerados de múltiplos cristais que estão expostos a impactos à medida que são transportados pela água ou pelo vento. Esses impactos criam fraturas ao longo dos planos cristalinos, removendo fragmentos salientes e, como resultado, arredondando o grão:
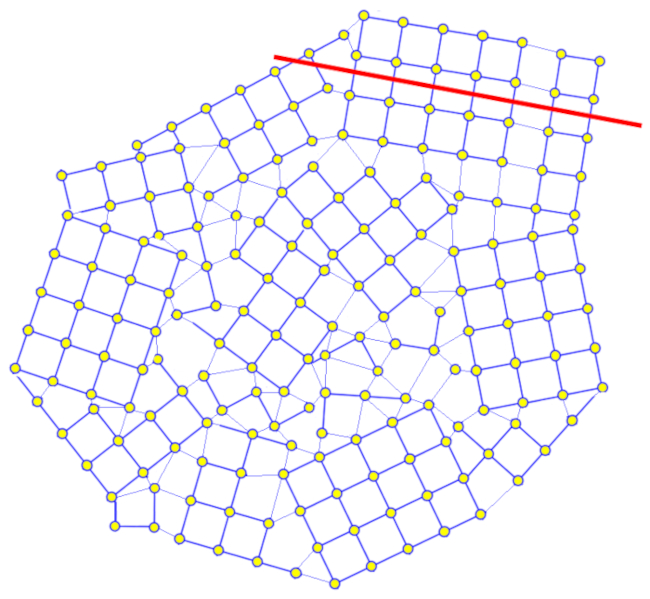
O grão vai se tornando arredondado à medida que seus cantos desgastam gradualmente.
Dessa forma, eles tendem a se tornar mais arredondados e adquirem uma forma que se assemelha a pequenas esferas.
ID:(2081, 0)
Formação de Grãos de Argila
Conceito 
Os grãos de argila geralmente são pequenos cristais expostos a impactos à medida que são transportados pela água ou pelo vento. Esses impactos geram fraturas ao longo dos planos cristalinos, o que, dado que o grão é um cristal, implica que ele mantenha sua forma sem arredondar os cantos:
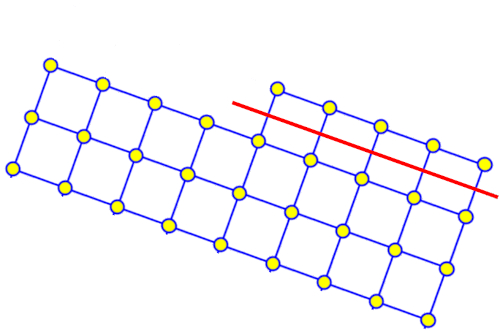
O grão mantém sua forma, pois tende a desgastar gradualmente ao longo do mesmo plano que define sua forma.
Portanto, os grãos de argila se caracterizam por ter uma forma geométrica semelhante a pequenas placas que se assemelham a paralelepípedos retos.
ID:(2083, 0)
Formato dos grãos de areia
Conceito 
Se observarmos os grãos sob um microscópio, notaremos que eles têm formas relativamente arredondadas e tamanhos variáveis, embora tendam a ser de tamanho semelhante:

Grãos da chamada 'Areia de Sílica de Ottawa' sob um microscópio eletrônico. Aumento de 150x. A 'Areia de Ottawa' é um subproduto da mineração hidráulica de ortoquartzitos ordovicianos da Formação da Arenito de São Pedro na Bacia Intracratônica de Illinois do Paleozoico, realizada pela NASA (commons.wikimedia.org).
Portanto, em uma primeira aproximação, os grãos podem ser modelados como esferas:
Os grãos de areia podem ser modelados como esferas. Para simplificar o modelo, assume-se que todos são idênticos. No entanto, um modelo mais detalhado poderia considerar a distribuição de vários raios.
Em conformidade com a hipótese inicial de que os grãos de areia podem ser modelados como esferas, pode-se introduzir o seu raio correspondente.
Portanto, introduzimos o raio o raio do grão de areia ($r_a$) para descrever as esferas dos grãos de areia.
Deve-se observar que o raio é um valor médio, uma vez que varia entre diferentes grãos.
ID:(15054, 0)
Forma de grão de limo
Conceito 
Se observarmos os grãos de silte sob um microscópio, notaremos que eles têm formas relativamente cúbicas e tamanhos variados, embora tendam a ter um tamanho semelhante:

Initial silt Proctor compaction at optimum wtare content - high magnification, Scanning Electron Microscope (SEM) investigations in soil microstructure description, Dimitri Deneele, 1st IMEKO TC-4 International Workshop on Metrology for Geotechnics, Benevento, Italy, March 17-18, 2016
Portanto, como uma primeira aproximação, os grãos podem ser modelados como cubos:
Os grãos de silte podem ser modelados como cubos. Para simplificar o modelo, assume-se que todos têm o mesmo tamanho. No entanto, um modelo mais detalhado poderia considerar a distribuição de diferentes comprimentos de lado.
Em linha com a hipótese inicial de que os grãos de silte podem ser modelados como cubos, pode-se introduzir o comprimento de lado correspondente.
Portanto, introduzimos o lado do cubo o lado de grão de lodo ($a_i$) para descrever os grãos de silte.
Deve-se observar que o comprimento do lado é um valor médio, pois varia entre diferentes grãos.
ID:(15056, 0)
Formato de grão de argila
Conceito 
Os grãos de argila são relativamente planos e tendem a se empilhar de forma paralela, como observado nesta imagem obtida por meio de um microscópio eletrônico:

SEM image of well crystallized crystallizedkaolinite from sandstone. Note hexagonal morphology,smooth basal surfaces and abundance of slit- andwedge-shaped pores. (The influence of individual clay minerals on formation damage of reservoir sandstones: A critical review with some new insights, Jeff Wilson, L. Wilson, Ian T.M. Patey, May 2014Clay Minerals 49(2))
A forma deles se assemelha a elementos planos com espessura reduzida que se assemelham a paralelepípedos retangulares:
Os grãos de argila podem ser modelados como paralelepípedos retangulares. Para simplificar o modelo, assume-se que todos são idênticos. No entanto, um modelo mais detalhado poderia considerar a distribuição de várias medidas de comprimento e altura.
De acordo com a hipótese inicial de que os grãos de argila podem ser modelados como paralelepípedos retangulares, suas medidas de comprimento e altura correspondentes podem ser introduzidas.
Portanto, é introduzido para descrever o paralelepípedo reto o comprimento e largura de uma placa de argila ($l_c$) e la altura de um prato de barro ($w_c$).
Deve-se observar que as medidas de comprimento e altura são valores médios, uma vez que realmente variam entre diferentes grãos.
ID:(15055, 0)
Densidade de grãos de areia
Variable 
Para calcular a massa de um grão de areia, é essencial conhecer a sua densidade. No entanto, é importante notar que a densidade do grão individual difere significativamente da densidade geral da areia devido à sua alta porosidade. Portanto, para estimar a densidade de um grão de areia, é necessário examinar a densidade dos seus principais minerais, conforme detalhado abaixo:
| Mineral | Ocorrência | Densidade [$g/cm^3$] |
| Quartzo | 90-95% [1] | 2.65 [2] |
| Feldspatos | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Para desenvolver um modelo simples, podemos assumir uma densidade homogênea:
Se supusermos que os minerais que compõem os grãos de areia estão distribuídos de maneira homogênea, podemos assumir que os grãos têm uma densidade constante e uniforme em todos eles.
Isso apresenta la densidade de um grão de areia ($\rho_a$).
É importante ter em mente que esse valor pode variar dependendo da composição específica dos grãos de areia.
ID:(15057, 0)
Densidade de um grão de lodo
Variable 
Para calcular a massa de um grão de silte, é essencial conhecer a sua densidade. No entanto, é importante destacar que a densidade do grão em si difere significativamente da densidade do silte como um todo, devido à presença de alta porosidade neste último. Portanto, para estimar a densidade de um grão de silte, é necessário analisar a densidade de seus principais minerais, que são detalhados abaixo:
| Mineral | Ocorrência | Densidade [$g/cm^3$] |
| Quartzo | 40-60% [1] | 2.65 [2] |
| Feldspatos | <10% [1] | 2.50-2.80 [2] |
| Micas | <5% [1] | 2.70-3.30 [2] |
[1] Sedimentary Petrology, Tucker, Maurice E. (2001). Wiley-Blackwell.
[2] Manual of Mineralogy (22nd ed.), Klein, C., & Hurlbut, C. S. Jr. (1993). John Wiley & Sons.
Para desenvolver um modelo simples, podemos assumir uma densidade homogênea:
Se supusermos que os minerais que compõem os grãos de limo estão distribuídos de maneira homogênea, podemos assumir que os grãos têm uma densidade constante e uniforme em todos eles.
Isso apresenta la densidade de um grão de lodo ($\rho_i$).
É importante ter em mente que esse valor pode variar dependendo da composição dos grãos de silte.
ID:(15059, 0)
Densidade de um grão de argila
Variable 
Para calcular a massa de um grão de argila, é fundamental conhecer a sua densidade. No entanto, é crucial destacar que a densidade do grão em si difere significativamente da densidade da argila como um todo, devido à notável presença de alta porosidade nesta última. Portanto, para estimar a densidade de um grão de argila, é necessário analisar a densidade dos seus principais minerais, que são detalhados a seguir:
| Mineral | Ocorrência | Densidade [$g/cm^3$] |
| Esmectitas | 0-80% [1] | 2.75-2.78 [2] |
| Ilitas | 10-80% [1] | 2.60-2.86 [2] |
| Caolinitas | 20-80% [1] | 2.62-2.66 [2] |
| Cloreto | 0-30% [1] | 2.60-2.96 [2] |
[1] Clay Mineralogy, Ralph E. Grim (1968), McGraw-Hill
[2] Geotechnical Engineering Principles and Practices, Donald P. Coduto et al. (1998), Prentice-Hall
Para desenvolver um modelo simples, podemos assumir uma densidade homogênea:
Se supusermos que os minerais que compõem os grãos de argila estão distribuídos de maneira homogênea, podemos assumir que os grãos têm uma densidade constante e uniforme em todos eles.
Isso apresenta la comprimento e largura de uma placa de argila ($\rho_c$).
É importante ter em mente que esse valor pode variar de acordo com a composição específica dos grãos de argila.
ID:(15058, 0)
Gráfico USGS com medições de grãos
Imagem 
O estudo dos grãos em uma amostra de solo envolve uma análise abrangente de vários aspectos que contribuem para a compreensão das propriedades físicas e do comportamento do solo. Aqui está uma explicação detalhada dos principais componentes deste estudo:
Termos de Tamanho:
- Termos de tamanho referem-se à categorização das partículas do solo com base em seu diâmetro. As partículas do solo geralmente são classificadas em três categorias principais:
Areia: As maiores partículas, com diâmetros variando de 0,05 mm a 2 mm.
Silte: Partículas de tamanho intermediário, variando de 0,002 mm a 0,05 mm.
Argila: As menores partículas, com diâmetros inferiores a 0,002 mm.
- As proporções relativas dessas frações de tamanho determinam a textura do solo, que, por sua vez, afeta suas propriedades, como retenção de água e drenagem.
Tamanhos de Peneira:
- Tamanhos de peneira são tamanhos de malha padronizados usados para separar partículas do solo por tamanho. Tamanhos comuns de peneira são definidos pelas normas da ASTM (Sociedade Americana de Testes e Materiais) ou da ISO (Organização Internacional de Normalização).
- A análise de peneira envolve a passagem de uma amostra de solo por um conjunto de peneiras com malhas progressivamente mais finas para determinar a distribuição do tamanho das partículas.
Número de Grãos por mg:
- Essa métrica representa a densidade de partículas do solo dentro de uma massa de solo conhecida. Ela é calculada contando o número de partículas dentro de uma massa conhecida de solo (geralmente 1 mg) e depois extrapolando para estimar o número total de partículas em uma amostra maior.
- Fornece informações sobre a população e o espaçamento das partículas do solo, o que pode ser essencial para entender a compactação do solo e a penetração das raízes.
Velocidade de Sedimentação:
- A velocidade de sedimentação refere-se à velocidade com que as partículas do solo caem através de um fluido (geralmente água) sob a influência da gravidade. Ela é determinada pelo tamanho, forma e densidade das partículas e pela viscosidade do fluido.
- O conhecimento das velocidades de sedimentação é valioso em estudos de sedimentação e pode ajudar a prever quanto tempo leva para que as partículas se sedimentem fora da suspensão em corpos d'água.
Velocidade Limite para Tração:
- A velocidade limite para tração representa a velocidade mínima do fluxo de água necessária para iniciar o movimento de partículas do solo no leito de um riacho ou rio. É um parâmetro importante em estudos de transporte de sedimentos.
- Quando a velocidade da água ultrapassa a velocidade limite para um tamanho de partícula específico, ela pode erosionar e transportar essas partículas, o que pode ter implicações ambientais significativas.
Como exemplo, aqui está o gráfico de tamanho de partículas medido no Long Island Sound pelo Serviço Geológico dos Estados Unidos (USGS).
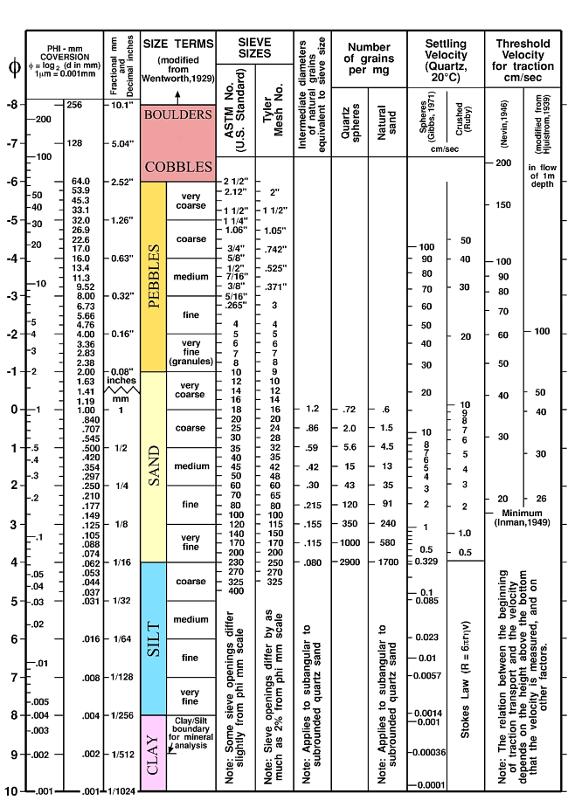
usgs-ofr-00-304
ID:(6941, 0)
Parâmetros do modelo
Descrição 
O modelo pode ser definido com base na existência de três tipos de materiais (areia, silte e argila), com grãos modelados da seguinte forma: nos dois primeiros casos, os grãos são representados como esferas com diferentes raios médios, e no caso da argila, os grãos são modelados como paralelepípedos retos.
Os intervalos de parâmetros estão resumidos na seguinte tabela:
| Tipo | Parâmetro | Símbolo | Faixa | Unidade |
| Arena | Rádio | $r_a$ | 62 - 2000 | $\mu m$ |
| Volume | $v_a$ | 1 - 33500 | $nl$ | |
| Densidade | $\rho_a$ | 2,64 - 2,69 | $g/cm^3$ | |
| Massa | $m_a$ | 2,6 - 90100 | $\mu g$ | |
| Slime | Raio | $r_i$ | 4 - 62 | $\mu m$ |
| Volume | $v_i$ | 0,27 - 990 | $pl$ | |
| Densidade | $\rho_i$ | 2,63 - 2,72 | $g/cm^3$ | |
| Massa | $m_i$ | 0,71 - 2700 | $ng$ | |
| Argila | Comprimento | $l_c$ | 1 - 4 | $\mu m$ |
| Altura | $w_c$ | 0,1 - 0,4 | $\mu m$ | |
| Volume | $v_c$ | 0,1 - 6,4 | $fl$ | |
| Densidade | $\rho_c$ | 2,66 - 2,80 | $g/cm^3$ | |
| Massa | $m_c$ | 0,27 - 17,9 | $pg$ |
Como os grãos são tão pequenos, é necessário trabalhar em diversas dimensões. Por esse motivo, são utilizadas abreviaturas:
Longo
| Símbolo | Unidade | MKS |
| $m$ | metro | $1 m$ |
| $mm$ | milímetro | $10^{-3} m$ |
| $\mu m$ | micrômetro | $10^{-6} m$ |
Volume
| Símbolo | Unidade | MKS |
| $ m ^ 3 $ | metro cúbico | $ 1 m ^ 3 $ |
| $l$ | litro | $10^{-3} m^3$ |
| $ml$ | mililitro | $10^{-6} m^3$ |
| $\mu l$ | microlitro | $10^{-9} m^3$ |
| $nl$ | nanolitro | $10^{-12} m^3$ |
| $pl$ | picolitro | $10^{-15} m^3$ |
| $fl$ | fentolitro | $10^{-18} m^3$ |
Massa
| Símbolo | Unidade | MKS |
| $kg$ | quilograma | $1 kg$ |
| $g$ | grama | $10^{-3} kg$ |
| $mg$ | miligrama | $10^{-6} kg$ |
| $\mu g$ | micrograma | $10^{-9} kg$ |
| $ng$ | nanograma | $10^{-12} kg$ |
| $pg$ | picograma | $10^{-15} kg$ |
Densidade
| Símbolo | Unidade | MKS |
| $kg/m^3$ | quilograma por metro cúbico | $1 kg/m^3$ |
| $g/cm^3$ | grama por centímetro cúbico | $10^{3} kg/m^3$ |
ID:(198, 0)
Modelo
Top 
Parâmetros
Variáveis
Cálculos
Cálculos
Cálculos
Equações
$ m_a = \rho_a v_a $
m_a = rho_a * v_a
$ m_c = \rho_c v_c $
m_c = rho_c * v_c
$ m_i = \rho_i v_i $
m_i = rho_i * v_i
$ v_a =\displaystyle\frac{4 \pi }{3} r_a ^3$
v_a = 4* pi * r_a ^3/3
$ v_c = w_c l_c ^2$
v_c = w_c * l_c ^2
$ v_i = a_i ^3$
v_i = a_i ^3
ID:(15215, 0)
Volume de um grão de areia
Equação 
Se modelarmos um grão de areia como uma esfera e assumirmos que o raio do grão de areia ($r_a$), podemos calcular seu o volume de um grão de areia ($v_a$) usando a equação:
Essa calculação fornece um valor estimado do volume, uma vez que o raio é um valor médio. Para obter um cálculo mais preciso ou até mesmo determinar um volume médio, seria necessário estudar a distribuição dos raios dos grãos de areia no estudo.
É importante destacar que o volume calculado é apenas um valor de referência, pois se baseia na suposição de que a areia consiste em esferas perfeitas e idênticas, o que não é o caso na realidade.
ID:(4238, 0)
Volume de um grão de lodo
Equação 
Se modelarmos um grão de silte como um paralelepípedo reto e assumirmos que o lado de grão de lodo ($a_i$), podemos calcular seu o volume de um grão de lodo ($v_i$) usando a seguinte equação:
No entanto, é importante observar que esse cálculo fornece um valor estimado do volume, uma vez que o lado é um valor médio. Para obter um cálculo mais preciso e até mesmo determinar um volume médio, seria necessário estudar a distribuição dos tamanhos dos lados dos grãos de silte no estudo.
É relevante enfatizar que o volume calculado serve como um valor de referência, pois se baseia na suposição de que o silte é composto por cubos perfeitos e idênticos, o que não corresponde à realidade.
ID:(15060, 0)
Volume de uma placa de barro
Equação 
Se modelarmos um grão de argila como um paralelepípedo reto e assumirmos que ele possui as dimensões o comprimento e largura de uma placa de argila ($l_c$) e la altura de um prato de barro ($w_c$), podemos calcular o volume de um grão de barro ($v_c$) usando a seguinte equação:
No entanto, é importante destacar que esse cálculo fornece um valor estimado do volume, já que os comprimentos e a altura são valores médios. Para obter um cálculo mais preciso e até mesmo determinar um volume médio, seria necessário estudar a distribuição dos comprimentos e alturas dos grãos de argila no estudo.
É relevante enfatizar que o volume calculado serve como um valor de referência, pois se baseia na suposição de que a argila é composta por paralelepípedos retos perfeitos e idênticos, o que pode não ser o caso na realidade.
ID:(4239, 0)
Volume de um grão de areia
Equação 
Uma vez que temos o volume de um grão de areia ($v_a$) e la densidade de um grão de areia ($\rho_a$), podemos determinar la massa de um grão de areia ($m_a$) calculando-o usando a seguinte equação:
No entanto, é importante lembrar que tanto o volume quanto a densidade do grão de areia são estimativas, tornando a massa resultante principalmente um valor de referência. Para realizar um cálculo mais preciso, seria necessário estudar a distribuição das formas e composições mineralógicas para obter um valor médio mais exato.
É relevante ressaltar que a massa calculada serve como um ponto de referência, uma vez que se baseia na suposição de que a areia é composta por esferas perfeitas e que as densidades dos grãos são idênticas, o que não é o caso na realidade.
ID:(15061, 0)
Massa de um grão de lodo
Equação 
Uma vez que temos o volume de um grão de lodo ($v_i$) e la densidade de um grão de lodo ($\rho_i$), podemos determinar la massa de um grão de lodo ($m_i$) usando a seguinte equação:
No entanto, é fundamental lembrar que tanto o volume quanto a densidade do grão de silte são estimativas, tornando a massa resultante principalmente um valor de referência. Para obter um cálculo mais preciso, seria necessário estudar a distribuição das formas e composições mineralógicas para obter um valor médio mais exato.
É relevante destacar que a massa calculada serve como um ponto de referência, uma vez que se baseia na suposição de que o silte é composto por esferas perfeitas e que as densidades dos grãos são idênticas, o que não é o caso na realidade.
ID:(15062, 0)
Massa de um grão de barro
Equação 
Uma vez que temos o volume de um grão de barro ($v_c$) e la comprimento e largura de uma placa de argila ($\rho_c$), podemos determinar la massa de um prato de barro ($m_c$) usando a seguinte equação:
No entanto, é fundamental lembrar que tanto o volume quanto a densidade do grão de argila são estimativas, tornando a massa resultante principalmente um valor de referência. Para obter um cálculo mais preciso, seria necessário estudar a distribuição das formas e composições mineralógicas para obter um valor médio mais exato.
É relevante destacar que a massa calculada serve como um ponto de referência, uma vez que se baseia na suposição de que a argila é composta por paralelepípedos perfeitos e que as densidades dos grãos são idênticas, o que não é o caso na realidade.
ID:(15063, 0)
