Benützer:
Indikatoren
Storyboard 
Die Existenz von Poren ist eines der Schlüsselelemente für das Verhalten des Bodens. Einerseits ermöglichen Poren die Bewegung von Wasser und/oder Feuchtigkeit durch den Boden, andererseits beeinflussen sie jedoch die mechanischen Eigenschaften des Bodens.
Daher ist es wichtig, Indikatoren zu haben, die das Vorhandensein von Porosität beschreiben und den Anteil des in den Poren enthaltenen Wassers angeben. Diese Indikatoren sind entscheidend für die Charakterisierung der hydraulischen, thermodynamischen und mechanischen Eigenschaften des Bodens.
ID:(365, 0)
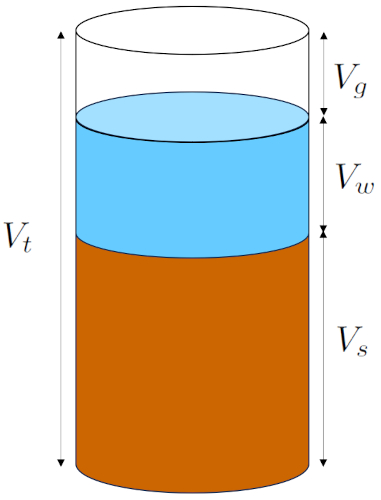
Modell von Feststoffvolumen, Wasser und Gas
Konzept
Im Bodenmodell besteht das Gesamtvolumen ($V_t$) der Probe aus drei Hauptkomponenten:
• das Solides Volumen ($V_s$): Diese Komponente umfasst das Volumen aller im Probenmaterial vorhandenen Körner.
• der Water Volume ($V_w$): Stellt das Volumen des im Boden sowohl in den Mikroporen als auch in den Makroporen enthaltenen Wassers dar.
• der Gasvolumen ($V_g$): Umfasst das Volumen des im Probenmaterial enthaltenen Gases oder Luft.
Die folgende Abbildung fasst diese Beschreibung zusammen:
None
ID:(1642, 0)
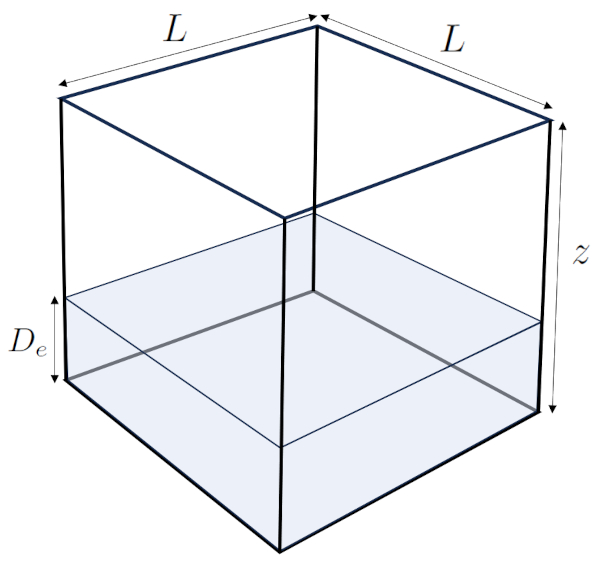
Darstellung der effektiven Tiefe
Bild
Die Effektive Tiefe ($D_e$) bezieht sich auf die Tiefe, die das im Boden enthaltene Wasser erreichen würde, wenn das gesamte feste Volumen "entfernt" würde, wie in der folgenden Abbildung dargestellt:
None
Dies bietet eine intuitive Maßnahme für den Wassergehalt im Boden.
ID:(1641, 0)
Massenmodell Fest, Wasser und Gas
Konzept
Im Bodenmodell besteht die Gesamtmasse ($M_t$) der Probe aus drei Hauptkomponenten:
• die Gesamttrockenmasse der Probe ($M_s$): Dieser Bestandteil umfasst die Massen aller in der Probe vorhandenen Körner.
• die Wassermasse im Boden ($M_w$): Stellt die Masse des im Boden enthaltenen Wassers sowohl in den Mikroporen als auch in den Makroporen dar.
• die Gasmasse im Boden ($M_g$): Umfasst die Masse des Gases oder der Luft, das in der Probe enthalten ist (was vergleichsweise als nahezu null betrachtet werden kann, d.h. $M_g\sim 0$).
ID:(2084, 0)
Innenfläche
Konzept
Eine der unterscheidenden Eigenschaften von Partikeln, wie zum Beispiel Boden, ist ihre innere Oberfläche. Unter innerer Oberfläche verstehen wir die Summe aller Oberflächen jedes einzelnen Korns. Diese Oberfläche ist einer der Schlüsselfaktoren zur Untersuchung des Feuchtigkeitsverhaltens und des Vorhandenseins von Nährstoffen im Boden.
Wenn wir die Oberfläche jedes Korns mit seiner Menge multiplizieren, erhalten wir die Gesamtoberfläche. Um die Oberfläche jedes Korns zu bestimmen, ist es wichtig, seine Form zu berücksichtigen. Es ist wichtig zu beachten, dass sowohl Sand als auch Schluff als Kugeln modelliert werden, während Ton als ein gerader Parallelepiped dargestellt wird.
ID:(1540, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ D_e = \theta_V z $
D_e = theta_V * z
$ e =\displaystyle\frac{ V_g + V_w }{ V_s }$
e =( V_g + V_w )/ V_s
$ f_g =\displaystyle\frac{ V_g }{ V_t }$
f_g = V_g / V_t
$ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$
g_M = S_t / M_s
$ M_t = M_s + M_w $
M_t = M_s + M_w
$ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$
Phi = 1 - rho_b / rho_p
$ \rho_b =\displaystyle\frac{ M_s }{ V_t }$
rho_b = M_s / V_t
$ \rho_w =\displaystyle\frac{ M_w }{ V_w }$
rho_w = M_w / V_w
$ S = \displaystyle\frac{ \theta_V }{ \Phi }$
S = theta_V / Phi
$ S_a = N_a s_a $
S_a = N_a * s_a
$ s_c = 2 l_c ^2 + 4 w_c l_c $
s_c = 2* l_c ^2 + 4* w_c * l_c
$ S_c = N_c s_c $
S_c = N_c * s_c
$ s_i = 6 a_i ^2 $
s_i = 6* a_i ^2
$ S_i = N_i s_i $
S_i = N_i * s_i
$ S_t = S_a + S_l + S_c $
S_t = S_a + S_l + S_c
$ \theta_r =\displaystyle\frac{ V_w }{ V_s }$
theta_r = V_w / V_s
$ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$
theta_s = V_w /( V_g + V_w )
$ \theta_V =\displaystyle\frac{ V_w }{ V_t }$
theta_V = V_w / V_t
$ \theta_w =\displaystyle\frac{ M_w }{ M_s }$
theta_w = M_w / M_s
$ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$
V_g = S_t / V_t
$ V_p = V_w + V_g $
V_p = V_w + V_g
$ V_t = V_s + V_w + V_g $
V_t = V_s + V_w + V_g
$ s_a = 4 \pi r_a ^2 $
s_k = 4* pi * r_a ^2
ID:(15219, 0)
Gesamtvolumen mit Wasser
Gleichung
Das Gesamtvolumen ($V_t$) wird durch Addition des festen Teils der Körner, der das Solides Volumen ($V_s$) entspricht, zu dem im der Water Volume ($V_w$) enthaltenen Wasser und der Luft oder allgemein des Gases im der Gasvolumen ($V_g$) erhalten:
| $ V_t = V_s + V_w + V_g $ |
ID:(15089, 0)
Porenvolumen
Gleichung
Der Porenvolumen ($V_p$) ist nicht notwendigerweise leer; er kann insbesondere Wasser enthalten, daher führen wir die Variable der Water Volume ($V_w$) ein. Andererseits wird das verbleibende Volumen als der Gasvolumen ($V_g$) betrachtet.
Auf diese Weise wird das der Porenvolumen ($V_p$) als Summe beider Volumina berechnet:
| $ V_p = V_w + V_g $ |
ID:(4723, 0)
Volumenverhältnis des Bodenwassers
Gleichung
Ein Indikator, der den Anteil des Wassers am Gesamtvolumen der Probe angibt, ist die Beziehung Volumen Wasser Land ($\theta_V$). Dieser wird berechnet, indem das Verhältnis zwischen der Water Volume ($V_w$) und das Gesamtvolumen ($V_t$) geschätzt wird:
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
ID:(4721, 0)
Volumenverhältnis von festem Wasser
Gleichung
Ein Indikator, der den Anteil des Wassers am festen Volumen der Probe angibt, ist die Beziehung Volumenwasser Solido ($\theta_r$). Dieser wird berechnet, indem das Verhältnis zwischen der Water Volume ($V_w$) und das Solides Volumen ($V_s$) geschätzt wird:
| $ \theta_r =\displaystyle\frac{ V_w }{ V_s }$ |
ID:(4722, 0)
Hohlraumverhältnis
Gleichung
Das Verhältnis zwischen dem Volumen des Wassers und dem Volumen des Feststoffs vergleicht die Menge des Wassers mit der Menge des Feststoffs im Boden. Da sich jedoch das Volumen des Wassers ändern kann, ist es interessant, der Porenvolumen ($V_p$) oder alternativ die Summe von der Gasvolumen ($V_g$) und der Water Volume ($V_w$) mit das Solides Volumen ($V_s$) zu vergleichen, um den Indikator die Hohlraumverhältnis ($e$) wie folgt zu definieren:
| $ e =\displaystyle\frac{ V_g + V_w }{ V_s }$ |
ID:(4728, 0)
Luftporosität
Gleichung
Die Porosität ($f$) wird als das Verhältnis zwischen der Porenvolumen ($V_p$) und das Gesamtvolumen ($V_t$) definiert. Ebenso wird die Luftporosität ($f_g$) basierend auf dem Volumen, das nicht von Wasser eingenommen wird, definiert, nämlich als das Verhältnis zwischen der Gasvolumen ($V_g$) und das Gesamtvolumen ($V_t$):
| $ f_g =\displaystyle\frac{ V_g }{ V_t }$ |
ID:(4724, 0)
Relative Sättigung
Gleichung
Die Relative Sättigung ($\theta_s$) wird berechnet als Anteil der Porosität, der durch Wasser definiert ist (der Water Volume ($V_w$) geteilt durch die Summe von der Water Volume ($V_w$) und der Gasvolumen ($V_g$)), ausgedrückt durch:
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
ID:(4727, 0)
Effektive Tiefe
Gleichung
Die Beziehung Volumen Wasser Land ($\theta_V$) ermöglicht es uns, die Effektive Tiefe ($D_e$) abzuschätzen, die das Wasser erreichen würde, wenn der Boden auf eine Tiefe von die Tiefe ($z$) entfernt würde, was mit folgender Gleichung berechnet wird:
| $ D_e = \theta_V z $ |
Wenn Sie ein Volumen Erde mit Breite und Länge $L$ und die Tiefe ($z$) haben, wird sein Volumen durch die folgende Gleichung dargestellt:
$V_t = L^2z$
Mit die Effektive Tiefe ($D_e$), das eine wichtige Variable repräsentiert, kann das Volumen des Wassers wie folgt berechnet werden:
$V_w = L^2D_e$
Darüber hinaus können wir mit der Gleichung
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
diese Variablen wie folgt in Beziehung setzen:
$\theta_V = \displaystyle\frac{V_w}{V_t} = \displaystyle\frac{D_e}{z}$
Daher kann die Variable die Effektive Tiefe ($D_e$) mit dem folgenden Ausdruck berechnet werden:
| $ D_e = \theta_V z $ |
ID:(3231, 0)
Gesamtmasse
Gleichung
Die Gesamtmasse ($M_t$) wird berechnet, indem die Gesamttrockenmasse der Probe ($M_s$) und die Wassermasse im Boden ($M_w$) addiert werden, wie folgt:
| $ M_t = M_s + M_w $ |
ID:(4247, 0)
Scheinbare Dichte
Gleichung
Im Allgemeinen wird die Dichte als Verhältnis von Masse zu Volumen eines Materials definiert. Im Fall von Boden, der Porosität enthält, wenn das Gesamtvolumen ($V_t$) verwendet wird, werden das Solides Volumen ($V_s$), der Water Volume ($V_w$) und der Porenvolumen ($V_p$) einbezogen. Normalerweise wird die scheinbare Dichte für trockenes Material berechnet, d.h., ohne Wasser ($M_w \sim 0$), sodass die Gesamtmasse ($M_t$) gleich die Gesamttrockenmasse der Probe ($M_s$) ist:
$M_t\sim M_s$
Es ist wichtig zu beachten, dass dies eine Annäherung ist, da beim Trocknen des Bodens immer eine geringe Menge Wasser zurückbleibt, was es sehr schwierig macht, die Masse des Feststoffs ohne Wasser genau zu messen.
Daher definieren wir die Trockenschüttdichte ($\rho_b$) als das Verhältnis von die Wassermasse im Boden ($M_w$) zu das Gesamtvolumen ($V_t$):
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
ID:(4719, 0)
Wasserdichte
Gleichung
Bei der Arbeit mit Wasser ist es auch entscheidend, die Variable die Wasserdichte ($\rho_w$) zu berücksichtigen, die mithilfe von die Wassermasse im Boden ($M_w$) und der Water Volume ($V_w$) mit folgender Gleichung berechnet wird:
| $ \rho_w =\displaystyle\frac{ M_w }{ V_w }$ |
ID:(4730, 0)
Gravimetrisches Wasser-Feststoff-Verhältnis
Gleichung
Wenn wir angeben möchten, in welchem Maße der Boden Wasser enthält, können wir einen Indikator namens die Beziehung gravimetrische Wasser Solido ($\theta_w$) einführen, der als Verhältnis von die Wassermasse im Boden ($M_w$) zu die Gesamttrockenmasse der Probe ($M_s$) berechnet wird, unter Verwendung der folgenden Gleichung:
| $ \theta_w =\displaystyle\frac{ M_w }{ M_s }$ |
ID:(4720, 0)
Oberfläche eines Sandkorns
Gleichung
Da wir ein Sandkorn als Kugel modellieren, kann sein die Oberfläche eines Sandkorns ($s_a$) basierend auf der Volumen eines Schlickkorns ($r_a$) wie folgt berechnet werden:
| $ s_a = 4 \pi r_a ^2 $ |
ID:(3167, 0)
Oberfläche eines Schluffkorns
Gleichung
Da wir ein Schlickkorn als Würfel modellieren, kann sein die Oberfläche eines Schluffkorns ($s_i$) basierend auf der Schlickkornseite ($a_i$) wie folgt berechnet werden:
| $ s_i = 6 a_i ^2 $ |
ID:(3169, 0)
Oberfläche eines Tonkorns
Gleichung
Da wir ein Tonkorn als rechteckigen Quader modellieren, kann sein die Oberfläche eines Tonkorns ($s_c$) basierend auf dem der Länge und Breite eines Tonplättchens ($l_c$) und dem die Höhe eines Tonplättchens ($w_c$) des Tonkorns wie folgt berechnet werden:
| $ s_c = 2 l_c ^2 + 4 w_c l_c $ |
ID:(4361, 0)
Oberfläche von Sandkörnern
Gleichung
Die Oberfläche von Sandkörnern ($S_a$) kann aus der Anzahl der Sandkörner in der Probe ($N_a$) und die Oberfläche eines Sandkorns ($s_a$) wie folgt berechnet werden:
| $ S_a = N_a s_a $ |
ID:(929, 0)
Oberfläche von Schluffkörnern
Gleichung
Die Schlickkornoberfläche ($S_i$) kann aus der Anzahl der Schluffkörner in der Probe ($N_i$) und die Oberfläche eines Schluffkorns ($s_i$) wie folgt berechnet werden:
| $ S_i = N_i s_i $ |
ID:(33, 0)
Oberfläche aus Tonkörnern
Gleichung
Die Tonkornoberfläche ($S_c$), die aus der Anzahl der Tonkörner in der Probe ($N_c$) und die Oberfläche eines Schluffkorns ($s_i$) wie folgt berechnet werden kann:
| $ S_c = N_c s_c $ |
ID:(35, 0)
Inneren Oberfläche des Bodens
Gleichung
Da Körner nur kleinere Bereiche haben, die in Kontakt stehen, können wir in einer ersten Annäherung annehmen, dass ihre gesamte Oberfläche für die Aufnahme von Wasser und die Unterstützung des Lebens zur Verfügung steht. Daher führen wir das Konzept der "inneren Bodenoberfläche" ein und beschreiben es als die Summe aller Kornoberflächen. Auf diese Weise wird die Boden innen Fläche ($S_t$) als Summe von die Oberfläche von Sandkörnern ($S_a$), die Schlickkornoberfläche ($S_i$) und
| $ S_t = S_a + S_l + S_c $ |
ID:(3166, 0)
Innere Oberfläche pro Masse
Gleichung
Das Problem mit die Boden innen Fläche ($S_t$) besteht darin, dass es von der Probengröße abhängt und daher keinen Indikator für die Oberflächenkapazität des Bodens liefert.
Eine Alternative besteht darin, den Wert die Boden innen Fläche ($S_t$) mit die Gesamtmasse ($M_t$) zu normieren, was den Indikator die Innenfläche von Massen ($\gamma_M$) ergibt:
| $ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$ |
ID:(4718, 0)
Innere Oberfläche nach Volumen
Gleichung
Das Problem mit die Boden innen Fläche ($S_t$) besteht darin, dass es von der Probengröße abhängt und daher keinen Indikator für die Oberflächenkapazität des Bodens liefert.
Eine Alternative besteht darin, den Wert von die Boden innen Fläche ($S_t$) mit das Gesamtvolumen ($V_t$) zu normieren, was den Indikator die Innenfläche von Volume ($\gamma_V$) ergibt:
| $ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$ |
ID:(4717, 0)
Massenporosität
Gleichung
Die Massenporosität ($\Phi$) wird ursprünglich auf die gleiche Weise wie die Porosität ($f$) definiert, wird jedoch basierend auf die Trockenschüttdichte ($\rho_b$) und die Teilchendichte ($\rho_p$) geschätzt durch:
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
Die Definition von die Porosität ($f$) erfolgt mit das Solides Volumen ($V_s$) und das Gesamtvolumen ($V_t$), die mit die Gesamttrockenmasse der Probe ($M_s$) modifiziert werden können, sowie mit der Definition:
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
was zu führt:
$\Phi=1-\displaystyle\frac{V_s}{V_t}=1-\displaystyle\frac{V_s}{M_s}\displaystyle\frac{M_s}{V_t}=\displaystyle\frac{V_s}{M_s}\rho_b$
Obwohl die Beziehung zwischen die Gesamttrockenmasse der Probe ($M_s$) und das Solides Volumen ($V_s$) zu die Festkörperdichte ($\rho_s$) gehört, kann diese Dichte mit die Teilchendichte ($\rho_p$) geschätzt werden, was zu führt
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
ID:(15128, 0)
Massensättigungsgrad
Gleichung
Der Relative Massensättigung ($\theta_S$) wird ursprünglich auf die gleiche Weise wie die Relative Sättigung ($\theta_s$) definiert, indem Volumina verwendet werden. Stattdessen kann jedoch anstelle von die Porosität ($f$) Die Massenporosität ($\Phi$) verwendet werden, was zu einem massenbasierten Sättigungsgrad führt:
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
Die Relative Sättigung ($\theta_s$) wird unter Verwendung von der Water Volume ($V_w$) und der Gasvolumen ($V_g$) berechnet durch
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
Wie bei die Porosität ($f$) und das Gesamtvolumen ($V_t$) gilt,
$V_w + V_g = f V_t$
und da die Beziehung Volumen Wasser Land ($\theta_V$) ist
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
dann
$\theta_s=\displaystyle\frac{V_w}{V_w+V_g}=\displaystyle\frac{V_w}{fV_t}=\displaystyle\frac{\theta_V}{f}$
Wenn die Porosität ($f$) mit dem Volumen geschätzt wird und durch die mit der Masse geschätzte die Massenporosität ($\Phi$) ersetzt wird, erhalten wir
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
ID:(15129, 0)