Utilizador: 
Indicadores
Storyboard 
A presença de poros é um dos aspectos fundamentais no comportamento do solo. Por um lado, permite o movimento da água e/ou umidade dentro do solo, mas, por outro lado, afeta as propriedades mecânicas do solo.
Portanto, é crucial contar com indicadores que descrevam a presença de porosidade e a proporção de água que eles contêm, pois esses indicadores desempenham um papel fundamental na caracterização das propriedades hidráulicas, termodinâmicas e mecânicas do solo.
ID:(365, 0)
Modelo de volume sólido, água e gás
Conceito
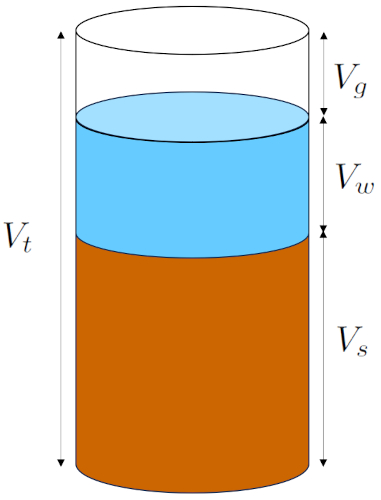
No modelo do solo, o volume total ($V_t$) da amostra é composto por três componentes principais:
• o volume sólido ($V_s$): Essa componente inclui o volume de todos os grãos presentes na amostra.
• o volume de água ($V_w$): Representa o volume da água contida tanto nos microporos quanto nos macroporos do solo.
• o volume de gás ($V_g$): Compreende o volume de gás ou ar contido na amostra.
O diagrama a seguir resume essa descrição:
ID:(1642, 0)
Representação da profundidade efetiva
Imagem
La profundidade efetiva ($D_e$) refere-se à profundidade que a água contida em um volume de solo atingiria se todo o volume sólido fosse "removido", como ilustrado na seguinte imagem:
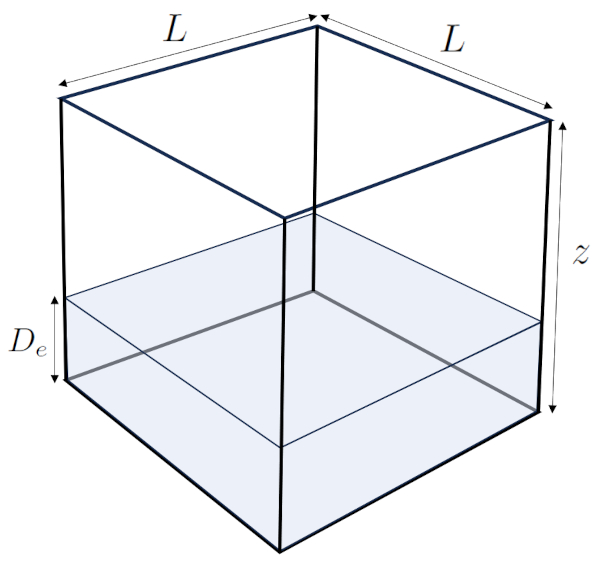
Isso fornece uma medida intuitiva do teor de água no solo.
ID:(1641, 0)
Modelo de massa sólida, água e gás
Conceito
No modelo do solo, la massa total ($M_t$) da amostra é composto por três partes principais:
• la massa seca total da amostra ($M_s$): Este componente inclui as massas de todos os grãos presentes na amostra.
• la massa de água no solo ($M_w$): Representa a massa da água contida tanto nos microporos quanto nos macroporos do solo.
• la massa de gás no solo ($M_g$): Compreende a massa do gás ou ar contido na amostra (que pode ser considerada comparativamente como sendo quase zero, ou seja, $M_g\sim 0$).
ID:(2084, 0)
Superfície interna
Conceito
Uma das propriedades distintivas do material particulado, como o solo, é a sua superfície interna. Por superfície interna, entendemos a soma de todas as superfícies de cada um dos grãos. Esta superfície é um dos fatores-chave para estudar o comportamento da umidade e a presença de nutrientes no solo.
Ao multiplicarmos a superfície de cada grão pela sua quantidade, obtemos a superfície total. Para determinar a superfície de cada grão, é essencial considerar a sua forma. É importante lembrar que tanto a areia quanto o silte são modelados como esferas, enquanto a argila é representada como um paralelepípedo reto.
ID:(1540, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ D_e = \theta_V z $
D_e = theta_V * z
$ e =\displaystyle\frac{ V_g + V_w }{ V_s }$
e =( V_g + V_w )/ V_s
$ f_g =\displaystyle\frac{ V_g }{ V_t }$
f_g = V_g / V_t
$ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$
g_M = S_t / M_s
$ M_t = M_s + M_w $
M_t = M_s + M_w
$ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$
Phi = 1 - rho_b / rho_p
$ \rho_b =\displaystyle\frac{ M_s }{ V_t }$
rho_b = M_s / V_t
$ \rho_w =\displaystyle\frac{ M_w }{ V_w }$
rho_w = M_w / V_w
$ S = \displaystyle\frac{ \theta_V }{ \Phi }$
S = theta_V / Phi
$ S_a = N_a s_a $
S_a = N_a * s_a
$ s_c = 2 l_c ^2 + 4 w_c l_c $
s_c = 2* l_c ^2 + 4* w_c * l_c
$ S_c = N_c s_c $
S_c = N_c * s_c
$ s_i = 6 a_i ^2 $
s_i = 6* a_i ^2
$ S_i = N_i s_i $
S_i = N_i * s_i
$ S_t = S_a + S_l + S_c $
S_t = S_a + S_l + S_c
$ \theta_r =\displaystyle\frac{ V_w }{ V_s }$
theta_r = V_w / V_s
$ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$
theta_s = V_w /( V_g + V_w )
$ \theta_V =\displaystyle\frac{ V_w }{ V_t }$
theta_V = V_w / V_t
$ \theta_w =\displaystyle\frac{ M_w }{ M_s }$
theta_w = M_w / M_s
$ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$
V_g = S_t / V_t
$ V_p = V_w + V_g $
V_p = V_w + V_g
$ V_t = V_s + V_w + V_g $
V_t = V_s + V_w + V_g
$ s_a = 4 \pi r_a ^2 $
s_k = 4* pi * r_a ^2
ID:(15219, 0)
Volume total com água
Equação
O volume total ($V_t$) é obtido somando a parte sólida dos grãos, que corresponde a o volume sólido ($V_s$), à água incluída no o volume de água ($V_w$) e ao ar ou, em geral, ao gás contido no o volume de gás ($V_g$):
| $ V_t = V_s + V_w + V_g $ |
ID:(15089, 0)
Volume de poro
Equação
O volume de poro ($V_p$) não necessariamente está vazio; ele pode conter água, em particular, então introduzimos a variável o volume de água ($V_w$). Por outro lado, o volume restante é considerado como o volume de gás ($V_g$).
Dessa forma, o o volume de poro ($V_p$) é calculado como a soma de ambos os tipos de volumes:
| $ V_p = V_w + V_g $ |
ID:(4723, 0)
Razão volumétrica de água no solo
Equação
Um indicador que aponta a proporção de água dentro do volume total da amostra é La razão volumétrica de água no solo ($\theta_V$). Este é calculado estimando a relação entre o volume de água ($V_w$) e o volume total ($V_t$):
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
ID:(4721, 0)
Razão volumétrica de água sólida
Equação
Um indicador que indica a proporção de água dentro do volume sólido da amostra é La propriedade de porosidade da argila ($\theta_r$). Ele é calculado estimando a relação entre o volume de água ($V_w$) e o volume sólido ($V_s$):
| $ \theta_r =\displaystyle\frac{ V_w }{ V_s }$ |
ID:(4722, 0)
Void ratio
Equação
A relação entre o volume de água e o volume sólido compara a quantidade de água com a quantidade de sólidos no solo. No entanto, uma vez que o volume de água pode variar, é interessante comparar o volume de poro ($V_p$), ou alternativamente a soma de o volume de gás ($V_g$) e o volume de água ($V_w$), com o volume sólido ($V_s$) para definir o indicador la void ratio ($e$) da seguinte forma:
| $ e =\displaystyle\frac{ V_g + V_w }{ V_s }$ |
ID:(4728, 0)
Porosidade do ar
Equação
La porosidade ($f$) é definida como a relação entre o volume de poro ($V_p$) e o volume total ($V_t$). Da mesma forma, la porosidade do ar ($f_g$) é definida com base no volume não ocupado pela água, ou seja, como a relação entre o volume de gás ($V_g$) e o volume total ($V_t$):
| $ f_g =\displaystyle\frac{ V_g }{ V_t }$ |
ID:(4724, 0)
Saturação relativa
Equação
La saturação relativa ($\theta_s$) é calculada como a proporção da porosidade ocupada pela água, definida por o volume de água ($V_w$), dividida pela soma de o volume de água ($V_w$) e o volume de gás ($V_g$), expressa por:
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
ID:(4727, 0)
Profundidade efetiva
Equação
La razão volumétrica de água no solo ($\theta_V$) nos permite estimar a profundidade que a água alcançaria se o solo fosse removido até uma profundidade de la profundidade ($z$), o que é calculado usando a seguinte equação:
| $ D_e = \theta_V z $ |
Se você tem um volume de solo com largura e comprimento $L$ e la profundidade ($z$), seu volume é representado pela seguinte equação:
$V_t = L^2z$
Com la profundidade efetiva ($D_e$) representando uma variável importante, o volume de água pode ser calculado da seguinte maneira:
$V_w = L^2D_e$
Além disso, com a equação
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
podemos relacionar essas variáveis da seguinte forma:
$\theta_V = \displaystyle\frac{V_w}{V_t} = \displaystyle\frac{D_e}{z}$
Portanto, a variável la profundidade efetiva ($D_e$) pode ser calculada usando a seguinte expressão:
| $ D_e = \theta_V z $ |
ID:(3231, 0)
Massa total
Equação
La massa total ($M_t$) é calculada somando la massa seca total da amostra ($M_s$) e la massa de água no solo ($M_w$), da seguinte maneira:
| $ M_t = M_s + M_w $ |
ID:(4247, 0)
Densidade aparente
Equação
Em geral, a densidade é definida como a relação entre a massa e o volume de um material. No caso do solo, que contém porosidade, ao utilizar o volume total ($V_t$), incluem-se o volume sólido ($V_s$), o volume de água ($V_w$) e o volume de poro ($V_p$). Normalmente, a densidade aparente é calculada para o material seco, ou seja, sem água ($M_w \sim 0$), de modo que a la massa total ($M_t$) seja igual à La massa seca total da amostra ($M_s$):
$M_t\sim M_s$
É importante notar que isso é uma aproximação, já que ao secar o solo, sempre fica uma pequena quantidade de água, tornando muito difícil medir com precisão a massa sólida sem água.
Portanto, definimos la densidade aparente seca ($\rho_b$) como a relação entre la massa de água no solo ($M_w$) e o volume total ($V_t$):
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
ID:(4719, 0)
Densidade da água
Equação
Ao trabalhar com água, também é essencial considerar a variável la densidade da água ($\rho_w$), que é calculada usando la massa de água no solo ($M_w$) e o volume de água ($V_w$) com a seguinte equação:
| $ \rho_w =\displaystyle\frac{ M_w }{ V_w }$ |
ID:(4730, 0)
Razão gravimétrica água-sólido
Equação
Se desejarmos indicar em que medida o solo contém água, podemos introduzir um indicador chamado la propriedade de porosidade da argila ($\theta_w$), que é calculado como a relação entre la massa de água no solo ($M_w$) e la massa seca total da amostra ($M_s$), utilizando a seguinte equação:
| $ \theta_w =\displaystyle\frac{ M_w }{ M_s }$ |
ID:(4720, 0)
Superfície de um grão de areia
Equação
Uma vez que modelamos um grão de areia como uma esfera, seu la superfície de um grão de areia ($s_a$) pode ser calculado com base no o raio do grão de areia ($r_a$) da seguinte forma:
| $ s_a = 4 \pi r_a ^2 $ |
ID:(3167, 0)
Superfície de um grão de lodo
Equação
Uma vez que modelamos um grão de silte como um cubo, seu la superfície de um grão de lodo ($s_i$) pode ser calculado com base no o lado de grão de lodo ($a_i$) da seguinte forma:
| $ s_i = 6 a_i ^2 $ |
ID:(3169, 0)
Superfície de um grão de argila
Equação
Uma vez que modelamos um grão de argila como um paralelepípedo retangular, seu la superfície de um grão de argila ($s_c$) pode ser calculado com base no o comprimento e largura de uma placa de argila ($l_c$) e no la altura de um prato de barro ($w_c$) do grão de argila da seguinte forma:
| $ s_c = 2 l_c ^2 + 4 w_c l_c $ |
ID:(4361, 0)
Superfície de grãos de areia
Equação
La superfície de grãos de areia ($S_a$) pode ser calculada a partir o número de grãos de areia na amostra ($N_a$) e la superfície de um grão de areia ($s_a$) da seguinte forma:
| $ S_a = N_a s_a $ |
ID:(929, 0)
Superfície de grãos de lodo
Equação
La superfície de grão de lodo ($S_i$) pode ser calculada a partir o número de grãos de lodo na amostra ($N_i$) e la superfície de um grão de lodo ($s_i$) da seguinte forma:
| $ S_i = N_i s_i $ |
ID:(33, 0)
Superfície de grãos de argila
Equação
La surface de grain d'argile ($S_c$), que pode ser calculada a partir o número de grãos de argila na amostra ($N_c$) e la superfície de um grão de lodo ($s_i$) da seguinte maneira:
| $ S_c = N_c s_c $ |
ID:(35, 0)
Superfície interna do solo
Equação
Dado que os grãos têm apenas seções menores em contato, podemos assumir, em uma primeira aproximação, que toda a sua superfície está disponível para absorver água e suportar a vida. Portanto, introduzimos o conceito de "superfície interior do solo" e a descrevemos como a soma de todas as superfícies dos grãos. Dessa forma, se la superfície interna do solo ($S_t$) é obtida como a soma de la superfície de grãos de areia ($S_a$), la superfície de grão de lodo ($S_i$) e
| $ S_t = S_a + S_l + S_c $ |
ID:(3166, 0)
Área de superfície interna por massa
Equação
O problema com a la superfície interna do solo ($S_t$) é que ela depende do tamanho da amostra e, portanto, não fornece um indicador da capacidade de superfície do solo.
Uma alternativa é normalizar o valor la superfície interna do solo ($S_t$) com la massa total ($M_t$), resultando no indicador la superfície de um grão de lodo ($\gamma_M$):
| $ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$ |
ID:(4718, 0)
Área de superfície interna por volume
Equação
O problema com la superfície interna do solo ($S_t$) é que ela depende do tamanho da amostra e, portanto, não fornece um indicador da capacidade de superfície do solo.
Uma alternativa é normalizar o valor la superfície interna do solo ($S_t$) usando o volume total ($V_t$), resultando no indicador la área de superfície interna por volume ($\gamma_V$):
| $ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$ |
ID:(4717, 0)
Porosidade em massa
Equação
La porosidade em massa ($\Phi$) é inicialmente definido da mesma forma que la porosidade ($f$), no entanto, é estimado com base em la densidade aparente seca ($\rho_b$) e la densidade de partículas ($\rho_p$) da seguinte forma:
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
A definição de la porosidade ($f$) é feita com o volume sólido ($V_s$) e o volume total ($V_t$), que podem ser modificados com la massa seca total da amostra ($M_s$) e a definição:
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
resultando em:
$\Phi=1-\displaystyle\frac{V_s}{V_t}=1-\displaystyle\frac{V_s}{M_s}\displaystyle\frac{M_s}{V_t}=\displaystyle\frac{V_s}{M_s}\rho_b$
Embora a relação entre la massa seca total da amostra ($M_s$) e o volume sólido ($V_s$) corresponda a la densidade sólida ($\rho_s$), essa densidade pode ser estimada usando la densidade de partículas ($\rho_p$), levando a
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
ID:(15128, 0)
Grau de saturação de massa
Equação
O saturação de massa relativa ($\theta_S$) é inicialmente definido da mesma forma que la saturação relativa ($\theta_s$), utilizando volumes. No entanto, em vez de usar la porosidade ($f$), você pode usar la porosidade em massa ($\Phi$) em seu lugar, resultando em um grau de saturação baseado na massa:
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
La saturação relativa ($\theta_s$) é calculado usando o volume de água ($V_w$) e o volume de gás ($V_g$) da seguinte forma:
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
Assim como com la porosidade ($f$) e o volume total ($V_t$),
$V_w + V_g = f V_t$
e como la razão volumétrica de água no solo ($\theta_V$) é
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
então
$\theta_s=\displaystyle\frac{V_w}{V_w+V_g}=\displaystyle\frac{V_w}{fV_t}=\displaystyle\frac{\theta_V}{f}$
Se la porosidade ($f$) for estimado usando o volume e substituído pelo estimado com a massa la porosidade em massa ($\Phi$), obtemos
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
ID:(15129, 0)