User:
Indicators
Storyboard 
The presence of pores is one of the key aspects of soil behavior. On one hand, it enables the movement of water and/or moisture within the soil, but on the other hand, it affects the soil's mechanical properties.
Therefore, it is crucial to have indicators that describe the presence of porosity and the proportion of water they contain, as these indicators play a vital role in characterizing the hydraulic, thermodynamic, and mechanical properties of the soil.
ID:(365, 0)
Model of solid volume, water and gas
Concept
In the soil model, the total volume ($V_t$) of the sample consists of three main components:
• the solid volume ($V_s$): This component includes the volume of all the grains present in the sample.
• the water Volume ($V_w$): Represents the volume of water contained in both the micropores and macropores of the soil.
• the gas Volume ($V_g$): Comprises the volume of gas or air contained in the sample.
The following diagram summarizes this description:
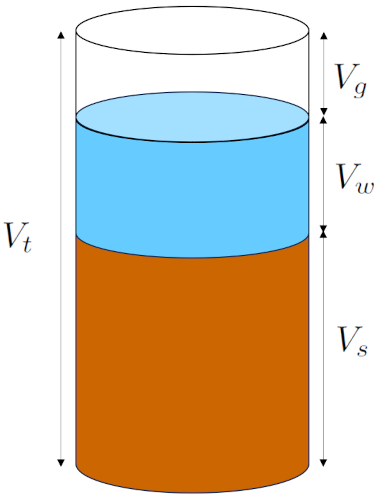
None
ID:(1642, 0)
Representation of effective depth
Image
The effective Depth ($D_e$) refers to the depth that the water contained in a volume of soil would reach if all the solid volume were "removed," as illustrated in the following image:
None
This provides an intuitive measure of the water content in the soil.
ID:(1641, 0)
Mass model of solid, water and gas
Concept
In the soil model, the total Mass ($M_t$) of the sample consists of three main components:
• the total Dry Mass of Sample ($M_s$): This component includes the masses of all the grains present in the sample.
• the mass of water in the soil ($M_w$): Represents the mass of water contained in both the micropores and macropores of the soil.
• the mass of gas in the soil ($M_g$): Comprises the mass of gas or air contained in the sample (which can be comparatively considered as nearly zero, i.e., $M_g\sim 0$).
ID:(2084, 0)
Internal surface
Concept
One of the distinguishing properties of particulate matter, such as soil, is its internal surface area. By internal surface area, we mean the sum of all the surfaces of each of the grains. This surface area is one of the key factors for studying moisture behavior and the presence of nutrients in the soil.
When we multiply the surface area of each grain by its quantity, we obtain the total surface area. To determine the surface area of each grain, it is essential to consider its shape. It's important to remember that both sand and silt are modeled as spheres, while clay is represented as a straight parallelepiped.
ID:(1540, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ D_e = \theta_V z $
D_e = theta_V * z
$ e =\displaystyle\frac{ V_g + V_w }{ V_s }$
e =( V_g + V_w )/ V_s
$ f_g =\displaystyle\frac{ V_g }{ V_t }$
f_g = V_g / V_t
$ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$
g_M = S_t / M_s
$ M_t = M_s + M_w $
M_t = M_s + M_w
$ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$
Phi = 1 - rho_b / rho_p
$ \rho_b =\displaystyle\frac{ M_s }{ V_t }$
rho_b = M_s / V_t
$ \rho_w =\displaystyle\frac{ M_w }{ V_w }$
rho_w = M_w / V_w
$ S = \displaystyle\frac{ \theta_V }{ \Phi }$
S = theta_V / Phi
$ S_a = N_a s_a $
S_a = N_a * s_a
$ s_c = 2 l_c ^2 + 4 w_c l_c $
s_c = 2* l_c ^2 + 4* w_c * l_c
$ S_c = N_c s_c $
S_c = N_c * s_c
$ s_i = 6 a_i ^2 $
s_i = 6* a_i ^2
$ S_i = N_i s_i $
S_i = N_i * s_i
$ S_t = S_a + S_l + S_c $
S_t = S_a + S_l + S_c
$ \theta_r =\displaystyle\frac{ V_w }{ V_s }$
theta_r = V_w / V_s
$ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$
theta_s = V_w /( V_g + V_w )
$ \theta_V =\displaystyle\frac{ V_w }{ V_t }$
theta_V = V_w / V_t
$ \theta_w =\displaystyle\frac{ M_w }{ M_s }$
theta_w = M_w / M_s
$ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$
V_g = S_t / V_t
$ V_p = V_w + V_g $
V_p = V_w + V_g
$ V_t = V_s + V_w + V_g $
V_t = V_s + V_w + V_g
$ s_a = 4 \pi r_a ^2 $
s_k = 4* pi * r_a ^2
ID:(15219, 0)
Total volume with water
Equation
The total volume ($V_t$) is obtained by adding the solid part of the grains, which corresponds to the solid volume ($V_s$), to the water included in the water Volume ($V_w$), and the air or, in general, the gas contained in the gas Volume ($V_g$):
| $ V_t = V_s + V_w + V_g $ |
ID:(15089, 0)
Pore volume
Equation
The pore volume ($V_p$) is not necessarily empty; it can contain water, in particular, so we introduce the variable the water Volume ($V_w$). On the other hand, the remaining volume is considered as the gas Volume ($V_g$).
In this way, the pore volume ($V_p$) is calculated as the sum of both types of volumes:
| $ V_p = V_w + V_g $ |
ID:(4723, 0)
Soil water volumetric ratio
Equation
An indicator that indicates the proportion of water within the total volume of the sample is the relationship volumetric water land ($\theta_V$). It is calculated by estimating the ratio between the water Volume ($V_w$) and the total volume ($V_t$):
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
ID:(4721, 0)
Solid water volumetric ratio
Equation
An indicator that signifies the proportion of water within the solid volume of the sample is the relationship volumetric water solido ($\theta_r$). It is calculated by estimating the ratio between the water Volume ($V_w$) and the solid volume ($V_s$):
| $ \theta_r =\displaystyle\frac{ V_w }{ V_s }$ |
ID:(4722, 0)
Void ratio
Equation
The relationship between the volume of water and the solid volume compares the amount of water to the amount of solids in the soil. However, since the volume of water can vary, it is interesting to compare the pore volume ($V_p$), or alternatively the sum of the gas Volume ($V_g$) and the water Volume ($V_w$), with the solid volume ($V_s$) to define the void ratio ($e$) as follows:
| $ e =\displaystyle\frac{ V_g + V_w }{ V_s }$ |
ID:(4728, 0)
Air porosity
Equation
The porosity ($f$) is defined as the relationship between the pore volume ($V_p$) and the total volume ($V_t$). Similarly, the air Porosity ($f_g$) is defined based on the volume not occupied by water, which is the relationship between the gas Volume ($V_g$) and the total volume ($V_t$):
| $ f_g =\displaystyle\frac{ V_g }{ V_t }$ |
ID:(4724, 0)
Relative saturation
Equation
The relative Saturation ($\theta_s$) is calculated as the proportion of porosity occupied by water, defined by the water Volume ($V_w$), divided by the sum of the water Volume ($V_w$) and the gas Volume ($V_g$), expressed as:
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
ID:(4727, 0)
Effective Depth
Equation
The relationship volumetric water land ($\theta_V$) allows us to estimate the effective Depth ($D_e$) that the water would reach if the soil were removed to a depth of the depth ($z$), which is calculated using the following equation:
| $ D_e = \theta_V z $ |
If you have a volume of soil with width and length $L$ and the depth ($z$), its volume is represented by the equation:
$V_t = L^2z$
With the effective Depth ($D_e$) representing an important variable, the volume of water can be calculated as follows:
$V_w = L^2D_e$
Furthermore, with the equation
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
we can relate these variables as follows:
$\theta_V = \displaystyle\frac{V_w}{V_t} = \displaystyle\frac{D_e}{z}$
Therefore, the variable the effective Depth ($D_e$) can be calculated using the following expression:
| $ D_e = \theta_V z $ |
ID:(3231, 0)
Total Mass
Equation
The total Mass ($M_t$) is calculated by adding the total Dry Mass of Sample ($M_s$) and the mass of water in the soil ($M_w$) together, as follows:
| $ M_t = M_s + M_w $ |
ID:(4247, 0)
Apparent density
Equation
In general, density is defined as the ratio of mass to volume of a material. In the case of soil, which contains porosity, when using the total volume ($V_t$), it includes the solid volume ($V_s$), the water Volume ($V_w$), and the pore volume ($V_p$). Typically, apparent density is calculated for dry material, i.e., without water ($M_w \sim 0$), so that the total Mass ($M_t$) is equal to the total Dry Mass of Sample ($M_s$):
$M_t\sim M_s$
It's important to note that this is an approximation, as when soil is dried, a small amount of water always remains, making it very difficult to accurately measure the solid mass without water.
Therefore, we define the dry bulk density ($\rho_b$) as the ratio of the mass of water in the soil ($M_w$) to the total volume ($V_t$):
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
ID:(4719, 0)
Water density
Equation
When working with water, it's also crucial to consider the variable the water density ($\rho_w$), which is calculated using the mass of water in the soil ($M_w$) and the water Volume ($V_w$) with the following equation:
| $ \rho_w =\displaystyle\frac{ M_w }{ V_w }$ |
ID:(4730, 0)
Gravimetric water-solid ratio
Equation
If we wish to indicate the extent to which the soil contains water, we can introduce an indicator called the relationship gravimetric water solido ($\theta_w$), which is calculated as the ratio of the mass of water in the soil ($M_w$) to the total Dry Mass of Sample ($M_s$), using the following equation:
| $ \theta_w =\displaystyle\frac{ M_w }{ M_s }$ |
ID:(4720, 0)
Surface of a grain of sand
Equation
Since we model a grain of sand as a sphere, its the surface of a grain of sand ($s_a$) can be calculated based on the sand grain radius ($r_a$) as follows:
| $ s_a = 4 \pi r_a ^2 $ |
ID:(3167, 0)
Surface of a silt grain
Equation
Since we model a grain of silt as a cube, its the surface of a silt grain ($s_i$) can be calculated based on the silt Grain Side ($a_i$) as follows:
| $ s_i = 6 a_i ^2 $ |
ID:(3169, 0)
Surface of a grain of clay
Equation
Since we model a clay grain as a rectangular parallelepiped, its the surface of a grain of clay ($s_c$) can be calculated based on the the length and width of a clay plate ($l_c$) and the height of a clay plate ($w_c$) of the clay grain as follows:
| $ s_c = 2 l_c ^2 + 4 w_c l_c $ |
ID:(4361, 0)
Surface of sand grains
Equation
The surface of sand grains ($S_a$) can be calculated from the number of sand grains in the sample ($N_a$) and the surface of a grain of sand ($s_a$) as follows:
| $ S_a = N_a s_a $ |
ID:(929, 0)
Surface of silt grains
Equation
The silt grain surface ($S_i$) can be calculated from the number of silt grains in the sample ($N_i$) and the surface of a silt grain ($s_i$) as follows:
| $ S_i = N_i s_i $ |
ID:(33, 0)
Surface of clay grains
Equation
The clay grain surface ($S_c$), which can be calculated from the number of clay grains in the sample ($N_c$) and the surface of a silt grain ($s_i$) as follows:
| $ S_c = N_c s_c $ |
ID:(35, 0)
Inner Surface of the Soil
Equation
Since grains only have smaller sections in contact, we can assume, in a first approximation, that their entire surface is available for absorbing water and supporting life. Therefore, we introduce the concept of the "interior soil surface" and describe it as the sum of all the grain surfaces. In this way, if the soil Inner Surface ($S_t$) is obtained as the sum of the surface of sand grains ($S_a$), the silt grain surface ($S_i$), and
| $ S_t = S_a + S_l + S_c $ |
ID:(3166, 0)
Internal surface area per mass
Equation
The issue with the soil Inner Surface ($S_t$) is that it depends on the sample size and, therefore, does not provide an indicator of the soil's surface capacity.
An alternative is to normalize the the soil Inner Surface ($S_t$) value with the total Mass ($M_t$), resulting in the indicator the inner Surface by Mass ($\gamma_M$):
| $ \gamma_M =\displaystyle\frac{ S_t }{ M_s }$ |
ID:(4718, 0)
Internal surface area by volume
Equation
The issue with the soil Inner Surface ($S_t$) is that it depends on the sample size and, therefore, does not provide an indicator of the soil's surface capacity.
An alternative is to normalize the value of the soil Inner Surface ($S_t$) using the total volume ($V_t$), resulting in the indicator the inner Surface by Volume ($\gamma_V$):
| $ \gamma_V =\displaystyle\frac{ S_t }{ V_t }$ |
ID:(4717, 0)
Mass porosity
Equation
The mass porosity ($\Phi$) is initially defined in the same way as the porosity ($f$), however, it is estimated based on the dry bulk density ($\rho_b$) and the particle density ($\rho_p$) through:
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
The definition of the porosity ($f$) is carried out with the solid volume ($V_s$) and the total volume ($V_t$), which can be modified with the total Dry Mass of Sample ($M_s$) and the definition:
| $ \rho_b =\displaystyle\frac{ M_s }{ V_t }$ |
resulting in:
$\Phi=1-\displaystyle\frac{V_s}{V_t}=1-\displaystyle\frac{V_s}{M_s}\displaystyle\frac{M_s}{V_t}=\displaystyle\frac{V_s}{M_s}\rho_b$
Although the relationship between the total Dry Mass of Sample ($M_s$) and the solid volume ($V_s$) corresponds to the solid Density ($\rho_s$), this density can be estimated using the particle density ($\rho_p$), leading to
| $ \Phi = 1 - \displaystyle\frac{ \rho_b }{ \rho_p }$ |
ID:(15128, 0)
Mass saturation degree
Equation
The relative mass saturation ($\theta_S$) is initially defined in the same way as the relative Saturation ($\theta_s$), using volumes. However, instead of using the porosity ($f$), you can use the mass porosity ($\Phi$) instead, resulting in a mass-based degree of saturation:
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
The relative Saturation ($\theta_s$) is calculated using the water Volume ($V_w$) and the gas Volume ($V_g$) through
| $ \theta_s =\displaystyle\frac{ V_w }{ V_g + V_w }$ |
As with the porosity ($f$) and the total volume ($V_t$),
$V_w + V_g = f V_t$
and since the relationship volumetric water land ($\theta_V$) is
| $ \theta_V =\displaystyle\frac{ V_w }{ V_t }$ |
then
$\theta_s=\displaystyle\frac{V_w}{V_w+V_g}=\displaystyle\frac{V_w}{fV_t}=\displaystyle\frac{\theta_V}{f}$
If the porosity ($f$) is estimated using volume and replaced with the one estimated with mass the mass porosity ($\Phi$), we get
| $ S = \displaystyle\frac{ \theta_V }{ \Phi }$ |
ID:(15129, 0)