Utilizador:
Lençol freático próximo a um corpo de água
Storyboard 
No caso do lençol freático na borda de um corpo de água cujo nível não é afetado pelo seu fluxo (como em uma área costeira ou lacustre), a altura do lençol freático acima desse corpo de água na borda deve ser zero. Assumindo que o solo é homogêneo, o perfil da altura do lençol freático acima do nível da água pode ser calculado, atendendo a essa condição de contorno.
ID:(2083, 0)
Fluxo de chuva em um corpo de água
Conceito
No caso do fluxo em direção a um corpo d'água, o sistema pode ser modelado de forma unidimensional, onde la altura da coluna d'água no solo ($h$) é uma função de la posição da coluna d'água no solo ($x$). Na borda do corpo d'água, o fluxo longitudinal deve ser igual a o fluxo em um ponto de referência ($j_{s0}$) multiplicado por la altura de referência da coluna de água ($h_0$), que deve corresponder ao fluxo gerado pela chuva, ou seja, o taxa de precipitação ($r$) multiplicado por o distância horizontal até o topo ($d$), expresso como:
| $ h_0 j_{s0} = r d $ |
e representado no gráfico:
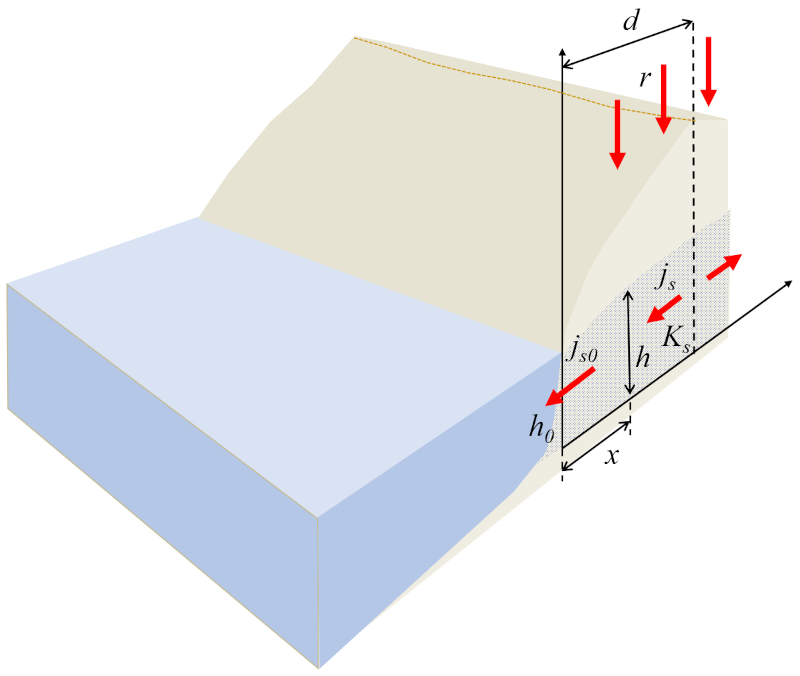
Para o modelamento, assume-se que o solo é homogêneo com uma constante de la condutividade hidráulica ($K_s$) e que o fluxo se desloca da área com a altura máxima do terreno, que está a o distância horizontal até o topo ($d$), em direção ao corpo d'água.
ID:(15831, 0)
Altura de fluxo da solução em um corpo de água
Conceito
A solução da equação unidimensional de fluxo em direção a um corpo d'água, que calcula o valor de la altura da coluna d'água no solo ($h$) em função de la altura de referência da coluna de água ($h_0$) e la posição da coluna d'água no solo ($x$) na borda do corpo d'água, juntamente com o distância horizontal até o topo ($d$) e o fator de precipitação ($\mu_r$), é dada por:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
Essa solução é representada graficamente em função dos fatores adicionais $h/h_0$ e $x/d$ da seguinte maneira:
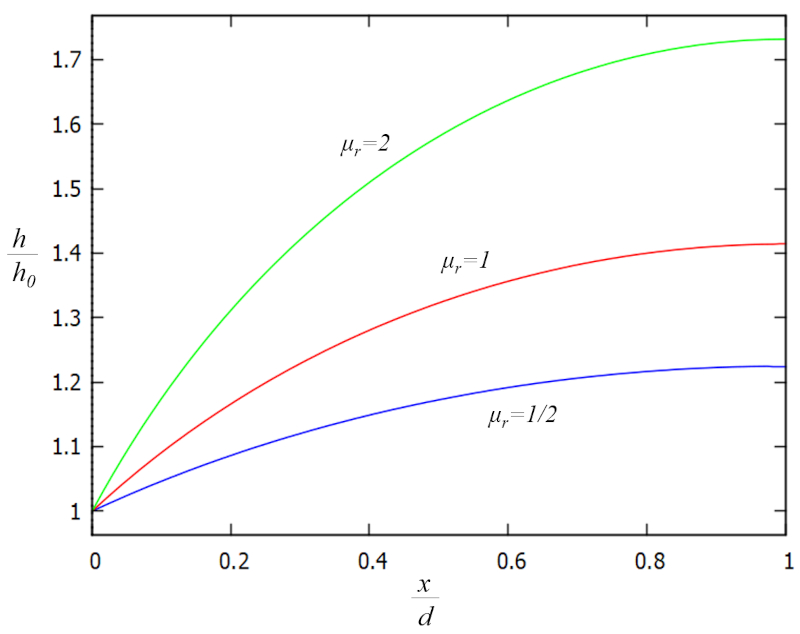
A função depende do fator o fator de precipitação ($\mu_r$), que é especialmente influenciado por o taxa de precipitação ($r$) e o distância horizontal até o topo ($d$), de modo que:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
Isso indica que, se o efeito da chuva com $r d^2$ predomina sobre a capacidade de fluxo de água do solo, representada por $K_s h_0^2$, ocorrerá acumulação de água no solo. Por outro lado, se a expressão $K_s h_0^2$ predomina, o solo tenderá a "esvaziar-se" em direção ao corpo d'água sem retenção significativa.
ID:(15827, 0)
Solução de densidade de fluxo em direção a um corpo de água
Conceito
A solução obtida para a altura e os parâmetros o fluxo em um ponto de referência ($j_{s0}$) e la altura de referência da coluna de água ($h_0$) revela que la densidade de fluxo ($j_s$) é dado por:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Podemos representar graficamente la densidade de fluxo ($j_s$) em função dos fatores adicionais $j_s/j_{s0}$ e $x/s_0$ da seguinte maneira:
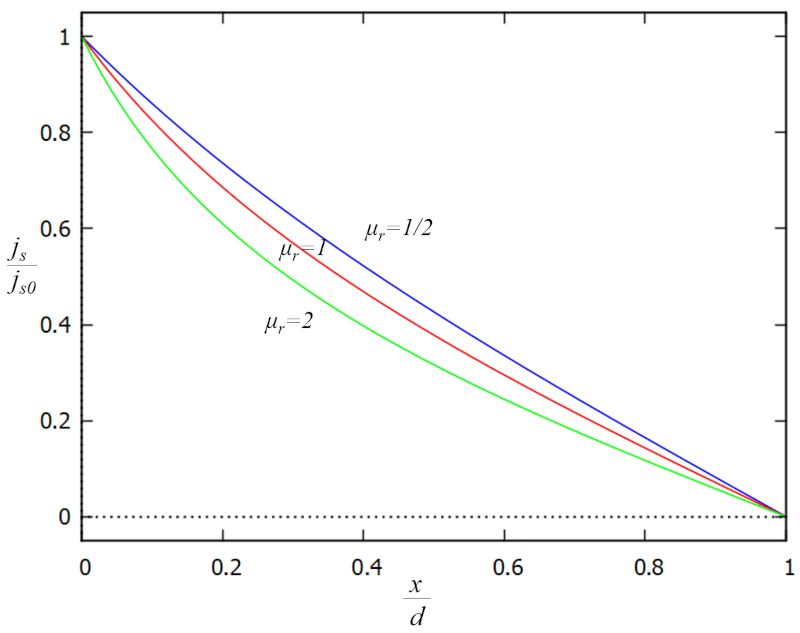
É perceptível que la densidade de fluxo ($j_s$) continua a aumentar à medida que nos aproximamos do canal, à medida que la altura da coluna d'água no solo ($h$) diminui. Esse aumento é necessário para manter a velocidade do fluxo em la densidade de fluxo ($j_s$) ou, alternativamente, para aumentá-la.
ID:(15828, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $
h / h_0 = sqrt(1 + mu_r * x *(2 - x / d )/ d )
$ h_0 j_{s0} = r d $
h_0 * j_s0 = r * d
$\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$
j_s / j_s0 = (1- x / d )/sqrt(1 + mu_r * x *(2- x / d )/ d )
$ j_s = - K_s \displaystyle\frac{ dh }{ dx }$
j_s = - K_s * dh / dx
$ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$
mu_r = r * d ^2/( K_s * h_0 ^2)
$\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $
@DIFF( h * @DIFF( h , x, 1), x ,1) = - r / K_s
$\displaystyle\frac{d}{dx}( h j_s )= r $
@DIFF( h * j_s , x ,1) = r
ID:(15822, 0)
Equilíbrio de fluxo com chuva
Equação
No caso estacionário, a variação de la posição da coluna d'água no solo ($x$) do produto de la altura da coluna d'água no solo ($h$) e la velocidade do fluido ($j_s$) deve ser igual a menos o taxa de precipitação ($r$):
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Se para la altura da coluna d'água no solo ($h$) multiplicado por la densidade de fluxo ($j_s$), a equação para la posição da coluna d'água no solo ($x$) e o tempo ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
no caso estacionário se reduz a
$\displaystyle\frac{d}{dx} (h j_s) = 0$
isso implica que o produto de la altura da coluna d'água no solo ($h$) por la densidade de fluxo ($j_s$) é constante. Em caso de chuva, a água adere a toda a superfície a uma taxa de um taxa de precipitação ($r$):
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Nota: A equação diferencial é uma equação diferencial ordinária, pois depende unicamente de la posição da coluna d'água no solo ($x$) e não de o tempo ($t$).
ID:(15823, 0)
Densidade de fluxo e condutividade hidráulica
Equação
La densidade de fluxo ($j_s$) pode ser expresso em termos de la condutividade hidráulica ($K_s$), la altura da coluna d'água no solo ($h$) e la posição da coluna d'água no solo ($x$) da seguinte maneira:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Dado que la densidade de fluxo ($j_s$) em relação a o raio de um grão genérico ($r_0$), la porosidade própria genérica ($q_0$), la porosidade ($f$), la densidade líquida ($\rho_w$), la aceleração gravitacional ($g$), la viscosidade ($\eta$), la diferença de altura ($\Delta h$) e o comprimento da amostra ($\Delta L$) é representado por
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
e la condutividade hidráulica ($K_s$) é representado por
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
no limite infinitesimal em que la diferença de altura ($\Delta h$) é igual a la diferencial de altura da coluna ($dh$)
$\Delta h \rightarrow dh$
e em que o comprimento da amostra ($\Delta L$) é igual a la diferencial de distância ($dx$)
$\Delta L \rightarrow dx$
isso nos leva a
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
ID:(15226, 0)
Equação de fluxo em um corpo de água
Equação
A equação diferencial para calcular la altura da coluna d'água no solo ($h$) em função de la posição da coluna d'água no solo ($x$), o taxa de precipitação ($r$) e la condutividade hidráulica ($K_s$) é:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
A equação para o produto de la altura da coluna d'água no solo ($h$) e la densidade de fluxo ($j_s$) em função de la posição da coluna d'água no solo ($x$) e o taxa de precipitação ($r$) é a seguinte:
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Com a equação que descreve la densidade de fluxo ($j_s$) em termos de la condutividade hidráulica ($K_s$) e la posição da coluna d'água no solo ($x$):
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
podemos derivar a equação resultante da seguinte maneira:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
ID:(15824, 0)
Fator de precipitação
Equação
O fator de precipitação ($\mu_r$) é definido utilizando o taxa de precipitação ($r$), o distância horizontal até o topo ($d$), la altura de referência da coluna de água ($h_0$) e la condutividade hidráulica ($K_s$) da seguinte maneira:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
ID:(15829, 0)
Altura do fluxo em um corpo de água
Equação
A equação para la altura da coluna d'água no solo ($h$) em função de la altura de referência da coluna de água ($h_0$), la posição da coluna d'água no solo ($x$), o distância horizontal até o topo ($d$) e o fator de precipitação ($\mu_r$) é a seguinte:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
A equação para la altura da coluna d'água no solo ($h$) em função de la posição da coluna d'água no solo ($x$) e que depende de o taxa de precipitação ($r$) e la condutividade hidráulica ($K_s$) é a seguinte:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
Podemos rearranjá-la para facilitar a integração da seguinte forma:
$\displaystyle\frac{d}{dx}\left(h\displaystyle\frac{dh}{dx}\right)=\displaystyle\frac{d}{dx}\displaystyle\frac{1}{2}\displaystyle\frac{d h^2}{dx} = \displaystyle\frac{1}{2}\displaystyle\frac{d^2 h^2}{dx^2}=- \displaystyle\frac{r}{K_s}$
Integrando com as condições de que a profundidade na borda do corpo de água é La altura de referência da coluna de água ($h_0$):
$h(0) = h_0$
e que o fluxo em o distância horizontal até o topo ($d$) é nulo:
$j_s(d) = -K_s\displaystyle\frac{d h}{dx}|_{x=d} = 0$
obtemos com o fator de precipitação ($\mu_r$):
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
que:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
ID:(15825, 0)
Solução estática em uma dimensão
Equação
Podemos estudar o caso estacionário, o que implica que o produto de la altura de referência da coluna de água ($h_0$) por o fluxo em um ponto de referência ($j_{s0}$) deve ser constante e, em particular, deve coincidir com o fluxo de chuva dado por o taxa de precipitação ($r$) e o distância horizontal até o topo ($d$):
| $ h_0 j_{s0} = r d $ |
Se para la altura da coluna d'água no solo ($h$) dividido por la densidade de fluxo ($j_s$), a equação com la posição da coluna d'água no solo ($x$) e o tempo ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
no caso estacionário se reduz a
$\displaystyle\frac{d}{dx} (h j_s) = 0$
isso implica que o produto de la altura de referência da coluna de água ($h_0$) e o fluxo em um ponto de referência ($j_{s0}$) deve ser constante e, em particular, deve coincidir com o fluxo da chuva representado por o taxa de precipitação ($r$) e o distância horizontal até o topo ($d$). Portanto, temos que:
| $ h_0 j_{s0} = r d $ |
Nota: A equação diferencial é uma equação diferencial ordinária, pois depende unicamente de la posição da coluna d'água no solo ($x$) e não de o tempo ($t$).
ID:(15830, 0)
Densidade de fluxo em um corpo de água
Equação
A solução para la densidade de fluxo ($j_s$) e o fluxo em um ponto de referência ($j_{s0}$), dados la posição da coluna d'água no solo ($x$), o distância horizontal até o topo ($d$) e o fator de precipitação ($\mu_r$), é a seguinte:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Com a solução para la altura da coluna d'água no solo ($h$) baseada em la altura de referência da coluna de água ($h_0$), la posição da coluna d'água no solo ($x$), o distância horizontal até o topo ($d$) e o fator de precipitação ($\mu_r$):
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
podemos calcular la densidade de fluxo ($j_s$) utilizando la condutividade hidráulica ($K_s$) com:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
e aplicando o fluxo em um ponto de referência ($j_{s0}$) e o taxa de precipitação ($r$) em:
| $ h_0 j_{s0} = r d $ |
dessa forma, obtemos:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
ID:(15826, 0)