Usuario:
Napa próximo a cuerpo de agua
Storyboard 
En el caso de la napa freática en el borde de un cuerpo de agua cuyo nivel no es afectado por el flujo de la misma (como una zona costera o lacustre), la altura de la napa sobre dicho cuerpo de agua en el borde debe ser nula. Si se asume que el suelo es homogéneo, se puede calcular el perfil de la altura de la napa sobre el nivel del agua cumpliendo con esta condición de borde.
ID:(2083, 0)
Flujo de lluvia hacia un cuerpo de agua
Concepto
En el caso del flujo hacia un cuerpo de agua, se puede modelar el sistema de manera unidimensional, donde la altura de la columna de agua en el suelo ($h$) es una función de la posición de la columna de agua en el suelo ($x$). En el borde del cuerpo de agua, el flujo longitudinal debe ser igual a el flujo en un punto de referencia ($j_{s0}$) por la altura de referencia de la columna de agua ($h_0$), que debe corresponder al flujo generado por la lluvia, es decir, el velocidad de precipitaciones ($r$) por el distancia horizontal hasta la cúspide ($d$), expresado como:
| $ h_0 j_{s0} = r d $ |
y representado en la gráfica:
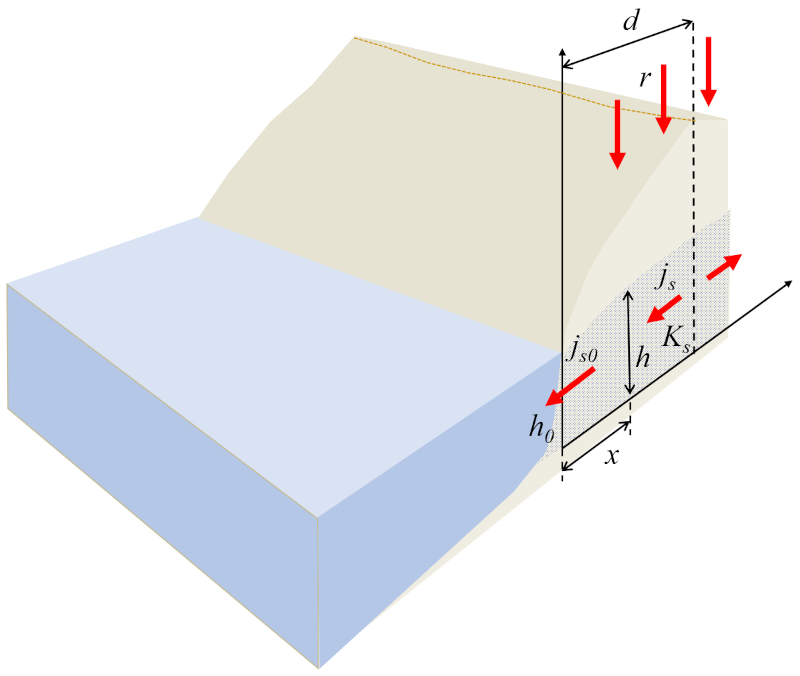
Para el modelado, se asume que el suelo es homogéneo con una la conductividad hidráulica ($K_s$) constante y que el flujo se desplaza desde la zona de máxima altura del terreno, ubicada a el distancia horizontal hasta la cúspide ($d$), hacia el cuerpo de agua.
ID:(15831, 0)
Solución altura del flujo hacia un cuerpo de agua
Concepto
La solución de la ecuación unidimensional de flujo hacia un cuerpo de agua, que calcula el valor de la altura de la columna de agua en el suelo ($h$) en función de la altura de referencia de la columna de agua ($h_0$) y la posición de la columna de agua en el suelo ($x$) en el borde del cuerpo de agua, junto con el distancia horizontal hasta la cúspide ($d$) y el factor de precipitaciones ($\mu_r$), es la siguiente:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
Esta solución se ilustra gráficamente en función de los factores adicionales $h/h_0$ y $x/d$ como se muestra a continuación:
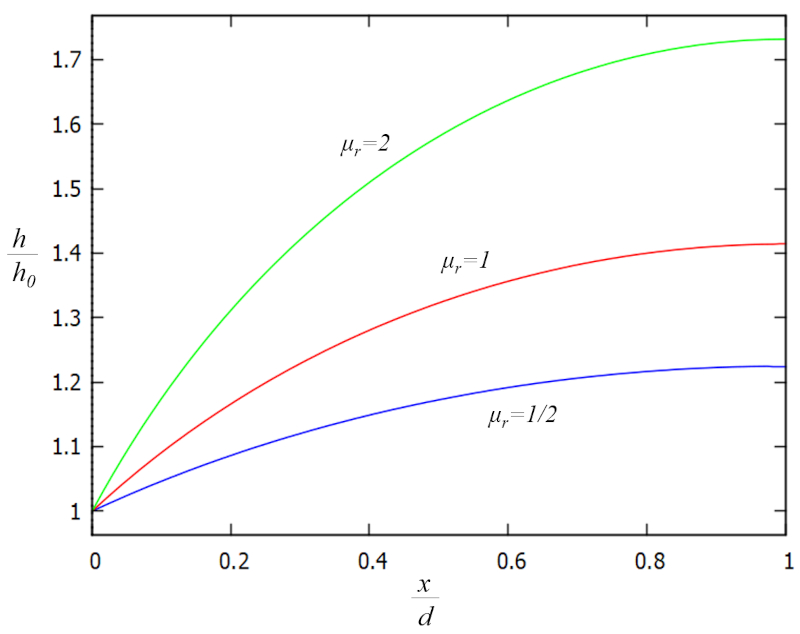
La función depende del factor el factor de precipitaciones ($\mu_r$), que está especialmente influenciado por el velocidad de precipitaciones ($r$) y el distancia horizontal hasta la cúspide ($d$), de modo que:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
Esto sugiere que, si el efecto de la lluvia con $r d^2$ predomina sobre la capacidad de flujo del agua a través del suelo, representada por $K_s h_0^2$, se producirá acumulación de agua en el suelo. Por el contrario, si domina la expresión $K_s h_0^2$, el suelo tenderá a "vaciarse" hacia el cuerpo de agua sin una retención significativa.
ID:(15827, 0)
Solución densidad de flujo hacia un cuerpo de agua
Concepto
La solución para la densidad de flujo ($j_s$) y el flujo en un punto de referencia ($j_{s0}$) dados la posición de la columna de agua en el suelo ($x$), el distancia horizontal hasta la cúspide ($d$) y el factor de precipitaciones ($\mu_r$) es la siguiente:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Podemos representar la densidad de flujo ($j_s$) gráficamente en función de los factores adicionales $j_s/j_{s0}$ y $x/d$ de la siguiente manera:
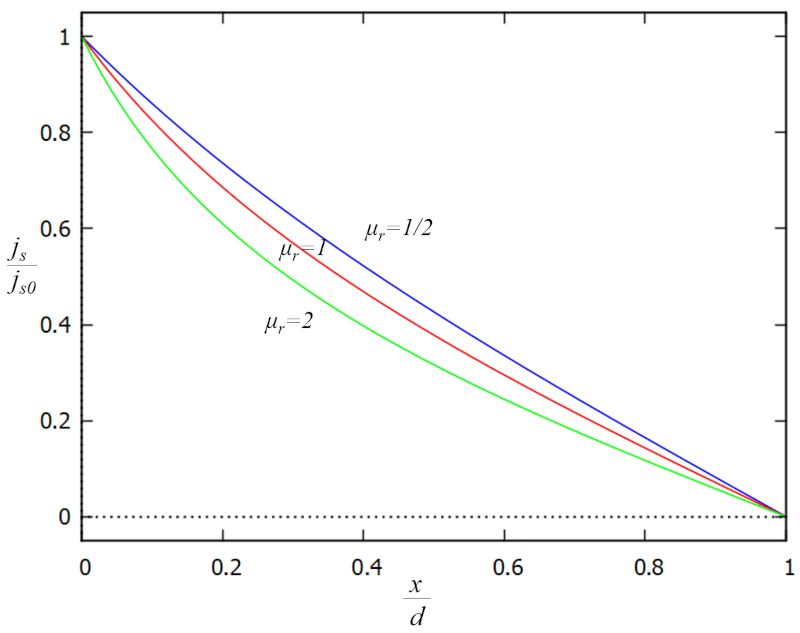
la densidad de flujo ($j_s$) continúa aumentando a medida que nos acercamos al cuerpo de agua, a medida que la altura de la columna de agua en el suelo ($h$) disminuye. Este aumento es necesario para mantener el flujo total constante.
ID:(15828, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $
h / h_0 = sqrt(1 + mu_r * x *(2 - x / d )/ d )
$ h_0 j_{s0} = r d $
h_0 * j_s0 = r * d
$\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$
j_s / j_s0 = (1- x / d )/sqrt(1 + mu_r * x *(2- x / d )/ d )
$ j_s = - K_s \displaystyle\frac{ dh }{ dx }$
j_s = - K_s * dh / dx
$ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$
mu_r = r * d ^2/( K_s * h_0 ^2)
$\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $
@DIFF( h * @DIFF( h , x, 1), x ,1) = - r / K_s
$\displaystyle\frac{d}{dx}( h j_s )= r $
@DIFF( h * j_s , x ,1) = r
ID:(15822, 0)
Balance de flujo con lluvia
Ecuación
En el caso estacionario, la variación de la posición de la columna de agua en el suelo ($x$) del producto de la altura de la columna de agua en el suelo ($h$) y la velocidad del fluido ($j_s$) debe ser igual a menos el velocidad de precipitaciones ($r$):
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Si para la altura de la columna de agua en el suelo ($h$) multiplicado por la densidad de flujo ($j_s$) la ecuación para la posición de la columna de agua en el suelo ($x$) y el tiempo ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
en el caso estacionario se reduce a
$\displaystyle\frac{d}{dx} (h j_s) = 0$
esto implica que el producto de la altura de la columna de agua en el suelo ($h$) por la densidad de flujo ($j_s$) es constante. En caso de lluvia, el agua se adhiere a toda la superficie a una tasa de un velocidad de precipitaciones ($r$):
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Nota: La ecuación diferencial es una ecuación diferencial ordinaria, ya que depende únicamente de la posición de la columna de agua en el suelo ($x$) y no de el tiempo ($t$).
ID:(15823, 0)
Densidad de flujo y conductividad hidráulica
Ecuación
La densidad de flujo ($j_s$) se puede expresar en términos de la conductividad hidráulica ($K_s$), la altura de la columna de agua en el suelo ($h$) y la posición de la columna de agua en el suelo ($x$) de la siguiente manera:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Dado que la densidad de flujo ($j_s$) en relación con el radio de un grano genérico ($r_0$), la porosidad propia genérica ($q_0$), la porosidad ($f$), la densidad del líquido ($\rho_w$), la aceleración gravitacional ($g$), la viscosidad ($\eta$), la diferencia de altura ($\Delta h$) y el largo de la muestra ($\Delta L$) está representado por
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
y la conductividad hidráulica ($K_s$) está representado por
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
en el límite infinitesimal en el que la diferencia de altura ($\Delta h$) es igual a la diferencial de la altura de la columna ($dh$)
$\Delta h \rightarrow dh$
y en el que el largo de la muestra ($\Delta L$) es igual a la diferencial de distancia ($dx$)
$\Delta L \rightarrow dx$
esto nos lleva a
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
ID:(15226, 0)
Ecuación del flujo hacia un cuerpo de agua
Ecuación
La ecuación diferencial para calcular la altura de la columna de agua en el suelo ($h$) en función de la posición de la columna de agua en el suelo ($x$), el velocidad de precipitaciones ($r$) y la conductividad hidráulica ($K_s$) es:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
La ecuación para el producto de la altura de la columna de agua en el suelo ($h$) y la densidad de flujo ($j_s$) en función de la posición de la columna de agua en el suelo ($x$) y el velocidad de precipitaciones ($r$) es la siguiente:
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
y con la ecuación que describe la densidad de flujo ($j_s$) en términos de la conductividad hidráulica ($K_s$) y la posición de la columna de agua en el suelo ($x$):
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
podemos derivar la ecuación resultante de la siguiente manera:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
ID:(15824, 0)
Factor de precipitaciones
Ecuación
El factor de precipitaciones ($\mu_r$) se define utilizando el velocidad de precipitaciones ($r$), el distancia horizontal hasta la cúspide ($d$), la altura de referencia de la columna de agua ($h_0$) y la conductividad hidráulica ($K_s$) de la siguiente manera:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
ID:(15829, 0)
Altura del flujo hacia un cuerpo de agua
Ecuación
La ecuación para la altura de la columna de agua en el suelo ($h$) en función de la altura de referencia de la columna de agua ($h_0$), la posición de la columna de agua en el suelo ($x$), el distancia horizontal hasta la cúspide ($d$) y el factor de precipitaciones ($\mu_r$) es la siguiente:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
La ecuación para la altura de la columna de agua en el suelo ($h$) en función de la posición de la columna de agua en el suelo ($x$) y que depende de el velocidad de precipitaciones ($r$) y la conductividad hidráulica ($K_s$) es la siguiente:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
Podemos despejarla para facilitar la integración de la siguiente manera:
$\displaystyle\frac{d}{dx}\left(h\displaystyle\frac{dh}{dx}\right)=\displaystyle\frac{d}{dx}\displaystyle\frac{1}{2}\displaystyle\frac{d h^2}{dx} = \displaystyle\frac{1}{2}\displaystyle\frac{d^2 h^2}{dx^2}=- \displaystyle\frac{r}{K_s}$
Integrando con las condiciones que la profundidad en el borde con el cuerpo de agua es la altura de referencia de la columna de agua ($h_0$):
$h(0) = h_0$
y que el flujo en el distancia horizontal hasta la cúspide ($d$) es nulo:
$j_s(d) = -K_s\displaystyle\frac{d h}{dx}|_{x=d} = 0$
se obtiene con el factor de precipitaciones ($\mu_r$):
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
que:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
ID:(15825, 0)
Solución estatica en una dimensión
Ecuación
Podemos estudiar el caso estacionario, lo que implica que el producto de la altura de referencia de la columna de agua ($h_0$) por el flujo en un punto de referencia ($j_{s0}$) debe ser constante y, en particular, debe coincidir con el flujo de la lluvia representado por el velocidad de precipitaciones ($r$) y el distancia horizontal hasta la cúspide ($d$):
| $ h_0 j_{s0} = r d $ |
Si para la altura de la columna de agua en el suelo ($h$) dividido por la densidad de flujo ($j_s$), la ecuación con la posición de la columna de agua en el suelo ($x$) y el tiempo ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
en el caso estacionario se reduce a
$\displaystyle\frac{d}{dx} (h j_s) = 0$
esto implica que el producto de la altura de referencia de la columna de agua ($h_0$) y el flujo en un punto de referencia ($j_{s0}$) debe ser constante y, en particular, debe coincidir con el flujo de la lluvia representado por el velocidad de precipitaciones ($r$) y el distancia horizontal hasta la cúspide ($d$). Entonces se tiene que:
| $ h_0 j_{s0} = r d $ |
Nota: La ecuación diferencial es una ecuación diferencial ordinaria, ya que depende únicamente de la posición de la columna de agua en el suelo ($x$) y no de el tiempo ($t$).
ID:(15830, 0)
Densidad de flujo hacia un cuerpo de agua
Ecuación
La solución para la densidad de flujo ($j_s$) y el flujo en un punto de referencia ($j_{s0}$) dados la posición de la columna de agua en el suelo ($x$), el distancia horizontal hasta la cúspide ($d$) y el factor de precipitaciones ($\mu_r$) es la siguiente:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Con la solución para la altura de la columna de agua en el suelo ($h$) en función de la altura de referencia de la columna de agua ($h_0$), la posición de la columna de agua en el suelo ($x$), el distancia horizontal hasta la cúspide ($d$) y el factor de precipitaciones ($\mu_r$):
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
podemos calcular la densidad de flujo ($j_s$) utilizando la conductividad hidráulica ($K_s$) mediante:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
y aplicando el flujo en un punto de referencia ($j_{s0}$) y el velocidad de precipitaciones ($r$) en:
| $ h_0 j_{s0} = r d $ |
de esta manera obtenemos:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
ID:(15826, 0)