User:
Water table near a body of water
Storyboard 
In the case of the water table at the edge of a body of water whose level is not affected by its flow (such as a coastal or lacustrine area), the height of the water table above that body of water at the edge must be zero. Assuming the soil is homogeneous, the profile of the water table height above the water level can be calculated, meeting this boundary condition.
ID:(2083, 0)
Rain flow into a body of water
Concept
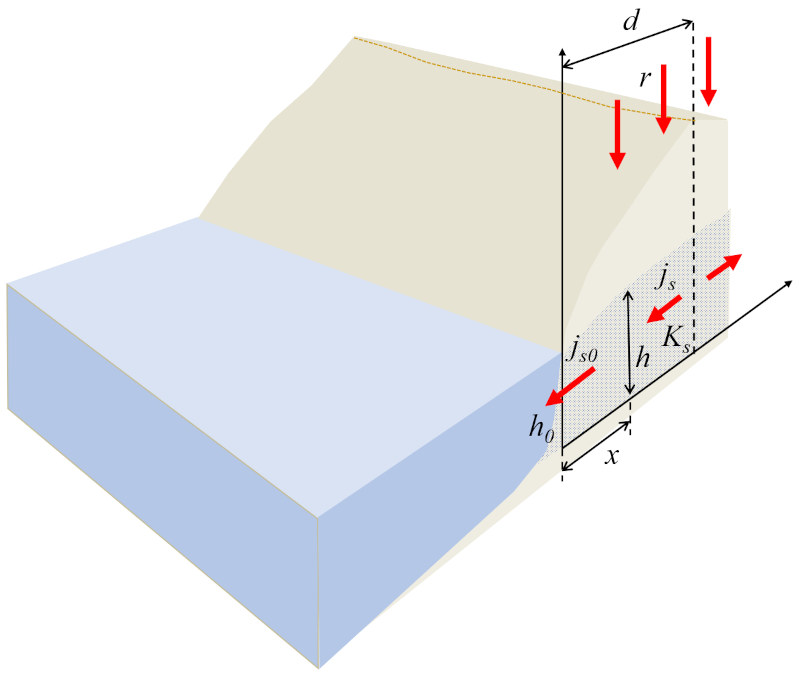
In the case of flow toward a body of water, the system can be modeled in a one-dimensional manner, where the height of the water column on the ground ($h$) is a function of the position of the water column on the ground ($x$). At the edge of the body of water, the longitudinal flow must equal the flow at a reference point ($j_{s0}$) multiplied by the reference height of the water column ($h_0$), which should correspond to the flow generated by the rainfall, i.e., the precipitation rate ($r$) multiplied by the horizontal distance to the top ($d$), represented as:
| $ h_0 j_{s0} = r d $ |
and depicted in the graph:
None
For modeling purposes, it is assumed that the soil is homogeneous with a constant the hydraulic conductivity ($K_s$) and that the flow moves from the area of maximum terrain height, which is at the horizontal distance to the top ($d$), towards the body of water.
ID:(15831, 0)
Solution height of flow into a body of water
Concept
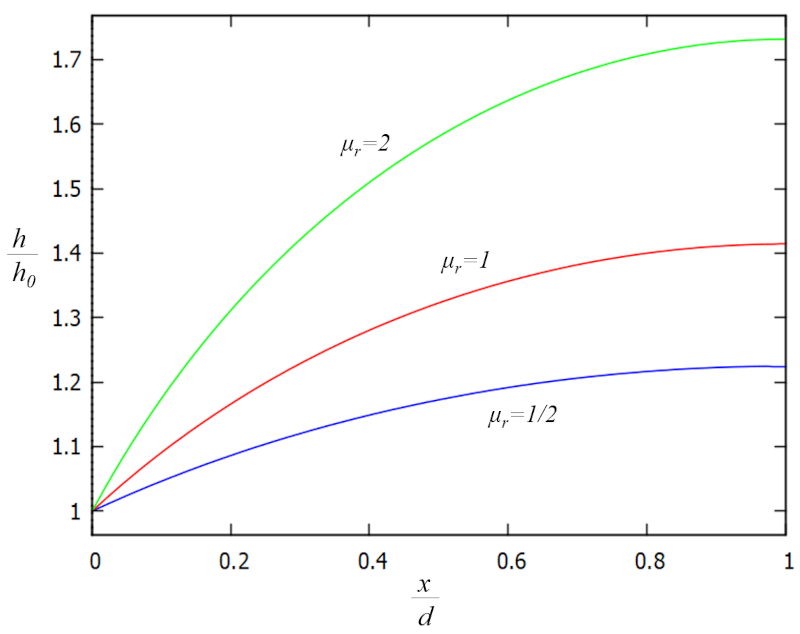
The solution to the one-dimensional flow equation towards a body of water, which calculates the value of the height of the water column on the ground ($h$) as a function of the reference height of the water column ($h_0$) and the position of the water column on the ground ($x$) at the edge of the body of water, along with the horizontal distance to the top ($d$) and the precipitation factor ($\mu_r$), is given by:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
This solution is graphically represented as a function of the additional factors $h/h_0$ and $x/d$ as follows:
None
The function depends on the factor the precipitation factor ($\mu_r$), which is particularly influenced by the precipitation rate ($r$) and the horizontal distance to the top ($d$), such that:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
This implies that if the effect of rainfall with $r d^2$ dominates over the soil's water flow capacity represented by $K_s h_0^2$, water will accumulate in the soil. Conversely, if the expression $K_s h_0^2$ dominates, the soil will tend to "drain" towards the body of water without significant retention.
ID:(15827, 0)
Flux density solution towards a body of water
Concept
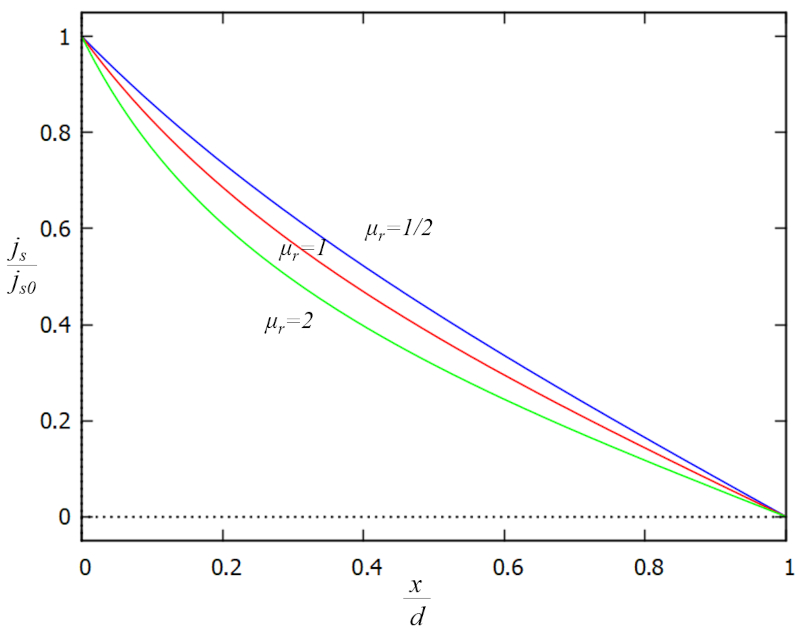
The solution obtained for the height and the parameters the flow at a reference point ($j_{s0}$) and the reference height of the water column ($h_0$) reveals that the flux density ($j_s$) is given by:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
We can graphically represent the flux density ($j_s$) as a function of the additional factors $j_s/j_{s0}$ and $x/s_0$ as follows:
None
It is noticeable that the flux density ($j_s$) continues to increase as we approach the channel, as the height of the water column on the ground ($h$) decreases. This increase is necessary to maintain the flow velocity in the flux density ($j_s$) or, alternatively, to increase it.
ID:(15828, 0)
Model
Top
Parameters
Variables
Calculations
to 
, then, select the variable: 
to 
Calculations
Calculations
Variable 
Given Calculate 
Target : Equation To be used 
Equations
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $
h / h_0 = sqrt(1 + mu_r * x *(2 - x / d )/ d )
$ h_0 j_{s0} = r d $
h_0 * j_s0 = r * d
$\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$
j_s / j_s0 = (1- x / d )/sqrt(1 + mu_r * x *(2- x / d )/ d )
$ j_s = - K_s \displaystyle\frac{ dh }{ dx }$
j_s = - K_s * dh / dx
$ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$
mu_r = r * d ^2/( K_s * h_0 ^2)
$\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $
@DIFF( h * @DIFF( h , x, 1), x ,1) = - r / K_s
$\displaystyle\frac{d}{dx}( h j_s )= r $
@DIFF( h * j_s , x ,1) = r
ID:(15822, 0)
Flow balance with rain
Equation
In the steady-state case, the variation in the position of the water column on the ground ($x$) of the product of the height of the water column on the ground ($h$) and the fluid Speed ($j_s$) must be equal to negative the precipitation rate ($r$):
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
If for the height of the water column on the ground ($h$) multiplied by the flux density ($j_s$), the equation for the position of the water column on the ground ($x$) and the time ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
in the steady-state case reduces to
$\displaystyle\frac{d}{dx} (h j_s) = 0$
this implies that the product of the height of the water column on the ground ($h$) and the flux density ($j_s$) is constant. In the case of rain, water adheres to the entire surface at a rate of a precipitation rate ($r$):
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Note: The differential equation is an ordinary differential equation, as it depends solely on the position of the water column on the ground ($x$) and not on the time ($t$).
ID:(15823, 0)
Flow density and hydraulic conductivity
Equation
The flux density ($j_s$) can be expressed in terms of the hydraulic conductivity ($K_s$), the height of the water column on the ground ($h$), and the position of the water column on the ground ($x$) as follows:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Given that the flux density ($j_s$) in relation to the radius of a generic grain ($r_0$), the generic own porosity ($q_0$), the porosity ($f$), the liquid density ($\rho_w$), the gravitational Acceleration ($g$), the viscosity ($\eta$), the height difference ($\Delta h$), and the sample length ($\Delta L$) is represented by
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
and the hydraulic conductivity ($K_s$) is represented by
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
in the infinitesimal limit where the height difference ($\Delta h$) equals the column height differential ($dh$)
$\Delta h \rightarrow dh$
and where the sample length ($\Delta L$) equals the distance differential ($dx$)
$\Delta L \rightarrow dx$
this leads us to
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
ID:(15226, 0)
Equation of flow into a body of water
Equation
The differential equation to calculate the height of the water column on the ground ($h$) as a function of the position of the water column on the ground ($x$), the precipitation rate ($r$), and the hydraulic conductivity ($K_s$) is:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
The equation for the product of the height of the water column on the ground ($h$) and the flux density ($j_s$) as a function of the position of the water column on the ground ($x$) and the precipitation rate ($r$) is as follows:
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
With the equation that describes the flux density ($j_s$) in terms of the hydraulic conductivity ($K_s$) and the position of the water column on the ground ($x$):
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
we can derive the resulting equation as follows:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
ID:(15824, 0)
Precipitation factor
Equation
The precipitation factor ($\mu_r$) is defined using the precipitation rate ($r$), the horizontal distance to the top ($d$), the reference height of the water column ($h_0$), and the hydraulic conductivity ($K_s$) as follows:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
ID:(15829, 0)
Height of flow into a body of water
Equation
The equation for the height of the water column on the ground ($h$) as a function of the reference height of the water column ($h_0$), the position of the water column on the ground ($x$), the horizontal distance to the top ($d$), and the precipitation factor ($\mu_r$) is as follows:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
The equation for the height of the water column on the ground ($h$) as a function of the position of the water column on the ground ($x$), which depends on the precipitation rate ($r$) and the hydraulic conductivity ($K_s$), is as follows:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
We can rearrange it for easier integration as follows:
$\displaystyle\frac{d}{dx}\left(h\displaystyle\frac{dh}{dx}\right)=\displaystyle\frac{d}{dx}\displaystyle\frac{1}{2}\displaystyle\frac{d h^2}{dx} = \displaystyle\frac{1}{2}\displaystyle\frac{d^2 h^2}{dx^2}=- \displaystyle\frac{r}{K_s}$
Integrating with the conditions that the depth at the edge of the body of water is the reference height of the water column ($h_0$):
$h(0) = h_0$
and that the flow at the horizontal distance to the top ($d$) is zero:
$j_s(d) = -K_s\displaystyle\frac{d h}{dx}|_{x=d} = 0$
we get with the precipitation factor ($\mu_r$):
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
that:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
ID:(15825, 0)
Static solution in one dimension
Equation
We can study the steady-state case, which implies that the product of the reference height of the water column ($h_0$) and the flow at a reference point ($j_{s0}$) must be constant and, in particular, must match the rainfall flow given by the precipitation rate ($r$) and the horizontal distance to the top ($d$):
| $ h_0 j_{s0} = r d $ |
If for the height of the water column on the ground ($h$) divided by the flux density ($j_s$), the equation with the position of the water column on the ground ($x$) and the time ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
in the steady-state case reduces to
$\displaystyle\frac{d}{dx} (h j_s) = 0$
this implies that the product of the reference height of the water column ($h_0$) and the flow at a reference point ($j_{s0}$) must be constant and, in particular, must match the rainfall flow given by the precipitation rate ($r$) and the horizontal distance to the top ($d$). Therefore, we have:
| $ h_0 j_{s0} = r d $ |
Note: The differential equation is an ordinary differential equation, as it depends solely on the position of the water column on the ground ($x$) and not on the time ($t$).
ID:(15830, 0)
Flow density into a body of water
Equation
The solution for the flux density ($j_s$) and the flow at a reference point ($j_{s0}$) given the position of the water column on the ground ($x$), the horizontal distance to the top ($d$), and the precipitation factor ($\mu_r$) is as follows:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
With the solution for the height of the water column on the ground ($h$) based on the reference height of the water column ($h_0$), the position of the water column on the ground ($x$), the horizontal distance to the top ($d$), and the precipitation factor ($\mu_r$):
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
we can calculate the flux density ($j_s$) using the hydraulic conductivity ($K_s$) with:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
and applying the flow at a reference point ($j_{s0}$) and the precipitation rate ($r$) in:
| $ h_0 j_{s0} = r d $ |
in this way, we obtain:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
ID:(15826, 0)