Utilisateur:
Nappe phréatique à proximité d'un plan d'eau
Storyboard 
Dans le cas de la nappe phréatique en bordure d'un plan d'eau dont le niveau n'est pas affecté par son flux (comme une zone côtière ou lacustre), la hauteur de la nappe phréatique au-dessus de ce plan d'eau doit être nulle à la bordure. En supposant que le sol soit homogène, on peut calculer le profil de la hauteur de la nappe phréatique par rapport au niveau de l'eau, en respectant cette condition de bord.
ID:(2083, 0)
La pluie s'écoule dans un plan d'eau
Concept
Dans le cas du flux vers un corps d'eau, le système peut être modélisé de manière unidimensionnelle, où A hauteur de la colonne d'eau au sol ($h$) est une fonction de a position de la colonne d'eau au sol ($x$). Au bord du corps d'eau, le flux longitudinal doit être égal à Le flux à un point de référence ($j_{s0}$) multiplié par a hauteur de référence de la colonne d'eau ($h_0$), ce qui doit correspondre au flux généré par la pluie, c'est-à-dire le taux de précipitation ($r$) multiplié par le distance horizontale jusqu'au sommet ($d$), représenté comme suit :
| $ h_0 j_{s0} = r d $ |
et illustré dans le graphique :
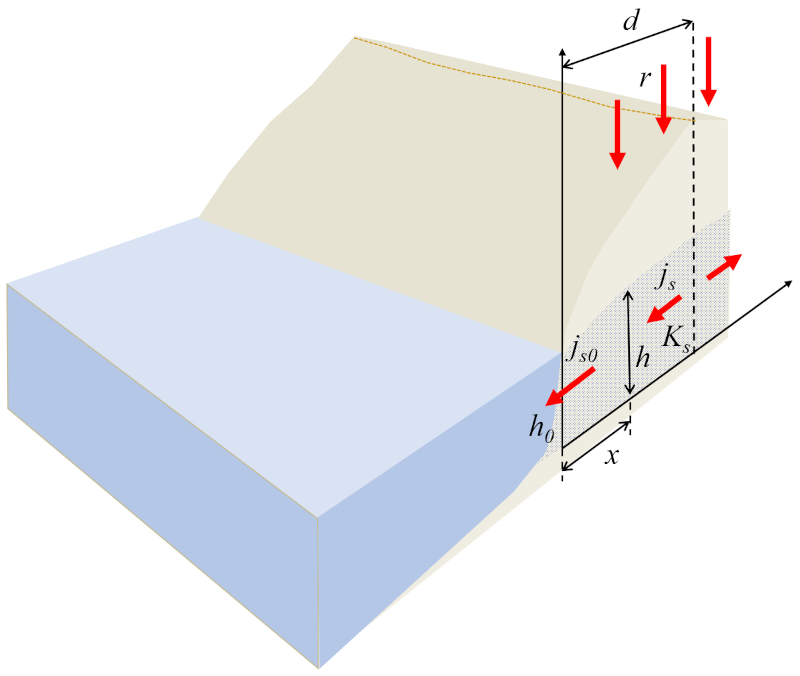
Pour la modélisation, il est supposé que le sol est homogène avec une constante de a conductivité hydraulique ($K_s$) et que le flux se déplace de la zone de hauteur maximale du terrain, située à Le distance horizontale jusqu'au sommet ($d$), vers le corps d'eau.
ID:(15831, 0)
Hauteur d'écoulement de la solution dans un plan d'eau
Concept
La solution de l'équation de flux unidimensionnelle vers un corps d'eau, qui calcule la valeur de a hauteur de la colonne d'eau au sol ($h$) en fonction de a hauteur de référence de la colonne d'eau ($h_0$) et a position de la colonne d'eau au sol ($x$) au bord du corps d'eau, ainsi que de le distance horizontale jusqu'au sommet ($d$) et le facteur de précipitation ($\mu_r$), est la suivante :
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
Cette solution est représentée graphiquement en fonction des facteurs supplémentaires $h/h_0$ et $x/d$ comme suit :
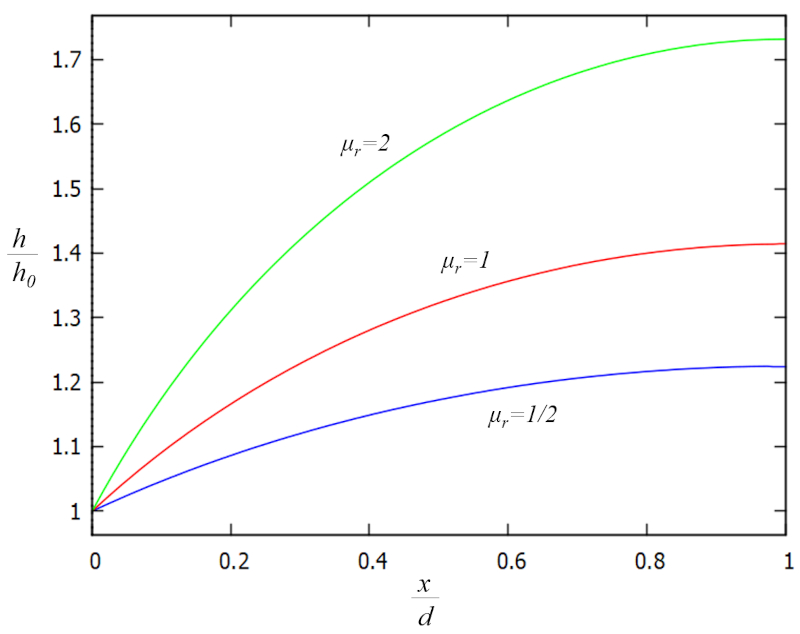
La fonction dépend du facteur le facteur de précipitation ($\mu_r$), qui est particulièrement influencé par le taux de précipitation ($r$) et le distance horizontale jusqu'au sommet ($d$), de sorte que :
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
Cela signifie que si l'effet de la pluie avec $r d^2$ prédomine sur la capacité de flux de l'eau à travers le sol, représentée par $K_s h_0^2$, l'eau s'accumulera dans le sol. En revanche, si l'expression $K_s h_0^2$ prédomine, le sol aura tendance à "se vider" vers le corps d'eau sans une rétention significative.
ID:(15827, 0)
Solution de densité de flux vers un plan d'eau
Concept
La solution obtenue pour la hauteur et les paramètres le flux à un point de référence ($j_{s0}$) et a hauteur de référence de la colonne d'eau ($h_0$) révèle que a densité de flux ($j_s$) est donné par :
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Nous pouvons représenter graphiquement a densité de flux ($j_s$) en fonction des facteurs additionnels $j_s/j_{s0}$ et $x/s_0$ de la manière suivante :
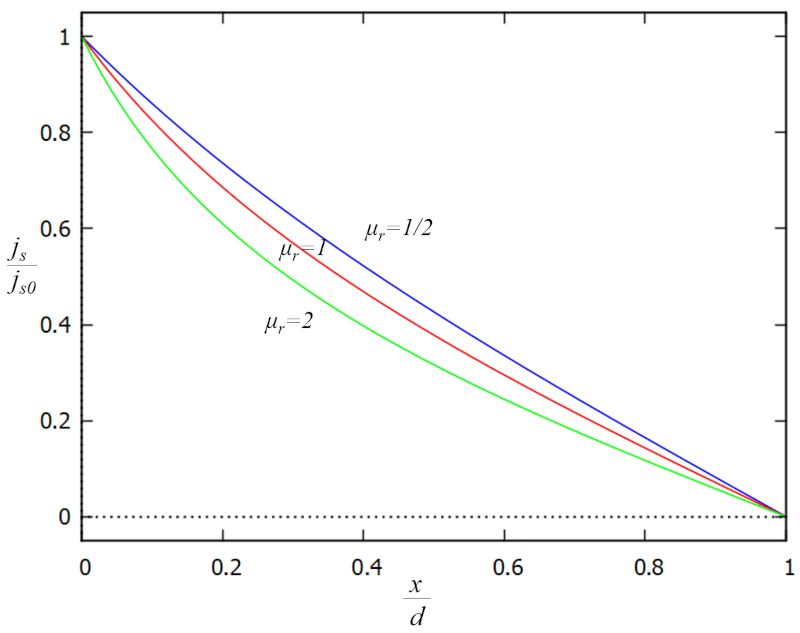
Il est notable que a densité de flux ($j_s$) continue d'augmenter à mesure que nous nous approchons du canal, car a hauteur de la colonne d'eau au sol ($h$) diminue. Cette augmentation est nécessaire pour maintenir la vitesse de l'écoulement dans a densité de flux ($j_s$) ou, en alternance, pour l'augmenter.
ID:(15828, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $
h / h_0 = sqrt(1 + mu_r * x *(2 - x / d )/ d )
$ h_0 j_{s0} = r d $
h_0 * j_s0 = r * d
$\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$
j_s / j_s0 = (1- x / d )/sqrt(1 + mu_r * x *(2- x / d )/ d )
$ j_s = - K_s \displaystyle\frac{ dh }{ dx }$
j_s = - K_s * dh / dx
$ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$
mu_r = r * d ^2/( K_s * h_0 ^2)
$\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $
@DIFF( h * @DIFF( h , x, 1), x ,1) = - r / K_s
$\displaystyle\frac{d}{dx}( h j_s )= r $
@DIFF( h * j_s , x ,1) = r
ID:(15822, 0)
Bilan des flux avec la pluie
Équation
Dans le cas stationnaire, la variation de a position de la colonne d'eau au sol ($x$) du produit de a hauteur de la colonne d'eau au sol ($h$) et a vitesse du fluide ($j_s$) doit être égale à moins le taux de précipitation ($r$) :
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Si pour a hauteur de la colonne d'eau au sol ($h$) multiplié par a densité de flux ($j_s$), l'équation pour a position de la colonne d'eau au sol ($x$) et le temps ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
dans le cas stationnaire se réduit à
$\displaystyle\frac{d}{dx} (h j_s) = 0$
cela implique que le produit de a hauteur de la colonne d'eau au sol ($h$) par a densité de flux ($j_s$) est constant. En cas de pluie, l'eau s'adhère à toute la surface à un taux de un taux de précipitation ($r$) :
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Note : L'équation différentielle est une équation différentielle ordinaire, car elle dépend uniquement de a position de la colonne d'eau au sol ($x$) et non de le temps ($t$).
ID:(15823, 0)
Densité d'écoulement et conductivité hydraulique
Équation
A densité de flux ($j_s$) peut être exprimé en termes de a conductivité hydraulique ($K_s$), a hauteur de la colonne d'eau au sol ($h$) et a position de la colonne d'eau au sol ($x$) de la manière suivante :
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Étant donné que a densité de flux ($j_s$) par rapport à Le rayon d'un grain générique ($r_0$), a porosité propre générique ($q_0$), a porosité ($f$), a densité du liquide ($\rho_w$), a accélération gravitationnelle ($g$), a viscosité ($\eta$), a différence de hauteur ($\Delta h$) et le longueur de l'échantillon ($\Delta L$) est représenté par
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
et a conductivité hydraulique ($K_s$) est représenté par
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
dans la limite infinitésimale où A différence de hauteur ($\Delta h$) est égal à A différentiel de hauteur de colonne ($dh$)
$\Delta h \rightarrow dh$
et où Le longueur de l'échantillon ($\Delta L$) est égal à A différentiel de distance ($dx$)
$\Delta L \rightarrow dx$
cela nous conduit à
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
ID:(15226, 0)
Équation de débit dans une masse deau
Équation
L'équation différentielle pour calculer a hauteur de la colonne d'eau au sol ($h$) en fonction de a position de la colonne d'eau au sol ($x$), le taux de précipitation ($r$) et a conductivité hydraulique ($K_s$) est la suivante :
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
L'équation pour le produit de a hauteur de la colonne d'eau au sol ($h$) et a densité de flux ($j_s$) en fonction de a position de la colonne d'eau au sol ($x$) et le taux de précipitation ($r$) est la suivante :
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Avec l'équation qui décrit a densité de flux ($j_s$) en termes de a conductivité hydraulique ($K_s$) et a position de la colonne d'eau au sol ($x$) :
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
nous pouvons dériver l'équation résultante de la manière suivante :
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
ID:(15824, 0)
Facteur de précipitation
Équation
Le facteur de précipitation ($\mu_r$) est défini en utilisant le taux de précipitation ($r$), le distance horizontale jusqu'au sommet ($d$), a hauteur de référence de la colonne d'eau ($h_0$) et a conductivité hydraulique ($K_s$) comme suit :
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
ID:(15829, 0)
Hauteur d'écoulement dans un plan d'eau
Équation
L'équation pour a hauteur de la colonne d'eau au sol ($h$) en fonction de a hauteur de référence de la colonne d'eau ($h_0$), a position de la colonne d'eau au sol ($x$), le distance horizontale jusqu'au sommet ($d$) et le facteur de précipitation ($\mu_r$) est la suivante :
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
L'équation pour a hauteur de la colonne d'eau au sol ($h$) en fonction de a position de la colonne d'eau au sol ($x$) et qui dépend de le taux de précipitation ($r$) et a conductivité hydraulique ($K_s$) est la suivante :
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
Nous pouvons la réarranger pour faciliter l'intégration de la manière suivante :
$\displaystyle\frac{d}{dx}\left(h\displaystyle\frac{dh}{dx}\right)=\displaystyle\frac{d}{dx}\displaystyle\frac{1}{2}\displaystyle\frac{d h^2}{dx} = \displaystyle\frac{1}{2}\displaystyle\frac{d^2 h^2}{dx^2}=- \displaystyle\frac{r}{K_s}$
En intégrant avec les conditions que la profondeur au bord du plan d'eau est a hauteur de référence de la colonne d'eau ($h_0$) :
$h(0) = h_0$
et que le flux à Le distance horizontale jusqu'au sommet ($d$) est nul :
$j_s(d) = -K_s\displaystyle\frac{d h}{dx}|_{x=d} = 0$
nous obtenons avec le facteur de précipitation ($\mu_r$) :
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
que :
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
"
ID:(15825, 0)
Solution statique en une dimension
Équation
Nous pouvons étudier le cas stationnaire, ce qui implique que le produit de a hauteur de référence de la colonne d'eau ($h_0$) par le flux à un point de référence ($j_{s0}$) doit être constant et, en particulier, doit correspondre au flux de pluie donné par le taux de précipitation ($r$) et le distance horizontale jusqu'au sommet ($d$) :
| $ h_0 j_{s0} = r d $ |
Si pour a hauteur de la colonne d'eau au sol ($h$) divisé par a densité de flux ($j_s$), l'équation avec a position de la colonne d'eau au sol ($x$) et le temps ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
dans le cas stationnaire se réduit à
$\displaystyle\frac{d}{dx} (h j_s) = 0$
cela implique que le produit de a hauteur de référence de la colonne d'eau ($h_0$) et le flux à un point de référence ($j_{s0}$) doit être constant et, en particulier, doit correspondre au flux de pluie donné par le taux de précipitation ($r$) et le distance horizontale jusqu'au sommet ($d$). Par conséquent, nous avons :
| $ h_0 j_{s0} = r d $ |
Remarque : L'équation différentielle est une équation différentielle ordinaire, car elle dépend uniquement de a position de la colonne d'eau au sol ($x$) et non de le temps ($t$).
ID:(15830, 0)
Densité du débit dans une masse d'eau
Équation
La solution pour a densité de flux ($j_s$) et le flux à un point de référence ($j_{s0}$) donnée a position de la colonne d'eau au sol ($x$), le distance horizontale jusqu'au sommet ($d$), et le facteur de précipitation ($\mu_r$) est la suivante :
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Avec la solution pour a hauteur de la colonne d'eau au sol ($h$) en fonction de a hauteur de référence de la colonne d'eau ($h_0$), a position de la colonne d'eau au sol ($x$), le distance horizontale jusqu'au sommet ($d$) et le facteur de précipitation ($\mu_r$) :
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
nous pouvons calculer a densité de flux ($j_s$) en utilisant a conductivité hydraulique ($K_s$) avec :
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
et en appliquant le flux à un point de référence ($j_{s0}$) et le taux de précipitation ($r$) dans :
| $ h_0 j_{s0} = r d $ |
ainsi, nous obtenons :
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
ID:(15826, 0)