Benützer:
Grundwasserspiegel in der Nähe eines Gewässers
Storyboard 
Im Falle eines Grundwasserspiegels am Rand eines Gewässers, dessen Pegel nicht durch seinen Fluss beeinflusst wird (wie in einem Küsten- oder Seengebiet), muss die Höhe des Grundwasserspiegels über dem Gewässerrand null sein. Unter der Annahme, dass der Boden homogen ist, kann das Profil der Höhe des Grundwasserspiegels über dem Wasserspiegel berechnet werden, wobei diese Randbedingung erfüllt wird.
ID:(2083, 0)
Regen fließt in ein Gewässer
Konzept
Im Fall des Flusses zu einem Gewässer kann das System eindimensional modelliert werden, wobei die Höhe der Wassersäule am Boden ($h$) eine Funktion von die Position der Wassersäule am Boden ($x$) ist. Am Rand des Gewässers muss der longitudinale Fluss gleich der Strömung an einem Referenzpunkt ($j_{s0}$) mal die Referenzhöhe der Wassersäule ($h_0$) sein, was dem durch den Regen erzeugten Fluss entsprechen sollte, d.h. Der Niederschlagsmenge ($r$) mal der Horizontaler Abstand bis zur Spitze ($d$), dargestellt als:
| $ h_0 j_{s0} = r d $ |
und in der Grafik dargestellt:
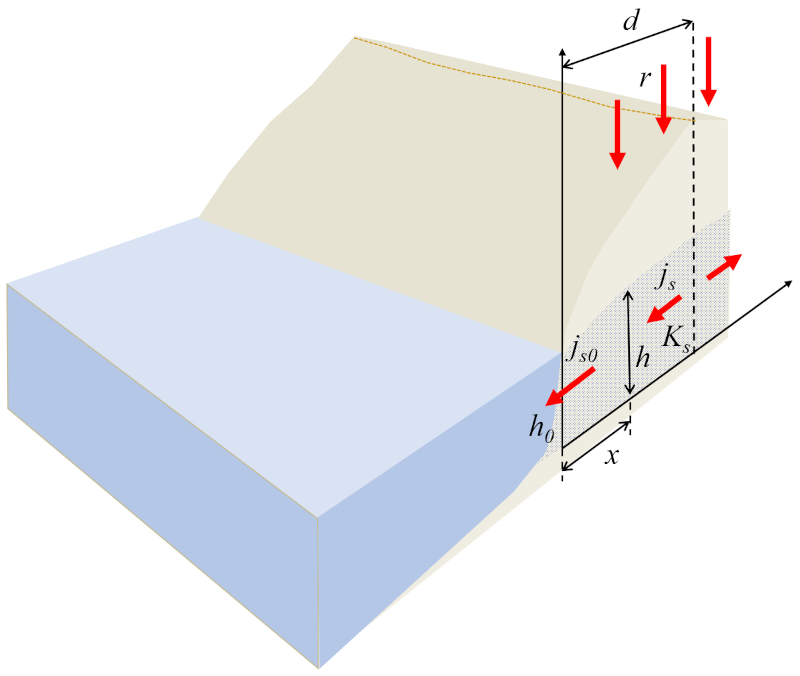
None
Für das Modell wird angenommen, dass der Boden homogen mit einer konstanten die Hydraulische Leitfähigkeit ($K_s$) ist und dass der Fluss von der Zone mit der maximalen Geländehöhe, die sich bei der Horizontaler Abstand bis zur Spitze ($d$) befindet, zum Gewässer fließt.
ID:(15831, 0)
Fließhöhe der Lösung in ein Gewässer
Konzept
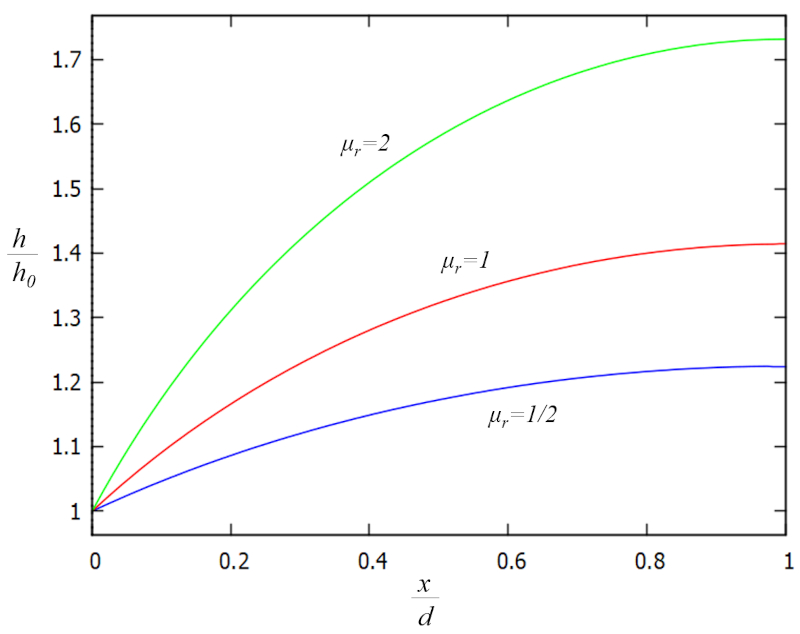
Die Lösung der eindimensionalen Flussgleichung zu einem Gewässer, die den Wert von die Höhe der Wassersäule am Boden ($h$) als Funktion von die Referenzhöhe der Wassersäule ($h_0$) und die Position der Wassersäule am Boden ($x$) am Rand des Gewässers zusammen mit der Horizontaler Abstand bis zur Spitze ($d$) und der Niederschlagsfaktor ($\mu_r$) berechnet, lautet:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
Diese Lösung wird grafisch in Abhängigkeit von den zusätzlichen Faktoren $h/h_0$ und $x/d$ wie folgt dargestellt:
None
Die Funktion hängt vom Faktor der Niederschlagsfaktor ($\mu_r$) ab, der insbesondere von der Niederschlagsmenge ($r$) und der Horizontaler Abstand bis zur Spitze ($d$) beeinflusst wird, sodass:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
Das bedeutet, dass, wenn der Einfluss des Niederschlags mit $r d^2$ die Wasserflusskapazität des Bodens, dargestellt durch $K_s h_0^2$, überwiegt, Wasser im Boden angereichert wird. Im Gegensatz dazu wird, wenn die Expression $K_s h_0^2$ dominiert, der Boden dazu neigen, zum Gewässer entleert zu werden, ohne wesentliche Rückhaltung.
ID:(15827, 0)
Flussdichtelösung in Richtung eines Gewässers
Konzept
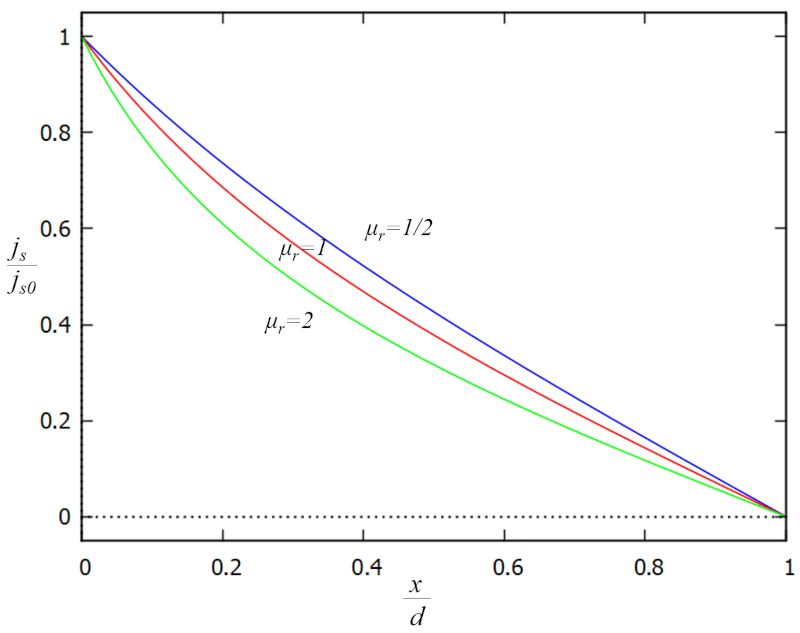
Die erhaltene Lösung für die Höhe und die Parameter der Strömung an einem Referenzpunkt ($j_{s0}$) und die Referenzhöhe der Wassersäule ($h_0$) zeigt, dass die Flussdichte ($j_s$) wie folgt berechnet wird:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Wir können die Flussdichte ($j_s$) graphisch in Abhängigkeit von den zusätzlichen Faktoren $j_s/j_{s0}$ und $x/s_0$ wie folgt darstellen:
None
Es fällt auf, dass die Flussdichte ($j_s$) weiter zunimmt, je näher wir dem Kanal kommen, da die Höhe der Wassersäule am Boden ($h$) abnimmt. Dieser Anstieg ist erforderlich, um die Fließgeschwindigkeit in die Flussdichte ($j_s$) aufrechtzuerhalten oder alternativ, um sie zu erhöhen.
ID:(15828, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $
h / h_0 = sqrt(1 + mu_r * x *(2 - x / d )/ d )
$ h_0 j_{s0} = r d $
h_0 * j_s0 = r * d
$\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$
j_s / j_s0 = (1- x / d )/sqrt(1 + mu_r * x *(2- x / d )/ d )
$ j_s = - K_s \displaystyle\frac{ dh }{ dx }$
j_s = - K_s * dh / dx
$ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$
mu_r = r * d ^2/( K_s * h_0 ^2)
$\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $
@DIFF( h * @DIFF( h , x, 1), x ,1) = - r / K_s
$\displaystyle\frac{d}{dx}( h j_s )= r $
@DIFF( h * j_s , x ,1) = r
ID:(15822, 0)
Strömungsausgleich mit Regen
Gleichung
Im stationären Fall muss die Variation von die Position der Wassersäule am Boden ($x$) des Produkts von die Höhe der Wassersäule am Boden ($h$) und die Flüssigkeitsgeschwindigkeit ($j_s$) gleich minus der Niederschlagsmenge ($r$) sein:
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Wenn für die Höhe der Wassersäule am Boden ($h$) multipliziert mit die Flussdichte ($j_s$) die Gleichung für die Position der Wassersäule am Boden ($x$) und der Zeit ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
im stationären Fall zu
$\displaystyle\frac{d}{dx} (h j_s) = 0$
wird, impliziert dies, dass das Produkt von die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) konstant ist. Im Falle von Regen haftet das Wasser mit einer Rate von ein Niederschlagsmenge ($r$) auf der gesamten Oberfläche:
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Hinweis: Die Differentialgleichung ist eine gewöhnliche Differentialgleichung, da sie ausschließlich von die Position der Wassersäule am Boden ($x$) und nicht von der Zeit ($t$) abhängt.
ID:(15823, 0)
Strömungsdichte und hydraulische Leitfähigkeit
Gleichung
Die Flussdichte ($j_s$) kann in Bezug auf die Hydraulische Leitfähigkeit ($K_s$), die Höhe der Wassersäule am Boden ($h$) und die Position der Wassersäule am Boden ($x$) wie folgt ausgedrückt werden:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
Angesichts der Tatsache, dass die Flussdichte ($j_s$) in Bezug auf der Radius einer generischen Korns ($r_0$), die Generische eigene Porosität ($q_0$), die Porosität ($f$), die Flüssigkeitsdichte ($\rho_w$), die Gravitationsbeschleunigung ($g$), die Viskosität ($\eta$), die Höhendifferenz ($\Delta h$) und der Probenlänge ($\Delta L$) dargestellt wird durch
| $ j_s =-\displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }\displaystyle\frac{ \Delta h }{ \Delta L }$ |
und die Hydraulische Leitfähigkeit ($K_s$) wird dargestellt durch
| $ K_s \equiv \displaystyle\frac{ r_0 ^2 }{8 q_0 }\displaystyle\frac{ f ^3 }{(1- f )^2}\displaystyle\frac{ \rho_w g }{ \eta }$ |
im infinitesimalen Grenzwert, in dem die Höhendifferenz ($\Delta h$) gleich die Säulenhöhenunterschied ($dh$) ist
$\Delta h \rightarrow dh$
und in dem der Probenlänge ($\Delta L$) gleich die Distanzdifferenz ($dx$) ist
$\Delta L \rightarrow dx$
führt uns dies zu
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
ID:(15226, 0)
Gleichung für den Zufluss in ein Gewässer
Gleichung
Die Differentialgleichung zur Berechnung von die Höhe der Wassersäule am Boden ($h$) in Abhängigkeit von die Position der Wassersäule am Boden ($x$), der Niederschlagsmenge ($r$) und die Hydraulische Leitfähigkeit ($K_s$) lautet:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
Die Gleichung für das Produkt von die Höhe der Wassersäule am Boden ($h$) und die Flussdichte ($j_s$) in Abhängigkeit von die Position der Wassersäule am Boden ($x$) und der Niederschlagsmenge ($r$) lautet wie folgt:
| $\displaystyle\frac{d}{dx}( h j_s )= r $ |
Mit der Gleichung, die die Flussdichte ($j_s$) in Bezug auf die Hydraulische Leitfähigkeit ($K_s$) und die Position der Wassersäule am Boden ($x$) beschreibt:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
können wir die resultierende Gleichung wie folgt ableiten:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
ID:(15824, 0)
Niederschlagsfaktor
Gleichung
Der Niederschlagsfaktor ($\mu_r$) wird unter Verwendung von der Niederschlagsmenge ($r$), der Horizontaler Abstand bis zur Spitze ($d$), die Referenzhöhe der Wassersäule ($h_0$) und die Hydraulische Leitfähigkeit ($K_s$) wie folgt definiert:
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
ID:(15829, 0)
Fließhöhe in ein Gewässer
Gleichung
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) in Abhängigkeit von die Referenzhöhe der Wassersäule ($h_0$), die Position der Wassersäule am Boden ($x$), der Horizontaler Abstand bis zur Spitze ($d$) und der Niederschlagsfaktor ($\mu_r$) lautet wie folgt:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
Die Gleichung für die Höhe der Wassersäule am Boden ($h$) in Abhängigkeit von die Position der Wassersäule am Boden ($x$) und die von der Niederschlagsmenge ($r$) und die Hydraulische Leitfähigkeit ($K_s$) abhängt, lautet wie folgt:
| $\displaystyle\frac{ d }{ dx }\left( h \displaystyle\frac{ dh }{ dx }\right) = -\displaystyle\frac{ r }{ K_s } $ |
Wir können sie wie folgt umstellen, um die Integration zu erleichtern:
$\displaystyle\frac{d}{dx}\left(h\displaystyle\frac{dh}{dx}\right)=\displaystyle\frac{d}{dx}\displaystyle\frac{1}{2}\displaystyle\frac{d h^2}{dx} = \displaystyle\frac{1}{2}\displaystyle\frac{d^2 h^2}{dx^2}=- \displaystyle\frac{r}{K_s}$
Integration mit den Bedingungen, dass die Tiefe am Rand des Gewässers die Referenzhöhe der Wassersäule ($h_0$) beträgt:
$h(0) = h_0$
und dass der Fluss bei der Horizontaler Abstand bis zur Spitze ($d$) null ist:
$j_s(d) = -K_s\displaystyle\frac{d h}{dx}|_{x=d} = 0$
wir erhalten mit der Niederschlagsfaktor ($\mu_r$):
| $ \mu_r \equiv \displaystyle\frac{ r }{ K_s }\displaystyle\frac{ d ^2}{ h_0 ^2}$ |
dass:
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
ID:(15825, 0)
Statische Lösung in einer Dimension
Gleichung
Wir können den stationären Fall untersuchen, was impliziert, dass das Produkt von die Referenzhöhe der Wassersäule ($h_0$) und der Strömung an einem Referenzpunkt ($j_{s0}$) konstant sein muss und insbesondere mit dem durch der Niederschlagsmenge ($r$) und der Horizontaler Abstand bis zur Spitze ($d$) gegebenen Regenfluss übereinstimmen muss:
| $ h_0 j_{s0} = r d $ |
Wenn für die Höhe der Wassersäule am Boden ($h$) geteilt durch die Flussdichte ($j_s$) die Gleichung mit die Position der Wassersäule am Boden ($x$) und der Zeit ($t$)
| $\displaystyle\frac{\partial h}{\partial t} = - \displaystyle\frac{\partial}{\partial x}( h j_s )$ |
im stationären Fall zu
$\displaystyle\frac{d}{dx} (h j_s) = 0$
wird, bedeutet dies, dass das Produkt von die Referenzhöhe der Wassersäule ($h_0$) und der Strömung an einem Referenzpunkt ($j_{s0}$) konstant sein muss und insbesondere mit dem durch der Niederschlagsmenge ($r$) und der Horizontaler Abstand bis zur Spitze ($d$) gegebenen Regenfluss übereinstimmen muss. Daher gilt:
| $ h_0 j_{s0} = r d $ |
Hinweis: Die Differentialgleichung ist eine gewöhnliche Differentialgleichung, da sie ausschließlich von die Position der Wassersäule am Boden ($x$) und nicht von der Zeit ($t$) abhängt.
ID:(15830, 0)
Fließdichte in ein Gewässer
Gleichung
Die Lösung für die Flussdichte ($j_s$) und der Strömung an einem Referenzpunkt ($j_{s0}$) unter den gegebenen die Position der Wassersäule am Boden ($x$), der Horizontaler Abstand bis zur Spitze ($d$) und der Niederschlagsfaktor ($\mu_r$) lautet wie folgt:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
Mit der Lösung für die Höhe der Wassersäule am Boden ($h$) basierend auf die Referenzhöhe der Wassersäule ($h_0$), die Position der Wassersäule am Boden ($x$), der Horizontaler Abstand bis zur Spitze ($d$) und der Niederschlagsfaktor ($\mu_r$):
| $ \displaystyle\frac{ h }{ h_0 } = \sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)} $ |
können wir die Flussdichte ($j_s$) unter Verwendung von die Hydraulische Leitfähigkeit ($K_s$) berechnen mit:
| $ j_s = - K_s \displaystyle\frac{ dh }{ dx }$ |
und durch Anwendung von der Strömung an einem Referenzpunkt ($j_{s0}$) und der Niederschlagsmenge ($r$) in:
| $ h_0 j_{s0} = r d $ |
auf diese Weise erhalten wir:
| $\displaystyle\frac{ j_s }{ j_{s0} } = \displaystyle\frac{\left(1- \displaystyle\frac{ x }{ d }\right)}{\sqrt{1 + \mu_r \displaystyle\frac{ x }{ d }\left(2- \displaystyle\frac{ x }{ d }\right)}}$ |
ID:(15826, 0)