Usuario:
Movimiento de los océanos, drifters
Storyboard 
El movimiento en la superficie de los océanos surge de la interacción con la atmósfera y está condicionado por las corrientes más profundas (más de 15 metros). En primera aproximación, se puede considerar como un flujo a velocidad constante con vórtices estables o que son arrastrados por él.
ID:(1519, 0)
Mecanismos
Iframe
Mecanismos
ID:(15449, 0)
Movimientos del océano
Video
El movimiento del océano es generado en la superficie por el movimiento del aire mientras que en la profundidad por variaciones en la densidad condicionados por temperatura y salinidad. En el siguiente video de NASA se muestran distintos efectos:
ID:(11485, 0)
Corriente del golfo
Imagen
Una de las corrientes mas importantes del océano atlántico es la llamada corriente del golfo. Esta lleva aguas cálidas desde el caribe hasta Europa contribuyendo a un clima mas templado en esta área:
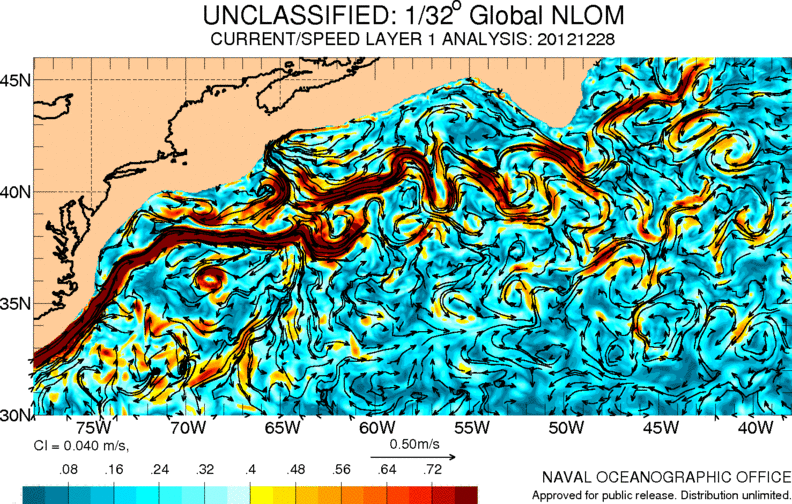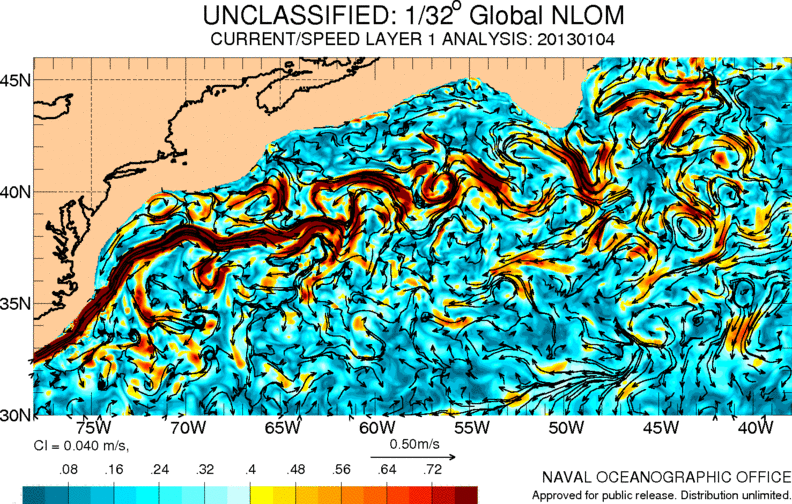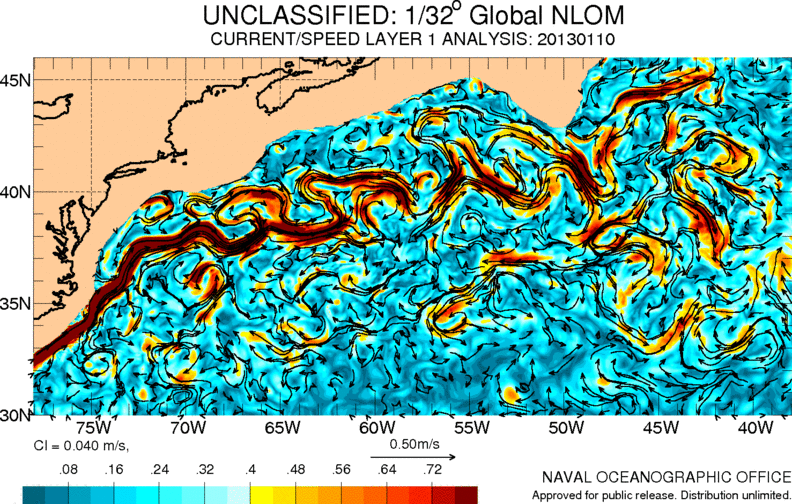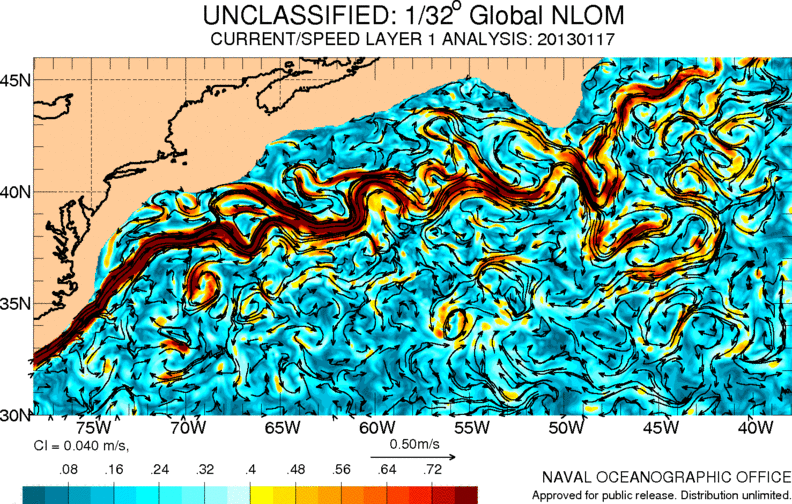
ID:(11486, 0)
Corrientes en centroamérica y el caribe
Imagen
La corriente del golfo se origina en el caribe en donde ademas existe una serie de circulación asociada a los movimientos de las masas de aire en la región:
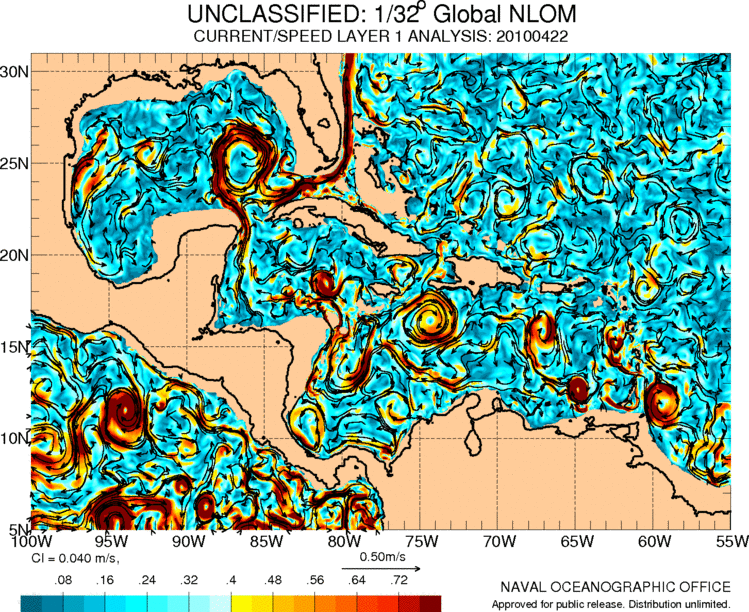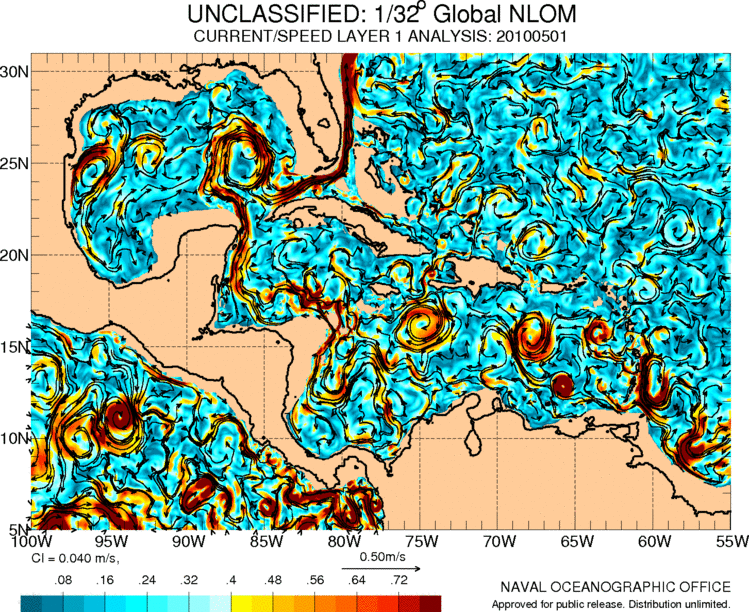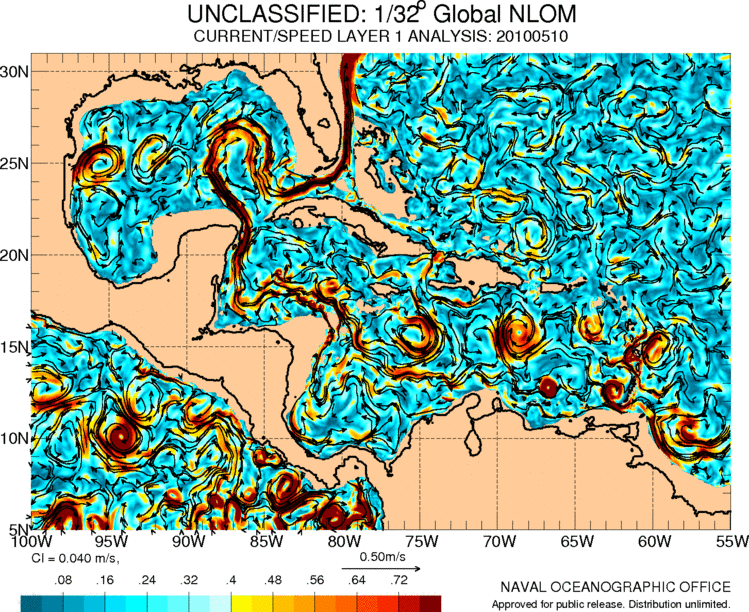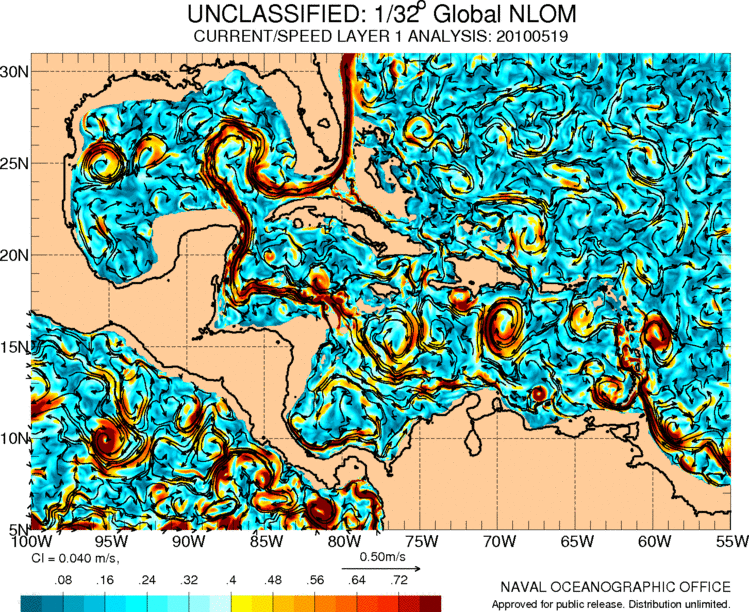
ID:(11487, 0)
Movimiento del X-15 Ben Franklin
Imagen
En 1969 el sumergible X-15 Ben Franklin del explorador Jacques Piccard se dejo arrastrar por la corriente del golfo. Floto para ello en una profundidad que correspondía a la flotación neutra (entre 180 a 610 m) y recorrió 2324 km:
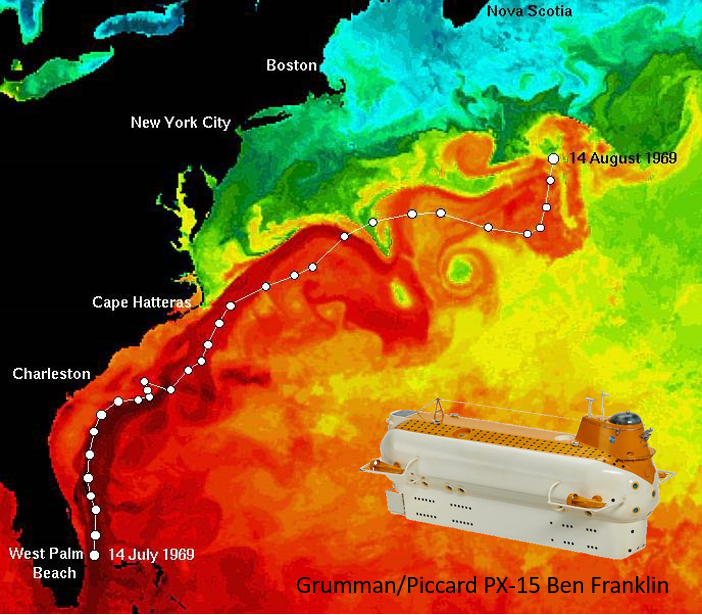
ID:(11488, 0)
Drifter (boya libre)
Concepto
Para estudiar corrientes oceánicas en la capa superior midiendo posición (y con ello velocidad), radiación, temperatura y salinidad, se usan boyas libres que se denominan drifters o drifters langrangianos:
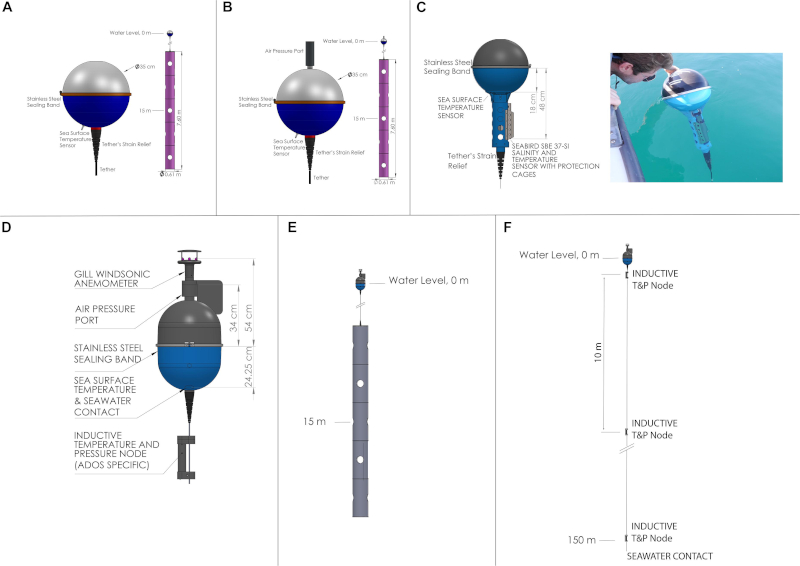
ID:(11498, 0)
Distribución de Drifters (boya libre)
Concepto
Existen distintos programas que han distribuido drifers sobre todos los océanos para monitorear el flujo en el océano. Un ejemplo es el Global Drifter Program (GDP) que presenta la siguiente distribución:
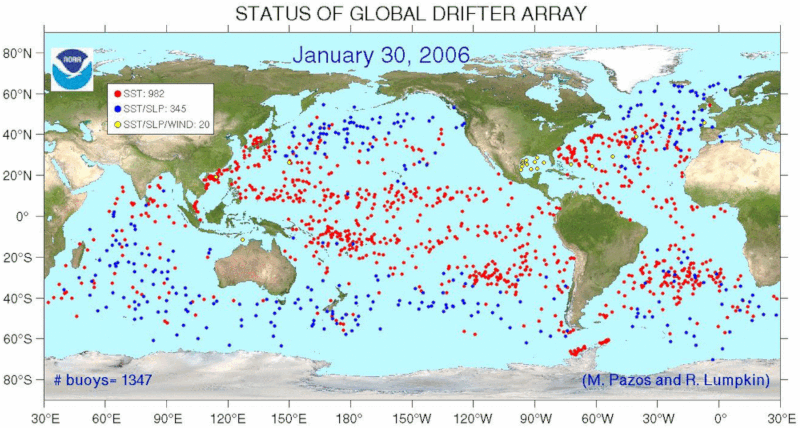
ID:(11499, 0)
Rotación como traslación, posición
Concepto
El movimiento de rotación se puede expresar como desplazamiento en las direcciones x e y con valores de la distancia del objeto del centro del vórtice ($r$)8519 y el angulo del objeto en el vórtice ($\theta_w$)8516, respectivamente. Con las coordenadas la posición x del centro vórtice ($X$)8506 y la posición y del centro vórtice ($Y$)8507, se obtiene que la posición x del objeto ($x$)8508 es:
| $ x = X + r \cos \theta_w$ |
y para la posición y del objeto ($y$)8509:
| $ y = Y + r \sin \theta_w$ |
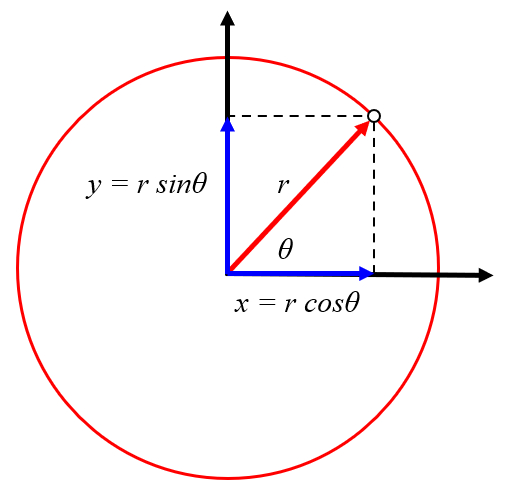
ID:(11490, 0)
Rotación como traslación, velocidad
Imagen
El movimiento de rotación puede expresarse como desplazamiento en las direcciones x e y, con velocidades de coordenada x de la velocidad del drifter ($u$)9913 y coordenada y de la velocidad del drifter ($v$)9914, respectivamente. Con las coordenadas la velocidad x del centro vórtice ($U$)8510 y la velocidad y del centro vórtice ($V$)8511, se obtiene que coordenada x de la velocidad del drifter ($u$)9913 es:
| $ u = U - r \omega \sin \theta_w $ |
y para coordenada y de la velocidad del drifter ($v$)9914:
| $ v = V + r \omega \cos \theta_w $ |
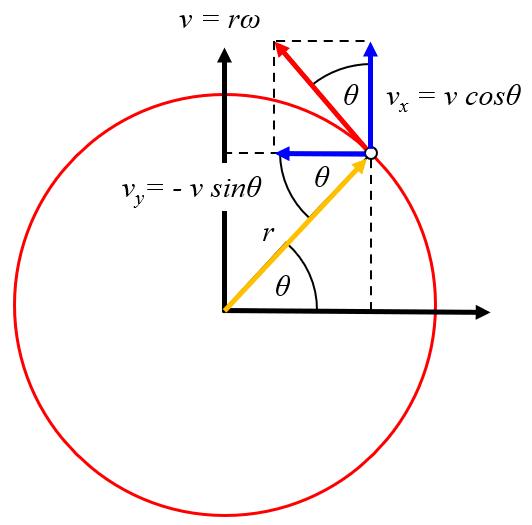
ID:(11489, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ r ^2=( X - x )^2 + ( Y - y )^2 $
r ^2=( X - x )^2 + ( Y - y )^2
$ \theta_w = \theta_0 + \omega t $
theta_w = theta_0 + omega * t
$ u = U - r \omega \sin \theta_w $
u = U - r * omega * sin( theta_w )
$ v_t = r \omega $
v = r * omega
$ v = V + r \omega \cos \theta_w $
v = V + r * omega * cos( theta_w )
$ x = X + r \cos \theta_w$
x = X + r * cos( theta_w )
$ X = X_0 + U t $
X = X_0 + U * t
$ y = Y + r \sin \theta_w$
y = Y + r * sin( theta_w )
$ Y = Y_0 + V t $
Y = Y_0 + V * t
ID:(15445, 0)
Posición x del vertice
Ecuación
El vórtice se traslada en la dirección $x$ con una velocidad x del centro vórtice ($U$)8510,1 constante, desde una posición inicial x ($X_0$)8514,1 alcanzando en el tiempo desde el inicio del rastreo ($t$)8520 en $x$
la posición x del centro vórtice ($X$)8506:
| $ X = X_0 + U t $ |
ID:(11495, 0)
Posición y del vortice
Ecuación
El vórtice se traslada en la dirección $y$ con una velocidad y del centro vórtice ($V$)8511,1 constante, desde una posición inicial y ($Y_0$)8515,1 alcanzando en el tiempo desde el inicio del rastreo ($t$)8520 en $y$ La posición y del centro vórtice ($Y$)8507:
| $ Y = Y_0 + V t $ |
ID:(11496, 0)
Angulo $\theta$ del vortice
Ecuación
El vórtice gira constantemente a una velocidad angular del objeto en el vórtice ($\omega$)8518,1, partiendo desde un angulo inicial del objeto en el vórtice ($\theta_0$)8517,1 y llegando en el tiempo desde el inicio del rastreo ($t$)8520 a un angulo del objeto en el vórtice ($\theta_w$)8516,1:
| $ \theta_w = \theta_0 + \omega t $ |
ID:(11497, 0)
Distancia del objeto al centro del vórtice
Ecuación
La distancia entre el objeto en la posición x del objeto ($x$)8508 y la posición y del objeto ($y$)8509 y el centro del vórtice en la posición x del centro vórtice ($X$)8506 y la posición y del centro vórtice ($Y$)8507 se puede calcular con el teorema de Pitágoras, lo que da como resultado la distancia del objeto del centro del vórtice ($r$)8519:
| $ r ^2=( X - x )^2 + ( Y - y )^2 $ |
ID:(11500, 0)
Posición x de cuerpo que rota
Ecuación
Si un cuerpo rota en un angulo el angulo del objeto en el vórtice ($\theta_w$)8516 a una distancia la distancia del objeto del centro del vórtice ($r$)8519 de un centro que esta en la posición la posición x del centro vórtice ($X$)8506 se tendra una posición x del objeto ($x$)8508,1:
| $ x = X + r \cos \theta_w$ |
ID:(11491, 0)
Posición y de cuerpo que rota
Ecuación
Si un cuerpo rota en un angulo el angulo del objeto en el vórtice ($\theta_w$)8516 a una distancia la distancia del objeto del centro del vórtice ($r$)8519 de un centro que esta en la posición la posición y del centro vórtice ($Y$)8507 se tendra una posición y del objeto ($y$)8509,1:
| $ y = Y + r \sin \theta_w$ |
ID:(11492, 0)
Velocidad y velocidad angular
Ecuación
Si dividimos la relación entre la distancia recorrida en un tiempo ($\Delta s$)6025 y el radio ($r$)9894 por la variación del angulo ($\Delta\theta$)6066,
| $ \Delta s=r \Delta\theta $ |
y luego dividimos eso por el tiempo transcurrido ($\Delta t$)5103, obtenemos la relación que nos permite calcular la velocidad ($v$)6029 a lo largo de la órbita, conocida como velocidad tangencial, que es igual a la velocidad angular ($\omega$)6068:
| $ v_t = r \omega $ |
| $ v = r \omega $ |
Como la velocidad media ($\bar{v}$)5268 es con la distancia recorrida en un tiempo ($\Delta s$)6025 y el tiempo transcurrido ($\Delta t$)5103, igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
y con la distancia recorrida en un tiempo ($\Delta s$)6025 expresado como arco de un círculo, y el radio ($r$)9894 y la variación del angulo ($\Delta\theta$)6066 son
| $ \Delta s=r \Delta\theta $ |
y la definición de la velocidad angular media ($\bar{\omega}$)9943 es
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
entonces,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como la relación es general, se puede aplicar para valores instantáneos, lo que resulta en
| $ v = r \omega $ |
.
ID:(3233, 0)
Velocidad x de cuerpo que rota
Ecuación
Dado que el vórtice rota a la velocidad angular del objeto en el vórtice ($\omega$)8518 y se encuentra a una distancia del objeto del centro del vórtice ($r$)8519,1 de su centro, el objeto se desplaza a una velocidad tangencial del drifter ($v_t$)10336,1:
| $ v_t = r \omega $ |
Si un cuerpo está a un angulo del objeto en el vórtice ($\theta_w$)8516,1 y la velocidad en la dirección $x$ es la velocidad x del centro vórtice ($U$)8510, entonces coordenada x de la velocidad del drifter ($u$)9913 es:
| $ u = U - r \omega \sin \theta_w $ |
ID:(11493, 0)
Velocidad y de cuerpo que rota
Ecuación
Dado que el vórtice rota a la velocidad angular del objeto en el vórtice ($\omega$)8518 y se encuentra a una distancia del objeto del centro del vórtice ($r$)8519,1 de su centro, el objeto se desplaza a una velocidad tangencial del drifter ($v_t$)10336,1:
| $ v_t = r \omega $ |
Si un cuerpo está a un angulo del objeto en el vórtice ($\theta_w$)8516,1 y la velocidad en la dirección $y$ es la velocidad y del centro vórtice ($V$)8511, entonces coordenada y de la velocidad del drifter ($v$)9914 es:
| $ v = V + r \omega \cos \theta_w $ |
ID:(11494, 0)