Usuario:
Movimiento en bordes costeros
Storyboard 
En el borde costero la fuerza de Coriolis puede llevar a circulación que arrastra material rico en nutrientes hacia la superficie (transporte de Ekman).
ID:(1578, 0)
Transporte de Ekman
Concepto
Cuando existen corrientes en dirección del ecuador en los lados oeste en bordes continentales, la ecuación de Coriolis para el plano con
| $ a_{s,y} = - f v_x $ |
implica que existe una corriente que se aleja de la costa. Esto genera una corriente que lleva aguas frías ricas en nutrientes a la superficie:
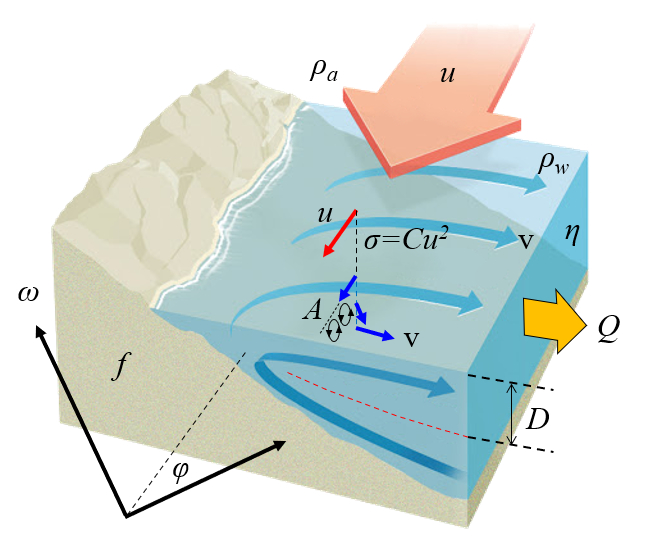
Este transporte se denomina el transporte de Ekman.
ID:(11679, 0)
Caracterización de las capas del océano
Imagen
El transporte de Ekman lleva a que se desplacen las fronteras que existen entre las capas superficiales y las mas profundas en el océano. Estas se caracterizan por cambios bruscos de parámetros en función de la temperatura. En particular se tienen cambios en:
• Temperatura (termoclina)
• Salinidad (haloclina)
• Densidad (picnoclina)
ID:(11684, 0)
Transporte inverso de Ekman
Imagen
Si se invierte el sentido del viento para el transporte de Ekman se tiene el proceso inverso (si
En este caso se tiene que con la velocidad hacia los polos resulta
| $ a_{s,y} = - f v_x $ |
Esto implica que existe una corriente que va hacia la costa evitando que los nutrientes lleguen a la superficie:
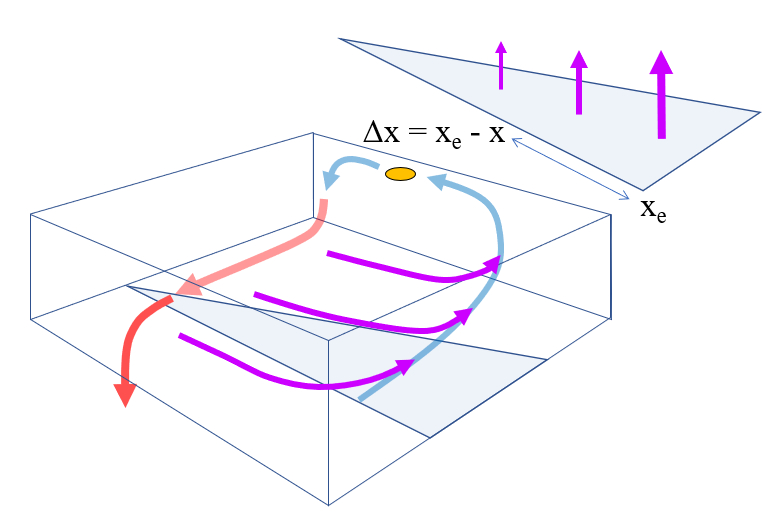
ID:(11680, 0)
Zonas de surgencia (upwelling)
Imagen
Existen distintas zonas en el mundo en donde por vientos, ya sea en forma permanente o estacional, existe surgencia. Esto lleva a que en estos lugares las corrientes que van en dirección de la costa arrastran aguas frias ricas en vida en dirección de la superficie con lo que se favorece la vida en la superficie.
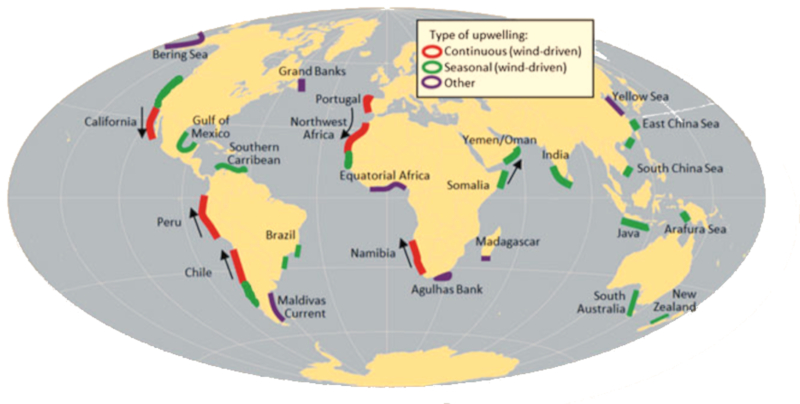
ID:(11700, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ D_E =\sqrt{\displaystyle\frac{2 \pi A_z }{ f }}$
D_E =sqrt( 2 * pi * A_z / f )
$ Q = D_E u_e $
Q = D_E * u_e
$ \tau_w = \rho_a C_D U ^2$
tau_w = rho_a * C_D * U ^2
$ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$
u_e = tau_w /( f * rho_w * D_E )
ID:(15443, 0)
Tensión superficial generada por el viento
Ecuación
La densidad de energía del viento es una función de la densidad del aire ($\rho_a$)8606 y la velocidad del viento ($U$)8609 de la forma
$\displaystyle\frac{1}{2}\rho_aU^2$
Si se considera que solo una fracción de la energía es transferida se puede modelar la tensión generada por el viento ($\tau_w$)8603 como la densidad de energía multiplicada por un factor la coeficiente de arrastre ($C_D$)8604:
| $ \tau_w = \rho_a C_D U ^2$ |
ID:(11718, 0)
Profundidad de Ekman
Ecuación
La tensión en la superficie del océano generada por el viento es transmitida a las profundidades mediante vórtices, lo que genera el arrastre de la masa de agua. La profundidad del agua, o la profundidad de Ekman ($D_E$)8607, que se puede arrastrar, depende de cómo la energía se difunde a capas más profundas, lo que corresponde a la viscosidad de remolinos para mezcla vertical ($A_z$)8610. Es, con el factor de Coriolis ($f$)8600, igual a:
| $ D_E =\sqrt{\displaystyle\frac{2 \pi A_z }{ f }}$ |
ID:(11670, 0)
Velocidad el flujo de Ekman
Ecuación
La la tensión generada por el viento ($\tau_w$)8603 generada por el viento lleva a la velocidad superficial del océano, o la velocidad de Ekman ($u_e$)8608, que a su vez, mediante la fuerza de Coriolis representada por el el factor de Coriolis ($f$)8600, genera el transporte de Ekman. Este es, con la densidad del agua marína ($\rho$)8605 y la profundidad de Ekman ($D_E$)8607:
| $ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$ |
Con la tensión generada por el viento ($\tau_w$)8603 sobre la superficie $S$ del océano se genera una fuerza
$F = \sigma_w S$
que actúa sobre la masa $m$, que se calcula a partir de la densidad del agua marína ($\rho$)8605, la profundidad de Ekman ($D_E$)8607 y la superficie $S$, mediante
$m = \rho_w S D_E$
Como la aceleración $a$ es generada por la fuerza de Coriolis con la velocidad de Ekman ($u_e$)8608,
$a = \displaystyle\frac{F}{m} =\displaystyle\frac{\sigma_w S}{\rho_w D_E S} = \displaystyle\frac{\sigma_w}{\rho_w D_E} = f u_e$
por lo que resulta:
| $ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$ |
ID:(11701, 0)
Transporte de Ekman
Ecuación
Con la velocidad de Ekman ($u_e$)8608 y la profundidad de Ekman ($D_E$)8607, se puede estimar el volumen transportado, o el transporte de Ekman ($Q$)8611:
| $ Q = D_E u_e $ |
ID:(11702, 0)