Utilisateur: 
Mouvement océanique, dériveurs
Storyboard 
Le mouvement à la surface des océans résulte de l'interaction avec l'atmosphère et est conditionné par les courants plus profonds (de plus de 15 mètres). Dans une première approche, il peut être considéré comme un flux à vitesse constante avec des tourbillons stables ou entraînés par celui-ci.
ID:(1519, 0)
Mécanismes
Iframe
Mécanismes
ID:(15449, 0)
Rotation comme translation, position
Concept
Le mouvement de rotation peut être exprimé comme un déplacement dans les directions x et y avec des valeurs de a distance de l'objet au centre du vortex (r) et le angle de l'objet dans le vortex (\theta_w), respectivement. Avec les coordonnées a position x du centre du vortex (X) et a position y du centre du vortex (Y), nous obtenons que a position x de l'objet (x) est :
| x = X + r \cos \theta_w |
et pour a position y de l'objet (y) :
| y = Y + r \sin \theta_w |
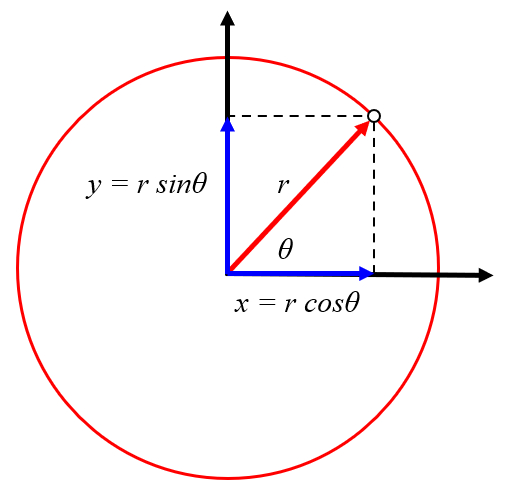
ID:(11490, 0)
Rotation comme translation, vitesse
Image
Le mouvement de rotation peut être exprimé comme un déplacement dans les directions x et y avec des vitesses de ($$) et ($$), respectivement. Avec les coordonnées a vitesse x du centre du vortex (U) et a vitesse y du centre du vortex (V), nous obtenons que ($$) est :
| u = U - r \omega \sin \theta_w |
| v = V + r \omega \cos \theta_w |
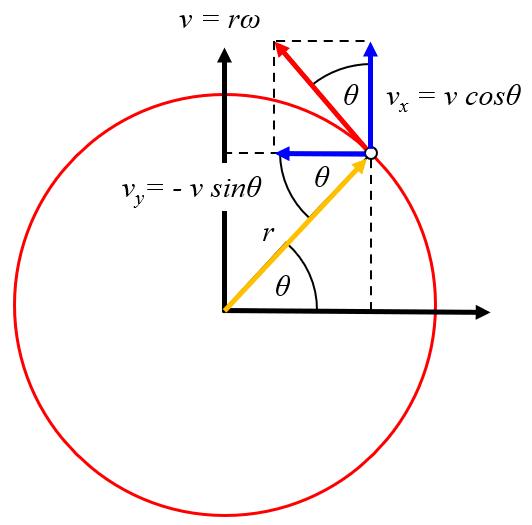
ID:(11489, 0)
Modèle
Top
Paramètres
Variables
Calculs
à 
, puis, sélectionnez la variable: 
à 
Calculs
Calculs
Variable 
Donnée Calculer 
Cible : Équation À utiliser 
Équations
r ^2=( X - x )^2 + ( Y - y )^2
r ^2=( X - x )^2 + ( Y - y )^2
\theta_w = \theta_0 + \omega t
theta_w = theta_0 + omega * t
u = U - r \omega \sin \theta_w
u = U - r * omega * sin( theta_w )
v_t = r \omega
v = r * omega
v = V + r \omega \cos \theta_w
v = V + r * omega * cos( theta_w )
x = X + r \cos \theta_w
x = X + r * cos( theta_w )
X = X_0 + U t
X = X_0 + U * t
y = Y + r \sin \theta_w
y = Y + r * sin( theta_w )
Y = Y_0 + V t
Y = Y_0 + V * t
ID:(15445, 0)
Position du sommet x
Équation
Le vortex se déplace dans la direction x avec une constante de a vitesse x du centre du vortex (U) à partir de une position de départ x (X_0), atteignant en le temps écoulé depuis le début du suivi (t) A position x du centre du vortex (X):
| X = X_0 + U t |
ID:(11495, 0)
Position du sommet y
Équation
Le vortex se déplace dans la direction y avec une constante de une vitesse y du centre du vortex (V), à partir de une position de départ y (Y_0) atteignant le temps écoulé depuis le début du suivi (t) en y A position y du centre du vortex (Y) :
| Y = Y_0 + V t |
ID:(11496, 0)
Angle \theta du vortex
Équation
Le vortex tourne de manière constante à ($$), en partant de un angle initial de l'objet dans le vortex (\theta_0) et atteignant le temps écoulé depuis le début du suivi (t) à Un angle de l'objet dans le vortex (\theta_w):
| \theta_w = \theta_0 + \omega t |
ID:(11497, 0)
Distance de l'objet au centre du vortex
Équation
La distance entre l'objet en a position x de l'objet (x) et a position y de l'objet (y) et le centre des vortex en a position x du centre du vortex (X) et a position y du centre du vortex (Y) peut être calculée en utilisant le théorème de Pythagore, ce qui donne a distance de l'objet au centre du vortex (r) :
| r ^2=( X - x )^2 + ( Y - y )^2 |
ID:(11500, 0)
Position x du corps en rotation
Équation
Si un corps tourne à un angle de le angle de l'objet dans le vortex (\theta_w) à une distance de a distance de l'objet au centre du vortex (r) d'un centre situé à la position a position x du centre du vortex (X), le résultat est une position x de l'objet (x):
| x = X + r \cos \theta_w |
ID:(11491, 0)
Position y du corps en rotation
Équation
Si un corps tourne à un angle de le angle de l'objet dans le vortex (\theta_w) à une distance de a distance de l'objet au centre du vortex (r) d'un centre situé à la position a position y du centre du vortex (Y), le résultat sera une position y de l'objet (y):
| y = Y + r \sin \theta_w |
ID:(11492, 0)
Vitesse et vitesse angulaire
Équation
Si nous divisons la relation entre a distance parcourue en un temps (\Delta s) et le radio (r) par a variation d'angle (\Delta\theta),
| \Delta s=r \Delta\theta |
et puis la divisons par le temps écoulé (\Delta t), nous obtenons la relation qui nous permet de calculer a vitesse (v) le long de l'orbite, connue sous le nom de vitesse tangentielle, qui est associée à A vitesse angulaire (\omega):
| v_t = r \omega |
| v = r \omega |
Comme a vitesse moyenne (\bar{v}) est avec a distance parcourue en un temps (\Delta s) et le temps écoulé (\Delta t), égal à
| \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t } |
et avec a distance parcourue en un temps (\Delta s) exprimé comme un arc de cercle, et le radio (r) et a variation d'angle (\Delta\theta) sont
| \Delta s=r \Delta\theta |
et la définition de a vitesse angulaire moyenne (\bar{\omega}) est
| \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t } |
alors,
v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega
Comme la relation est générale, elle peut être appliquée pour des valeurs instantanées, ce qui donne
| v = r \omega |
ID:(3233, 0)
Vitesse x du corps en rotation
Équation
Étant donné que le vortex tourne à ($$) et est situé à Une distance de l'objet au centre du vortex (r) de son centre, l'objet se déplace à Une vitesse tangentielle du dériveur (v_t):
Si un corps se trouve à Un angle de l'objet dans le vortex (\theta_w) et que la vitesse dans la direction x est de a vitesse x du centre du vortex (U), alors ($$) est:
| u = U - r \omega \sin \theta_w |
ID:(11493, 0)
Vitesse y du corps en rotation
Équation
Étant donné que le vortex tourne à ($$) et est situé à Une distance de l'objet au centre du vortex (r) de son centre, l'objet se déplace à Une vitesse tangentielle du dériveur (v_t) :
Si un corps est à Un angle de l'objet dans le vortex (\theta_w) et que la vitesse dans la direction y est a vitesse y du centre du vortex (V), alors ($$) est :
| v = V + r \omega \cos \theta_w |
ID:(11494, 0)