Usuario:
Movimiento de los océanos, circulación
Storyboard 
Las corrientes marinas son generadas por vientos y cambios de densidad del agua. La fuerza de Coriolis afecta estos vórtices deformando e influenciando la profundidad que alcanzan.
ID:(1560, 0)
Generación de corrientes
Imagen
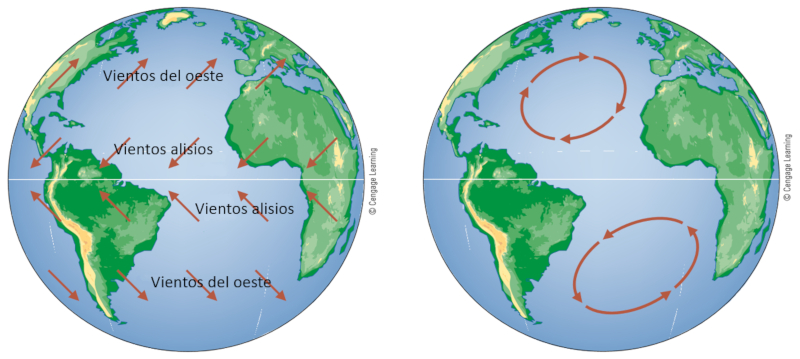
Las corrientes marinas son ageneradas por los vientos de superficie y fluctuaciones de la densidad del agua. El sentido de la circulación es definido por los vientos del oeste (westerlies) y vientos alisios (trade winds), generando circulaciones negativas en el hemisferio norte y positivas en el hemisferio sur.
ID:(11687, 0)
Mezcla de calor por efecto de los vórtices
Imagen
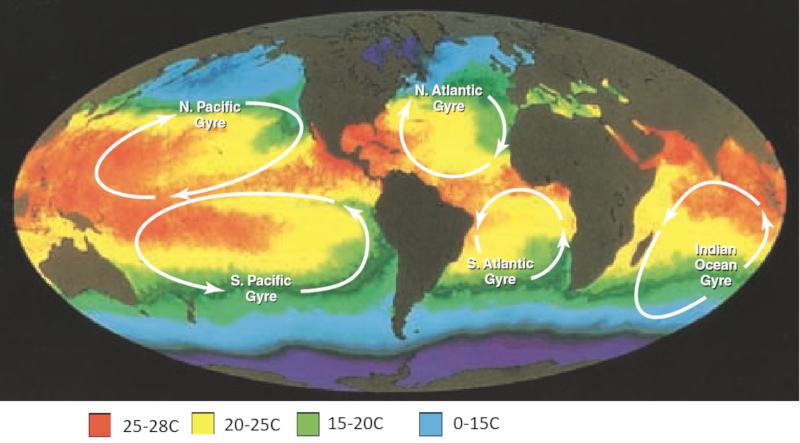
La radiación solar caliente ante todo el océano en latitudes próximas al ecuador. Los vórtices sin embargo pueden arrastrar aguas cálidas hacia los polos y de los polos hacia el ecuador mezclando las aguas cálidas con las frías en las zonas polares.
ID:(11686, 0)
Circulación superficial en los océanos
Imagen
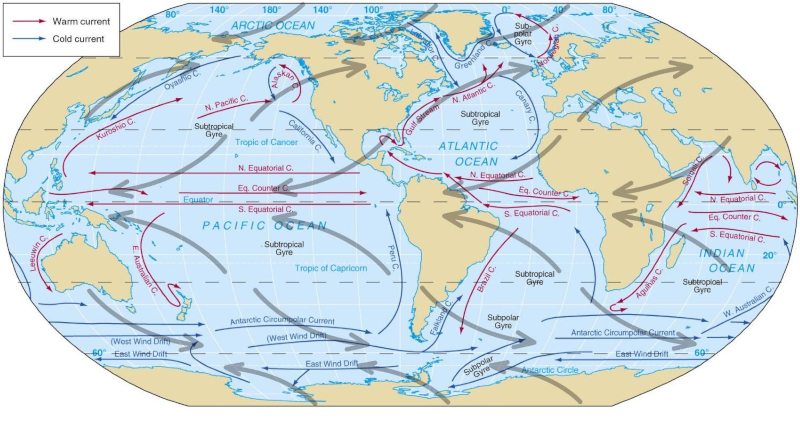
La circulación inducida por los vientos en la atmósfera genera cinco vórtices mayores: dos en el pacifico, dos en el atlántico y uno en el mar indico.
Como anticipado por la ley de Coriolis estos giran en el hemisferio norte en el sentido negativo (como las manecillas del reloj) y positivo en el hemisferio sur (contra las manecillas del reloj).
Se clasifican de frío y caliente según la temperatura que van adquiriendo en las zonas ecuatoriales y polares.
ID:(11676, 0)
Deformación de los vórtices por la fuerza de Coriolis
Imagen
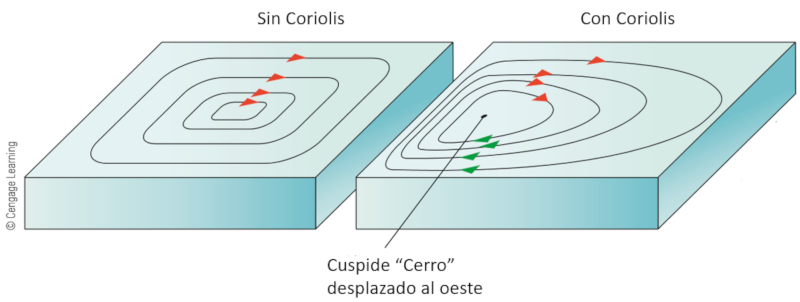
Como la fuerza de Coriolis es nula en el ecuador y crece en dirección de latitudes mayores las corrientes que viajan desde el ecuador hacia los polos tienden a ser angostas. Sin embargo, a medida que se aproximan a los polos, las fuerzas de Coriolis tienden a desviarlas hacia el lado este (hemisferio norte)/oeste (hemisferio sur) de la corriente llevando a un ensanchamiento de la corriente.
Por ello las corrientes que regresan en dirección del ecuador tienden a ser mas anchas, existiendo distorsiones por islas y superficies muy extensas (pacifico).
El centro del vórtice se desplaza con ello hacia el oeste (hemisferio norte) o este (hemisferio sur).
ID:(11688, 0)
Formación de vórtices menores
Imagen
En situaciones en que corrientes de distinta temperatura interactuan se forman vórtices mediante la separación de áreas de la corriente principal que por el movimiento relativo de las corrientes giran. Estos vórtices presentan inercia que hace que tiendan a mantener su forma y viajen en una de las corrientes largos recorridos antes de desarmarse.
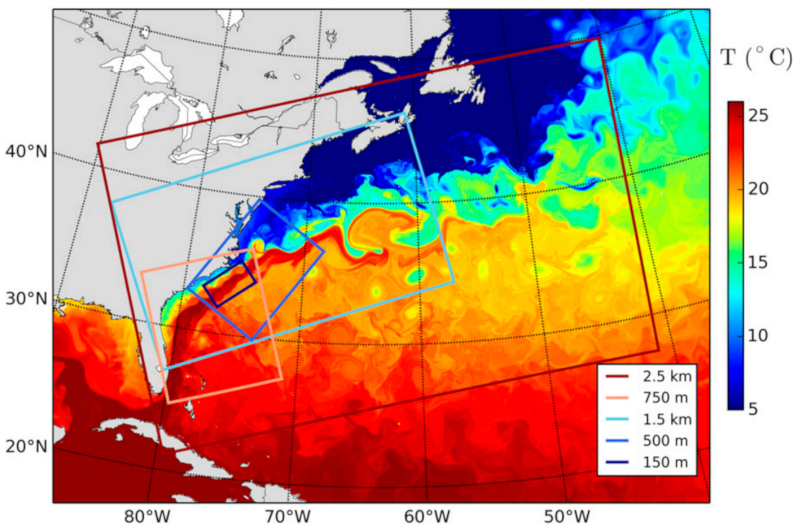
ID:(11677, 0)
Detalle de la formación de vórtices menores
Imagen
En estas laminas se muestra la formación de vórtices menores en mas detalle:
• dos corrientes interactuando
• por fluctuaciones se forman protuberancias que invaden el área de la otra corriente
• áreas comienzan a girar
• por inercia mantienen la forma e incursionan en la otra corriente
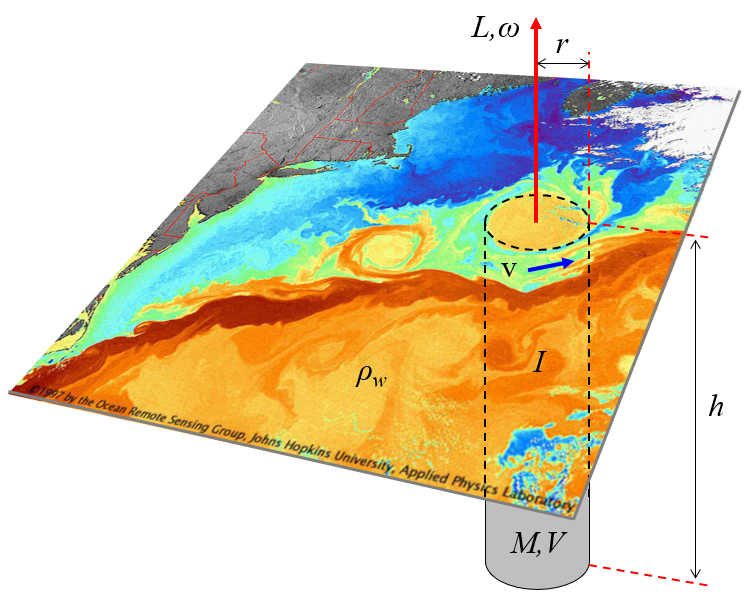
ID:(11678, 0)
Circulación de Langmuir hacia/desde las profundidades
Imagen
Al simplificar las ecuaciones de la ley de Coriolis se obvian movimientos fuera del plano. Sin embargo para movimientos de masas de agua estos si pueden existir y generar aceleraciones hacia la superficie que con es:
| $ a_{c,z} = 2 \omega v_x \cos \varphi$ |
Si se suma a esto la tendencia de que con movimientos hacia el norte en el hemisferio norte existen desplazamientos en la superficie hacia el este se generan circulaciones dentro de una capa de algunos metros. Estas forman verdaderas 'trompas' que se localizan en forma paralela y se van alternando en el sentido de rotación. En los puntos de convergencia se pueden acumular algas y basura creando largas lineas de objetos que flotan.
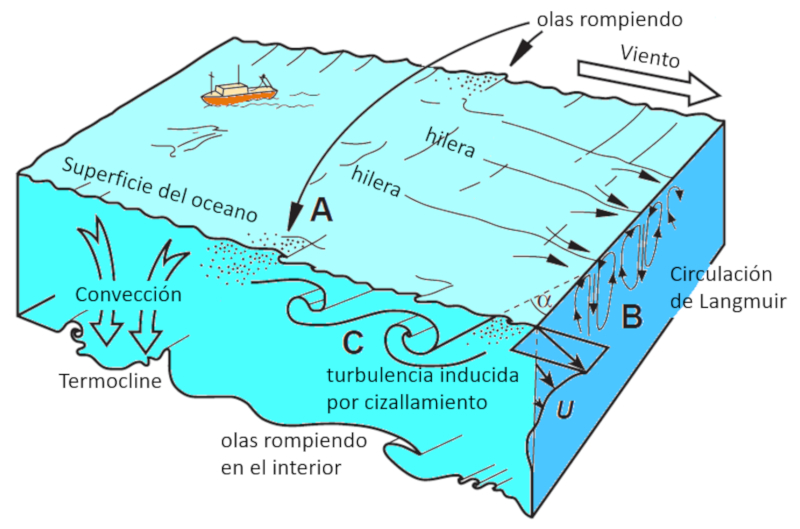
ID:(11681, 0)
Circulación de Langmuir
Imagen
Vista desde el aire de circulaciones de Langmuir: zonas de convergencia forman depresiones y de divergencias forman protuberancias.
ID:(11682, 0)
Circulación de superficie y de profundidad
Imagen
La densidad del agua (efecto de salinidad) genera una parte del flujo se 'hunda' participando en lo que son las corrientes de profundad o 'afloren' y participen en las de superficie.
Como las corrientes de la profundidad no dependen de los vientos no están sujetas a la dinámica de la superficie que se separa por la fuerza de Coriolis en circulación separada por hemisferios.
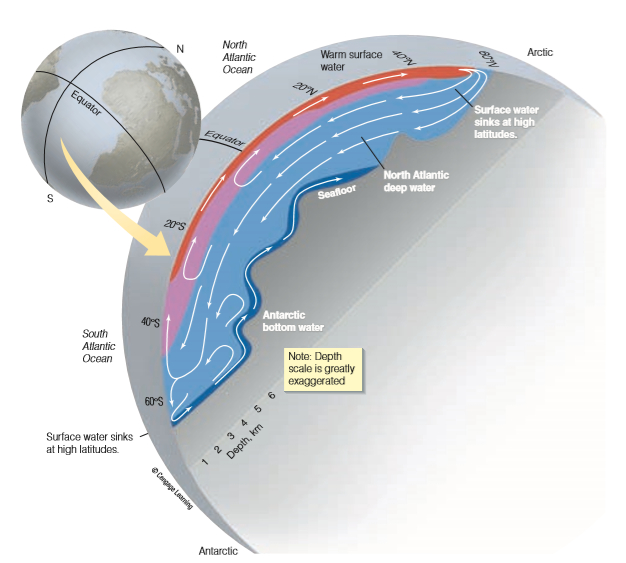
ID:(11690, 0)
Circulación profunda
Imagen
La corriente de profundidad se extiende sobre todo el globo extiendo también corrientes cálidas y frías. Esto depende del punto en que es alimentada por las corrientes superficiales:
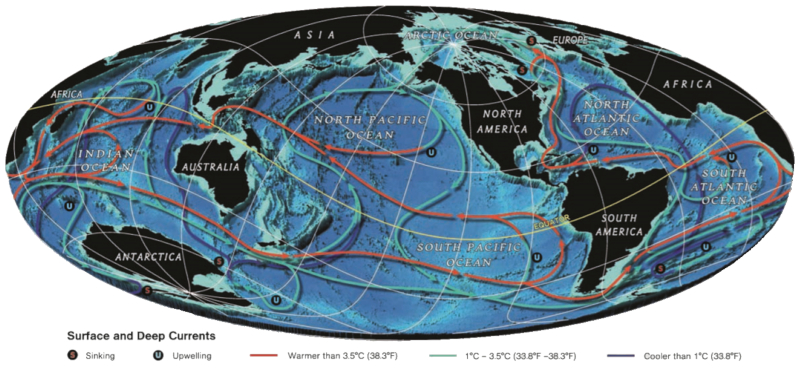
ID:(11691, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$ a_{s,x} = f v_y $
a_sx = f * v_y
$ a_{s,y} = - f v_x $
a_sy = - f * v_x
$ a_{s,z} = e v_x $
a_sz = e * v_x
$ e = 2 \omega \cos \varphi $
e = 2* omega * cos( phi )
$ f = 2 \omega \sin \varphi $
f = 2* omega * sin( phi )
ID:(15444, 0)
Factor de Coriolis
Ecuación
Para simplificar las ecuaciones, trabajamos con un factor de Coriolis ($f$)8600,1, que es una constante para el lugar físico, ya que incluye la velocidad angular del planeta ($\omega$)8595 para la Tierra y la latitud ($\varphi$)8596 para el lugar:
| $ f = 2 \omega \sin \varphi $ |
En el hemisferio sur, la latitud es negativa, y con ella 8600, lo que explica que los sistemas roten en dirección opuesta al hemisferio norte.
ID:(11697, 0)
Segundo factor de Coriolis
Ecuación
Para simplificar las ecuaciones, trabajamos con un segundo factor de Coriolis ($e$)10273,1, que es una constante para el lugar físico, ya que incluye la velocidad angular del planeta ($\omega$)8595 para la Tierra y la latitud ($\varphi$)8596 para el lugar:
| $ e = 2 \omega \cos \varphi $ |
ID:(15450, 0)
Aceleración de Coriolis en el plano, coordenada x
Ecuación
Como la aceleración de Coriolis en dirección x ($a_{c,x}$)8597 puede reescribirse con el factor de Coriolis ($f$)8600 y bajo la condición de que no hay movimiento vertical:
$v_z = 0$
Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección x ($a_{s,x}$)8601 es:
| $ a_{s,x} = f v_y $ |
Como la aceleración de Coriolis en dirección x ($a_{c,x}$)8597 se compone de la velocidad angular del planeta ($\omega$)8595, la latitud ($\varphi$)8596, la velocidad y del objeto ($v_y$)8513 y la velocidad z del objeto ($v_z$)8594:
| $ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$ |
y la definición de el factor de Coriolis ($f$)8600 es:
| $ f = 2 \omega \sin \varphi $ |
además de la restricción de un movimiento en la superficie en la que:
$v_z = 0$
esto lleva a que la aceleración de Coriolis en dirección x ($a_{c,x}$)8597 sea:
| $ a_{s,x} = f v_y $ |
ID:(11698, 0)
Aceleración de Coriolis en el plano, coordenada y
Ecuación
Como la aceleración de Coriolis en dirección x ($a_{c,x}$)8597 puede reescribirse con el factor de Coriolis ($f$)8600 y bajo la condición de que no hay movimiento vertical:
$v_z = 0$
Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección y ($a_{s,y}$)8602 es:
| $ a_{s,y} = - f v_x $ |
Como la aceleración de Coriolis en dirección y ($a_{c,y}$)8598 se compone de la velocidad angular del planeta ($\omega$)8595, la velocidad x del objeto ($v_x$)8512 y la latitud ($\varphi$)8596:
| $ a_{c,y} = -2 \omega v_x \sin \varphi$ |
y la definición de el factor de Coriolis ($f$)8600 es:
| $ f = 2 \omega \sin \varphi $ |
además de la restricción de un movimiento en la superficie en la que:
$v_z = 0$
esto lleva a que la aceleración de Coriolis en dirección y ($a_{c,y}$)8598 sea:
| $ a_{s,y} = - f v_x $ |
ID:(11699, 0)
Aceleración de Coriolis en el plano, coordenada z
Ecuación
Como la aceleración de Coriolis en dirección z ($a_{c,z}$)8599 puede reescribirse con el segundo factor de Coriolis ($e$)10273 y bajo la condición de que no hay movimiento vertical:
$v_z = 0$
Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección z ($a_{s,z}$)10274 es:
| $ a_{s,z} = e v_x $ |
Como la aceleración de Coriolis en dirección z ($a_{c,z}$)8599 se compone de la velocidad angular del planeta ($\omega$)8595, la velocidad x del objeto ($v_x$)8512 y la latitud ($\varphi$)8596:
| $ a_{c,z} = 2 \omega v_x \cos \varphi$ |
y la definición de el segundo factor de Coriolis ($e$)10273 es:
| $ e = 2 \omega \cos \varphi $ |
además de la restricción de un movimiento en la superficie en la que:
$v_z = 0$
esto lleva a que la aceleración de Coriolis en la superficie, en dirección z ($a_{s,z}$)10274 sea:
| $ a_{s,z} = e v_x $ |
ID:(15451, 0)