Ocean movement, drifters
Storyboard 
The movement on the surface of the oceans arises from the interaction with the atmosphere and is conditioned by the deeper currents (more than 15 meters). In a first approximation, it can be considered as a flow at a constant velocity with stable vortices or those dragged by it.
ID:(1519, 0)
Ocean movements
Video 
The movement of the ocean is generated on the surface by the movement of the air while in the depth by variations in density conditioned by temperature and salinity. Different effects are shown in the following NASA video:
ID:(11485, 0)
Gulf stream
Image 
One of the most important currents in the Atlantic Ocean is the so-called Gulf Stream. It carries warm waters from the Caribbean to Europe, contributing to a milder climate in this area:
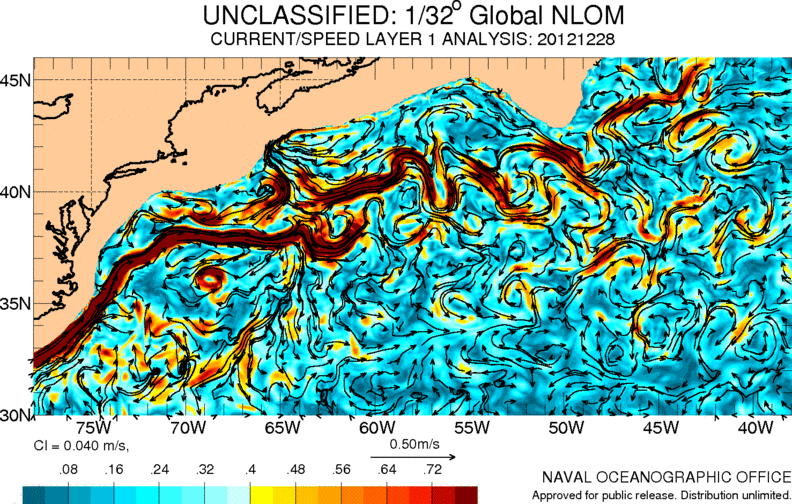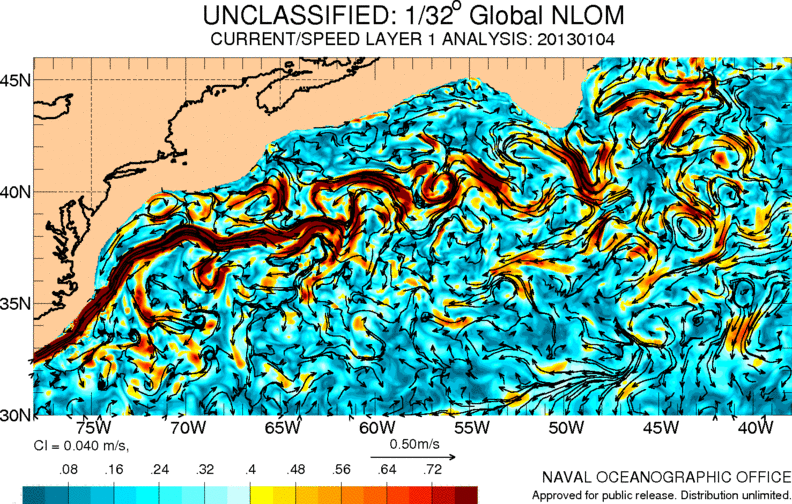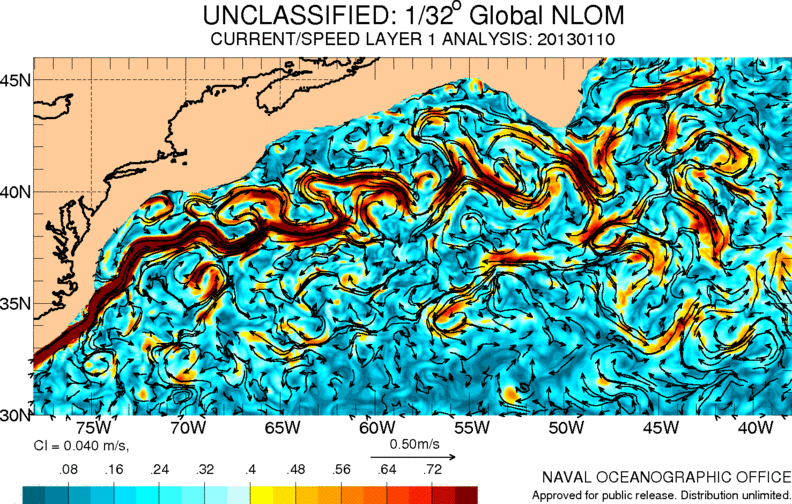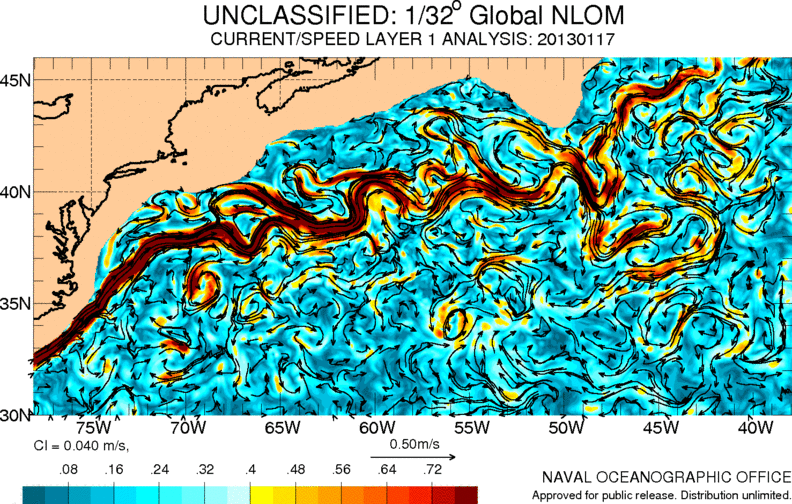
ID:(11486, 0)
Currents in central america and the caribbean
Image 
The Gulf Stream originates from the Caribbean where there is also a series of circulation associated with the movements of the air masses in the region:
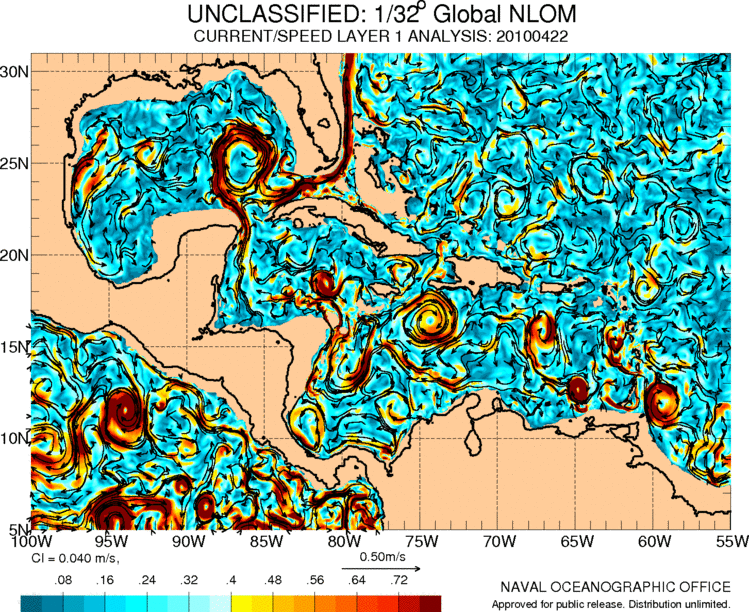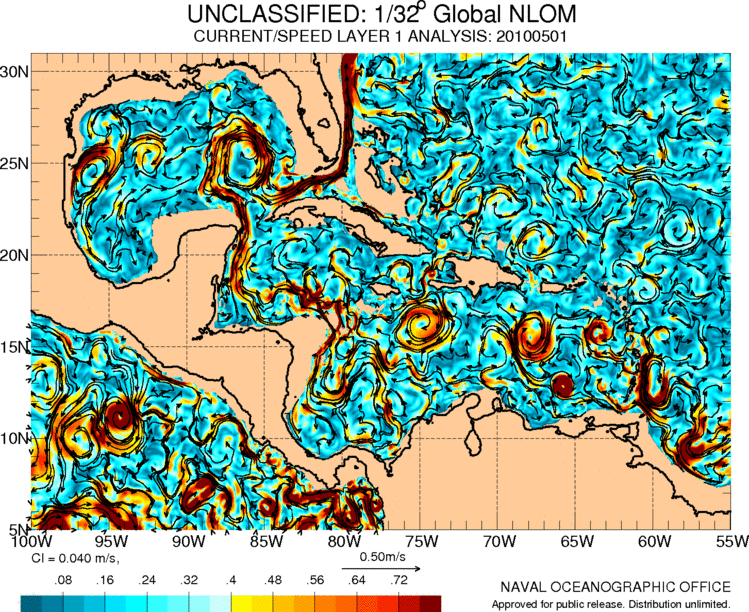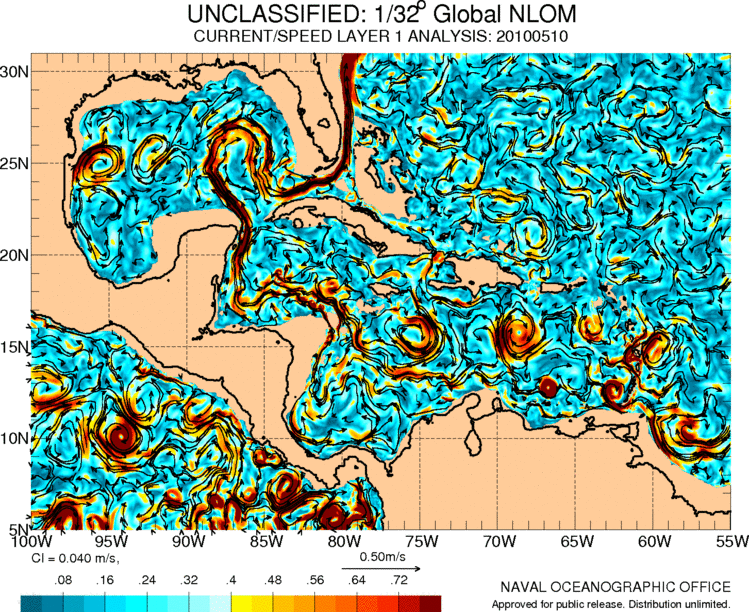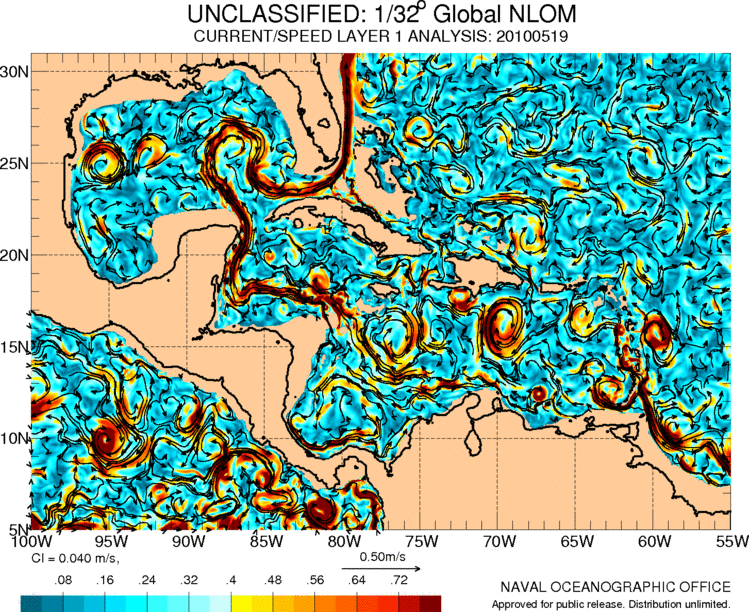
ID:(11487, 0)
X-15 Ben Franklin movement
Image 
In 1969 explorer Jacques Piccard's X-15 Ben Franklin submersible was swept away by the Gulf Stream. I float for this at a depth that corresponded to neutral flotation (between 180 to 610 m) and covered 2324 km:

ID:(11488, 0)
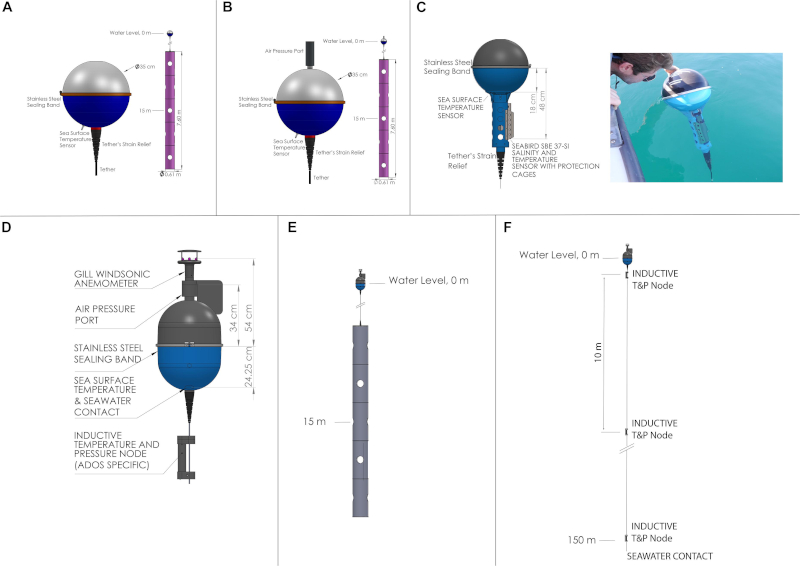
Drifter (free buoy)
Concept 
To study ocean currents in the upper layer by measuring position (and with it speed), radiation, temperature and salinity, free buoys are used, which are called langrangian drifters or drifters:
ID:(11498, 0)
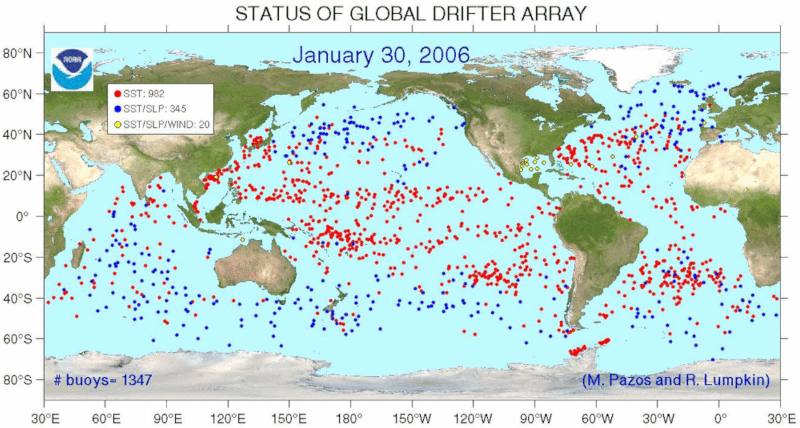
Drifters distribution (free buoy)
Concept 
There are different programs that have distributed drifers over all the oceans to monitor the flow in the ocean. An example is the Global Drifter Program (GDP) that presents the following distribution:
ID:(11499, 0)
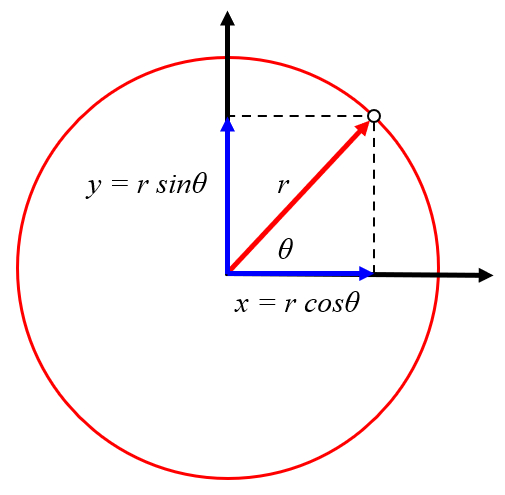
Rotation and Traslation, position
Concept 
The rotational movement can be expressed as displacement in the x and y directions with values of the object distance from vortex center (r) and the object angle in the vortex (\theta_w), respectively. With coordinates the position x of the vortex center (X) and the position y of the vortex center (Y), we obtain that the position x of the object (x) is:
| x = X + r \cos \theta_w |
and for the position y of the object (y):
| y = Y + r \sin \theta_w |
ID:(11490, 0)
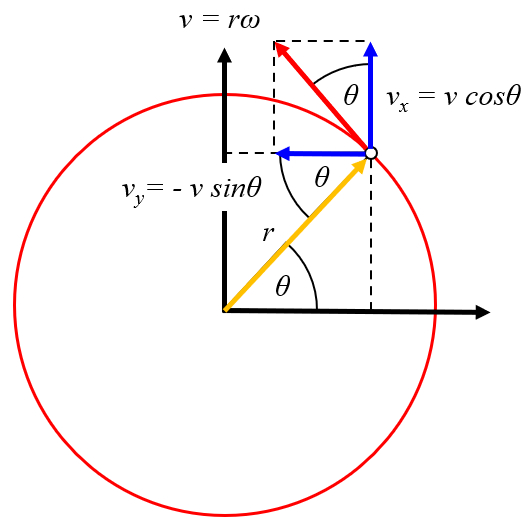
Rotation and Traslation, speed
Image 
The rotational movement can be expressed as displacement in the x and y directions with velocities of coordenada x de la velocidad del drifter (u) and coordenada y de la velocidad del drifter (v), respectively. With coordinates the speed x of the vortex center (U) and the speed y of the vortex center (V), we obtain that coordenada x de la velocidad del drifter (u) is:
| u = U - r \omega \sin \theta_w |
and for coordenada y de la velocidad del drifter (v):
| v = V + r \omega \cos \theta_w |
ID:(11489, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
r ^2=( X - x )^2 + ( Y - y )^2
r ^2=( X - x )^2 + ( Y - y )^2
\theta_w = \theta_0 + \omega t
theta_w = theta_0 + omega * t
u = U - r \omega \sin \theta_w
u = U - r * omega * sin( theta_w )
v_t = r \omega
v = r * omega
v = V + r \omega \cos \theta_w
v = V + r * omega * cos( theta_w )
x = X + r \cos \theta_w
x = X + r * cos( theta_w )
X = X_0 + U t
X = X_0 + U * t
y = Y + r \sin \theta_w
y = Y + r * sin( theta_w )
Y = Y_0 + V t
Y = Y_0 + V * t
ID:(15445, 0)
Position x of the vortex
Equation 
The vortex moves in the x direction with a constant of ($$), from ($$) reaching the time from start of trace (t) in x The position x of the vortex center (X):
ID:(11495, 0)
Position y of the vortex
Equation 
The vortex moves in the y direction with a constant of ($$), from ($$) reaching the time from start of trace (t) in y The position y of the vortex center (Y):
ID:(11496, 0)
Angle \theta of the vortice
Equation 
The vortex rotates steadily at ($$), starting from ($$) and reaching the time from start of trace (t) at ($$):
ID:(11497, 0)
Distance of the object to the center of the vortex
Equation 
The distance between the object at the position x of the object (x) and the position y of the object (y) and the center of the vortices at the position x of the vortex center (X) and the position y of the vortex center (Y) can be calculated using the Pythagorean theorem, resulting in the object distance from vortex center (r):
ID:(11500, 0)
X position of rotating body
Equation 
If a body rotates at an angle of the object angle in the vortex (\theta_w) at a distance of the object distance from vortex center (r) from a center positioned at the position x of the vortex center (X), the result is ($$):
ID:(11491, 0)
Y position of rotating body
Equation 
If a body rotates at an angle of the object angle in the vortex (\theta_w) at a distance of the object distance from vortex center (r) from a center located at position the position y of the vortex center (Y), the result will be ($$):
ID:(11492, 0)
Speed and angular speed
Equation 
If we divide the relationship between the distance traveled in a time (\Delta s) and the radius (r) by the angle variation (\Delta\theta),
| \Delta s=r \Delta\theta |
and then divide it by the time elapsed (\Delta t), we obtain the relationship that allows us to calculate the speed (v) along the orbit, known as the tangential velocity, which is associated with the angular Speed (\omega):
As the mean Speed (\bar{v}) is with the distance traveled in a time (\Delta s) and the time elapsed (\Delta t), equal to
| \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t } |
and with the distance traveled in a time (\Delta s) expressed as an arc of a circle, and the radius (r) and the angle variation (\Delta\theta) are
| \Delta s=r \Delta\theta |
and the definition of the mean angular velocity (\bar{\omega}) is
| \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t } |
then,
v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega
Since the relationship is general, it can be applied for instantaneous values, resulting in
| v = r \omega |
.
ID:(3233, 0)
Rotating body speed x
Equation 
Since the vortex rotates at the angular velocity of the object in the vortex (\omega) and is located ($$) from its center, the object moves at ($$):
| v_t = r \omega |
If a body is at ($$) and the velocity in the x direction is the speed x of the vortex center (U), then coordenada x de la velocidad del drifter (u) is:
ID:(11493, 0)
Rotating body speed y
Equation 
Given that the vortex rotates at the angular velocity of the object in the vortex (\omega) and is located ($$) from its center, the object moves at ($$):
| v_t = r \omega |
If a body is at ($$) and the velocity in the y direction is the speed y of the vortex center (V), then coordenada y de la velocidad del drifter (v) is:
ID:(11494, 0)
