Storyboard

Cada vez que se observa un objeto que se desplaza en línea recta a una velocidad constante desde un sistema en rotación (por ejemplo, la superficie de la Tierra), parece que realiza un movimiento curvo. Este fenómeno se puede modelar introduciendo una fuerza ficticia conocida como fuerza de Coriolis. Esta fuerza nos ayuda a comprender una serie de movimientos que se observan en los océanos y en la atmósfera.

>Modelo

ID:(1521, 0)

Iframe

>Top

ID:(15447, 0)

Video

>Top

En el video, se puede observar cómo un objeto parece seguir una trayectoria curva cuando se lo observa desde un sistema en rotación. Sin embargo, desde un sistema de referencia que no rota, su movimiento parece ser rectilíneo y con velocidad constante.

Para describir este fenómeno, se utiliza el concepto de la fuerza de Coriolis, que es una fuerza ficticia introducida para explicar el movimiento de un cuerpo en línea recta desde un sistema de referencia en rotación. Esta fuerza ficticia es fundamental para comprender una serie de fenómenos observados en océanos y atmósferas en movimiento.

ID:(11671, 0)

Concepto

>Top

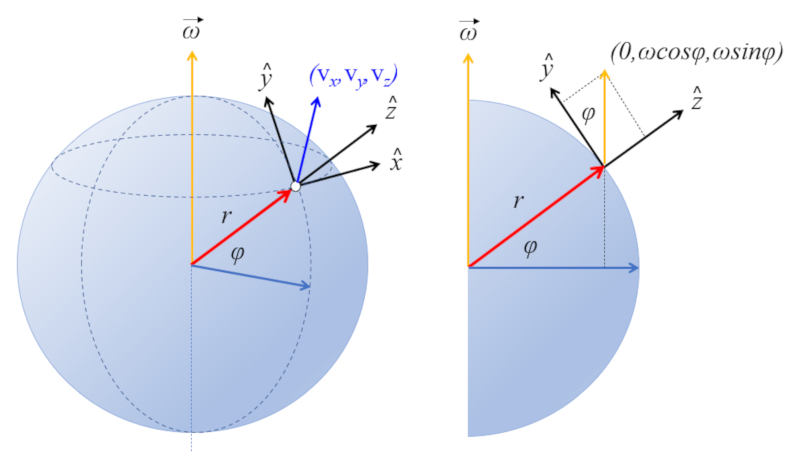
Se establece un sistema de referencia local en que se define:

• el eje z apunta hacia arriba
• el eje y apunta hacia el norte
• el eje x apunta hacia el este

Con ello el vector de la velocidad angular del planeta está en el plano yz con una angulo igual a la latitud del lugar:

ID:(11672, 0)

Concepto

>Top

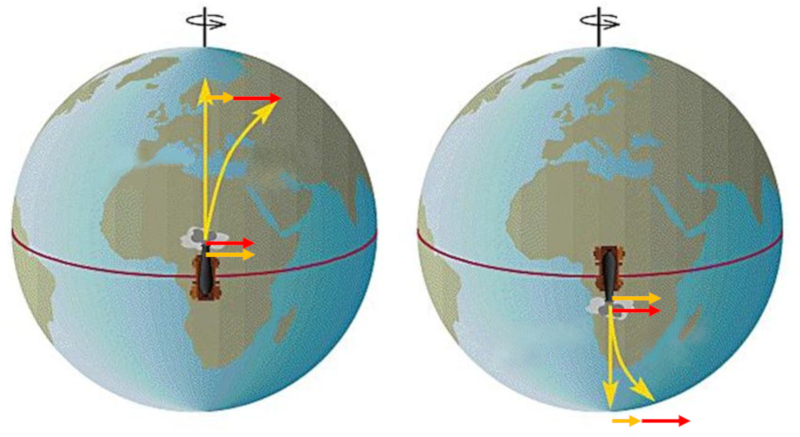
El efecto del aparente desvío se observa especialmente en la superficie terrestre. Si se lanza un objeto desde el ecuador hacia latitudes más altas, se nota que este "adelanta" su trayectoria debido a que, en latitudes más altas, la velocidad tangencial es menor que en el ecuador:

ID:(11673, 0)

Concepto

>Top

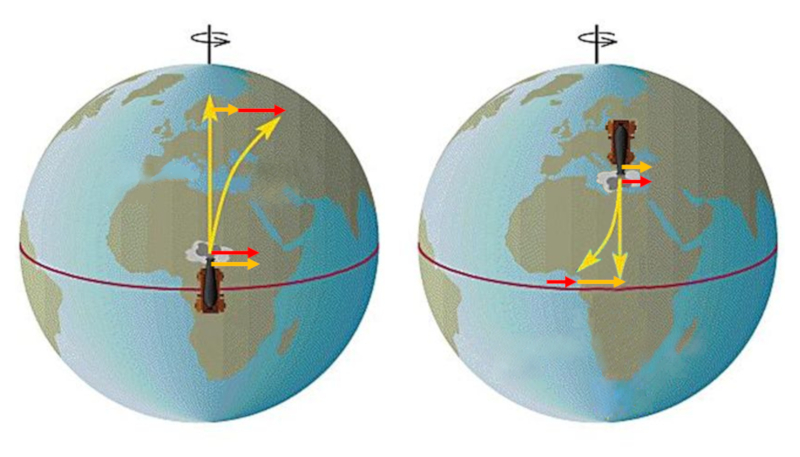
Si un objeto se lanza desde un lugar lejos del ecuador hacia el este, se observará que el cuerpo se desvía, retrocediendo, debido a su menor velocidad tangencial en comparación con las latitudes más cercanas al ecuador.

ID:(11674, 0)

Concepto

>Top

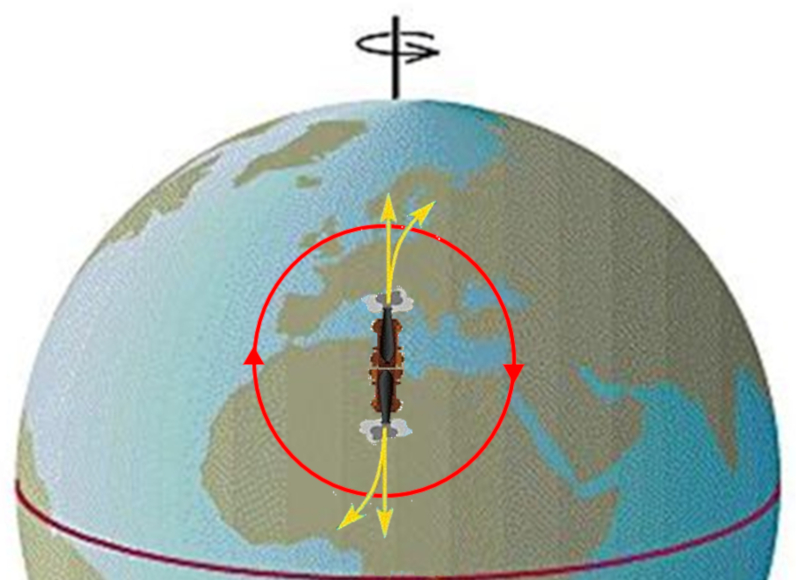
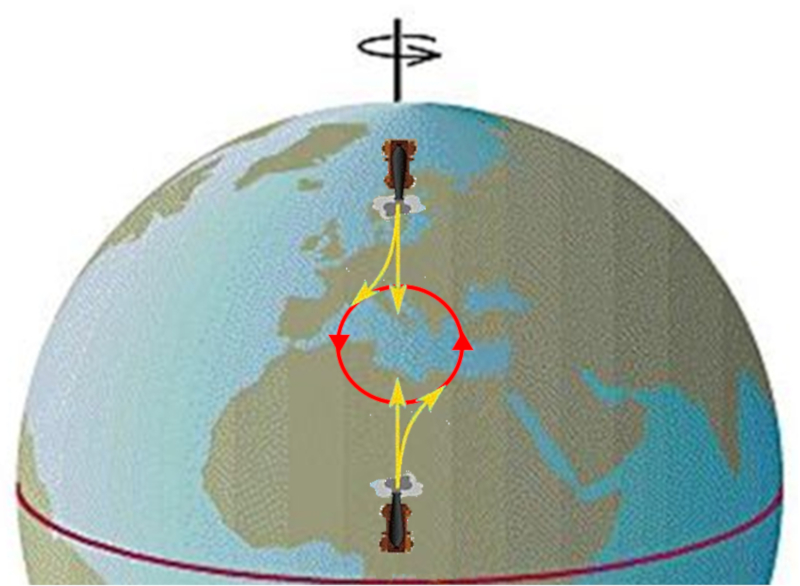
Si el medio que fluye se desplaza desde un punto, como por ejemplo una alta presión en el aire, los flujos se retrasan o adelantan según se dirijan hacia el ecuador o hacia el polo. Esto da lugar a la formación de un sistema que rota en sentido contrario a las agujas del reloj en el hemisferio norte, lo que se conoce como un ciclón.

ID:(11669, 0)

Concepto

>Top

Si el medio en movimiento fluye hacia un punto (por ejemplo, en el aire, desde una zona de baja presión), los flujos se adelantan o atrasan dependiendo de si vienen del ecuador o del polo. Esto resulta en la formación de un sistema que rota en sentido positivo (en el hemisferio norte), dando lugar a lo que se conoce como un anticiclón.

ID:(11675, 0)

Concepto

>Top

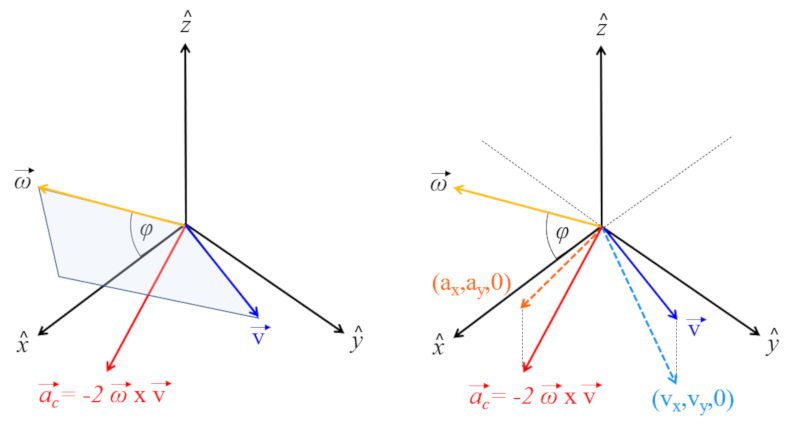
Si solo observamos lo que sucede en el plano, veremos que cada vez que nos desplazamos en una dirección particular, experimentamos una aceleración perpendicular en sentido positivo. La magnitud de esta aceleración aumenta con la latitud y es nula en el ecuador. Fuera de eso, es proporcional a la velocidad angular, lo que significa que si el sistema de referencia no girara, no existiría un efecto Coriolis.

ID:(11692, 0)

Top

>Top

Parámetros

$f$

f

Factor de Coriolis

rad/s

$\varphi$

phi

Latitud

rad

$\omega$

omega

Velocidad angular del planeta

rad/s

Variables

$\vec{a}_c$

&a_c

Aceleración de Coriolis

m/s^2

$a_{c,x}$

a_cx

Aceleración de Coriolis en dirección x

m/s^2

$a_{c,y}$

a_cy

Aceleración de Coriolis en dirección y

m/s^2

$a_{c,z}$

a_cz

Aceleración de Coriolis en dirección z

m/s^2

$a_{s,x}$

a_sx

Aceleración de Coriolis en la superficie, en dirección x

m/s^2

$a_{s,y}$

a_sy

Aceleración de Coriolis en la superficie, en dirección y

m/s^2

$a_{s,z}$

a_sz

Aceleración de Coriolis en la superficie, en dirección z

m/s^2

$e$

e

Segundo factor de Coriolis

rad/s

$\vec{\omega}$

&omega

Velocidad angular

rad/s

$\vec{v}$

&v

Velocidad del cuerpo

m/s

$v_x$

v_x

Velocidad x del objeto

m/s

$v_y$

v_y

Velocidad y del objeto

m/s

$v_z$

v_z

Velocidad z del objeto

m/s

Cálculos

• Método alternativo
• Método tradicional
• Estrategia
• 2D
• 3D

Ecuación

Número

Primero, seleccione la ecuación: a , luego, seleccione la variable: a

---

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Cálculos

Símbolo

Ecuación

Resuelto

Traducido

Variable Dado Calcule Objetivo : Ecuación A utilizar

Ecuaciones

ID:(15436, 0)

Ecuación

>Top, >Modelo

La aceleración de Coriolis explica cómo un objeto se desvía de su ruta debido a la rotación del sistema de referencia.

Es importante entender que la 'fuerza', 'aceleración' o 'efecto' de Coriolis es un 'truco' matemático para calcular cómo se comporta un cuerpo cuando se ve desde un sistema en rotación. La ecuación que mejor modela este efecto es la aceleración de Coriolis ($\vec{a}_c$) con la velocidad angular ($\vec{\omega}$) y la velocidad del cuerpo ($\vec{v}$):

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

Condiciones

Variables

$\vec{a}_c$

Aceleración de Coriolis

$m/s^2$

8763

$\vec{\omega}$

Velocidad angular

$rad/s$

9893

$\vec{v}$

Velocidad del cuerpo

$m/s$

8764

Relación

ID:(11693, 0)

Ecuación

>Top, >Modelo

La aceleración de Coriolis ($\vec{a}_c$) es con la velocidad angular ($\vec{\omega}$) y la velocidad del cuerpo ($\vec{v}$):

Entonces, con la aceleración de Coriolis en dirección x ($a_{c,x}$) junto a la velocidad angular del planeta ($\omega$), la velocidad y del objeto ($v_y$), la velocidad z del objeto ($v_z$) y la latitud ($\varphi$), la componente x es.

$ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$

Condiciones

Variables

$a_{c,x}$

Aceleración de Coriolis en dirección x

$m/s^2$

8597

$\phi$

Latitud

$rad$

8596

$\omega$

Velocidad angular del planeta

$rad/s$

8595

$v_y$

Velocidad y del objeto

$m/s$

8513

$v_z$

Velocidad z del objeto

$m/s$

8594

Relación

Desarrollo

En la superficie de la tierra, su eje apunta hacia el norte con un ángulo igual a la latitud ($\varphi$) respecto al plano. Por lo tanto, la velocidad angular ($\vec{\omega}$) es igual a:

$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$

Y dado que la velocidad del cuerpo ($\vec{v}$) es:

$\vec{v}=(v_x,v_y,v_z)$

la definición de la aceleración de Coriolis ($\vec{a}_c$):

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

resulta en la componente x igual a:

$ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$

ID:(11694, 0)

Ecuación

>Top, >Modelo

La aceleración de Coriolis ($\vec{a}_c$) está relacionado con la velocidad angular ($\vec{\omega}$) y la velocidad del cuerpo ($\vec{v}$):

Así, con la aceleración de Coriolis en dirección y ($a_{c,y}$) junto a la velocidad angular del planeta ($\omega$), la velocidad x del objeto ($v_x$) y la latitud ($\varphi$), la componente y es:

$ a_{c,y} = -2 \omega v_x \sin \varphi$

Condiciones

Variables

$a_{c,y}$

Aceleración de Coriolis en dirección y

$m/s^2$

8598

$\phi$

Latitud

$rad$

8596

$\omega$

Velocidad angular del planeta

$rad/s$

8595

$v_x$

Velocidad x del objeto

$m/s$

8512

Relación

Desarrollo

En la superficie de la tierra, su eje apunta hacia el norte con un ángulo igual a la latitud ($\varphi$) respecto al plano. Por lo tanto, la velocidad angular ($\vec{\omega}$) es igual a:

$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$

Y dado que la velocidad del cuerpo ($\vec{v}$) es:

$\vec{v}=(v_x,v_y,v_z)$

la definición de la aceleración de Coriolis ($\vec{a}_c$):

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

resulta en la componente y igual a:

$ a_{c,y} = -2 \omega v_x \sin \varphi$

ID:(11695, 0)

Ecuación

>Top, >Modelo

La aceleración de Coriolis ($\vec{a}_c$) está relacionado con la velocidad angular ($\vec{\omega}$) y la velocidad del cuerpo ($\vec{v}$):

Así, con la aceleración de Coriolis en dirección z ($a_{c,z}$) junto a la velocidad angular del planeta ($\omega$), la velocidad x del objeto ($v_x$) y la latitud ($\varphi$), la componente y es:

$ a_{c,z} = 2 \omega v_x \cos \varphi$

Condiciones

Variables

$a_{c,z}$

Aceleración de Coriolis en dirección z

$m/s^2$

8599

$\phi$

Latitud

$rad$

8596

$\omega$

Velocidad angular del planeta

$rad/s$

8595

$v_x$

Velocidad x del objeto

$m/s$

8512

Relación

Desarrollo

En la superficie de la tierra, su eje apunta hacia el norte con un ángulo igual a la latitud ($\varphi$) respecto al plano. Por lo tanto, la velocidad angular ($\vec{\omega}$) es igual a:

$\vec{\omega}=(0,\omega\cos\varphi,\omega\sin\varphi)$

Y dado que la velocidad del cuerpo ($\vec{v}$) es:

$\vec{v}=(v_x,v_y,v_z)$

la definición de la aceleración de Coriolis ($\vec{a}_c$):

$ \vec{a}_c =-2 \vec{\omega} \times \vec{v}$

resulta en la componente z igual a:

$ a_{c,z} = 2 \omega v_x \cos \varphi$

ID:(11696, 0)

Ecuación

>Top, >Modelo

Para simplificar las ecuaciones, trabajamos con un factor de Coriolis ($f$), que es una constante para el lugar físico, ya que incluye la velocidad angular del planeta ($\omega$) para la Tierra y la latitud ($\varphi$) para el lugar:

$ f = 2 \omega \sin \varphi $

Condiciones

Variables

$f$

Factor de Coriolis

$rad/s$

8600

$\phi$

Latitud

$rad$

8596

$\omega$

Velocidad angular del planeta

$rad/s$

8595

Relación

En el hemisferio sur, la latitud es negativa, y con ella 8600, lo que explica que los sistemas roten en dirección opuesta al hemisferio norte.

ID:(11697, 0)

Ecuación

>Top, >Modelo

Para simplificar las ecuaciones, trabajamos con un segundo factor de Coriolis ($e$), que es una constante para el lugar físico, ya que incluye la velocidad angular del planeta ($\omega$) para la Tierra y la latitud ($\varphi$) para el lugar:

$ e = 2 \omega \cos \varphi $

Condiciones

Variables

$\varphi$

Latitud

$rad$

8596

$e$

Segundo factor de Coriolis

$rad/s$

10273

$\omega$

Velocidad angular del planeta

$rad/s$

8595

Relación

ID:(15450, 0)

Ecuación

>Top, >Modelo

Como la aceleración de Coriolis en dirección x ($a_{c,x}$) puede reescribirse con el factor de Coriolis ($f$) y bajo la condición de que no hay movimiento vertical:

$v_z = 0$

Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección x ($a_{s,x}$) es:

$ a_{s,x} = f v_y $

Condiciones

Variables

$a_{s,x}$

Aceleración de Coriolis en la superficie, en dirección x

$m/s^2$

8601

$f$

Factor de Coriolis

$rad/s$

8600

$v_y$

Velocidad y del objeto

$m/s$

8513

Relación

Desarrollo

Como la aceleración de Coriolis en dirección x ($a_{c,x}$) se compone de la velocidad angular del planeta ($\omega$), la latitud ($\varphi$), la velocidad y del objeto ($v_y$) y la velocidad z del objeto ($v_z$):

$ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$

y la definición de el factor de Coriolis ($f$) es:

$ f = 2 \omega \sin \varphi $

además de la restricción de un movimiento en la superficie en la que:

$v_z = 0$

esto lleva a que la aceleración de Coriolis en dirección x ($a_{c,x}$) sea:

$ a_{s,x} = f v_y $

ID:(11698, 0)

Ecuación

>Top, >Modelo

Como la aceleración de Coriolis en dirección x ($a_{c,x}$) puede reescribirse con el factor de Coriolis ($f$) y bajo la condición de que no hay movimiento vertical:

$v_z = 0$

Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección y ($a_{s,y}$) es:

$ a_{s,y} = - f v_x $

Condiciones

Variables

$a_{s,y}$

Aceleración de Coriolis en la superficie, en dirección y

$m/s^2$

8602

$f$

Factor de Coriolis

$rad/s$

8600

$v_x$

Velocidad x del objeto

$m/s$

8512

Relación

Desarrollo

Como la aceleración de Coriolis en dirección y ($a_{c,y}$) se compone de la velocidad angular del planeta ($\omega$), la velocidad x del objeto ($v_x$) y la latitud ($\varphi$):

$ a_{c,y} = -2 \omega v_x \sin \varphi$

y la definición de el factor de Coriolis ($f$) es:

$ f = 2 \omega \sin \varphi $

además de la restricción de un movimiento en la superficie en la que:

$v_z = 0$

esto lleva a que la aceleración de Coriolis en dirección y ($a_{c,y}$) sea:

$ a_{s,y} = - f v_x $

ID:(11699, 0)

Ecuación

>Top, >Modelo

Como la aceleración de Coriolis en dirección z ($a_{c,z}$) puede reescribirse con el segundo factor de Coriolis ($e$) y bajo la condición de que no hay movimiento vertical:

$v_z = 0$

Entonces, se deduce que la aceleración de Coriolis en la superficie, en dirección z ($a_{s,z}$) es:

$ a_{s,z} = e v_x $

Condiciones

Variables

$a_{s,z}$

Aceleración de Coriolis en la superficie, en dirección z

$m/s^2$

10274

$e$

Segundo factor de Coriolis

$rad/s$

10273

$v_x$

Velocidad x del objeto

$m/s$

8512

Relación

Desarrollo

Como la aceleración de Coriolis en dirección z ($a_{c,z}$) se compone de la velocidad angular del planeta ($\omega$), la velocidad x del objeto ($v_x$) y la latitud ($\varphi$):

$ a_{c,z} = 2 \omega v_x \cos \varphi$

y la definición de el segundo factor de Coriolis ($e$) es:

$ e = 2 \omega \cos \varphi $

además de la restricción de un movimiento en la superficie en la que:

$v_z = 0$

esto lleva a que la aceleración de Coriolis en la superficie, en dirección z ($a_{s,z}$) sea:

$ a_{s,z} = e v_x $

ID:(15451, 0)