Utilizador:
Movimento Oceânico, drifters
Storyboard 
O movimento na superfície dos oceanos surge da interação com a atmosfera e é condicionado às correntes mais profundas (com mais de 15 metros). Em uma primeira abordagem, pode ser considerado como um fluxo a uma velocidade constante com vórtices estáveis ou arrastados por ele.
ID:(1519, 0)
Mecanismos
Iframe
Mecanismos
ID:(15449, 0)
Rotação como translação, posição
Conceito
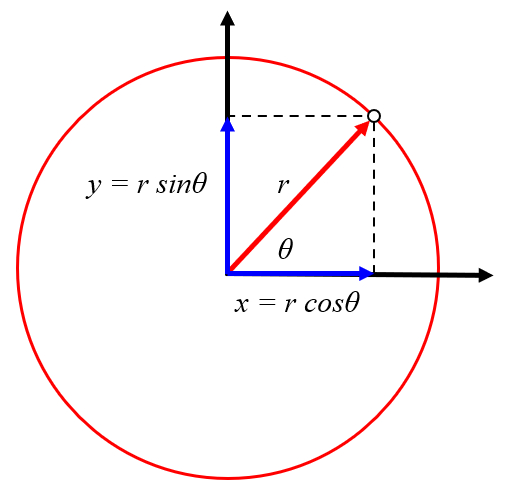
O movimento de rotação pode ser expresso como deslocamento nas direções x e y com valores de la distância do objeto ao centro do vórtice ($r$)8519 e o ângulo do objeto no vórtice ($\theta_w$)8516, respectivamente. Com as coordenadas la posição x do centro do vórtice ($X$)8506 e la posição y do centro do vórtice ($Y$)8507, obtemos que la posição x do objeto ($x$)8508 é:
| $ x = X + r \cos \theta_w$ |
e para la posição y do objeto ($y$)8509:
| $ y = Y + r \sin \theta_w$ |
ID:(11490, 0)
Rotação como translação, velocidade
Imagem
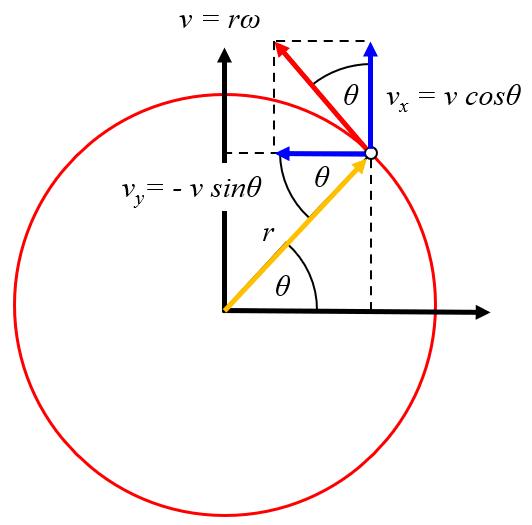
O movimento de rotação pode ser expresso como deslocamento nas direções x e y, com velocidades de ($$)9913 e ($$)9914, respectivamente. Com as coordenadas la velocidade x do centro do vórtice ($U$)8510 e la velocidade y do centro do vórtice ($V$)8511, obtemos que ($$)9913 é:
| $ u = U - r \omega \sin \theta_w $ |
| $ v = V + r \omega \cos \theta_w $ |
ID:(11489, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ r ^2=( X - x )^2 + ( Y - y )^2 $
r ^2=( X - x )^2 + ( Y - y )^2
$ \theta_w = \theta_0 + \omega t $
theta_w = theta_0 + omega * t
$ u = U - r \omega \sin \theta_w $
u = U - r * omega * sin( theta_w )
$ v_t = r \omega $
v = r * omega
$ v = V + r \omega \cos \theta_w $
v = V + r * omega * cos( theta_w )
$ x = X + r \cos \theta_w$
x = X + r * cos( theta_w )
$ X = X_0 + U t $
X = X_0 + U * t
$ y = Y + r \sin \theta_w$
y = Y + r * sin( theta_w )
$ Y = Y_0 + V t $
Y = Y_0 + V * t
ID:(15445, 0)
Posição do vértice x
Equação
O vórtice se move na direção $x$ com uma constante de uma velocidade x do centro do vórtice ($U$)8510,1, partindo de uma posição inicial x ($X_0$)8514,1 e alcançando em o tempo desde o início do rastreamento ($t$)8520 em $x$ La posição x do centro do vórtice ($X$)8506:
| $ X = X_0 + U t $ |
ID:(11495, 0)
Posição do vértice y
Equação
O vórtice se move na direção $y$ com uma constante de uma velocidade y do centro do vórtice ($V$)8511,1, partindo de uma posição inicial y ($Y_0$)8515,1 e alcançando em o tempo desde o início do rastreamento ($t$)8520 em $y$ La posição y do centro do vórtice ($Y$)8507:
| $ Y = Y_0 + V t $ |
ID:(11496, 0)
Ângulo $\theta$ do vórtice
Equação
O vórtice gira constantemente em ($$)8518,1, partindo de um ângulo inicial do objeto no vórtice ($\theta_0$)8517,1 e chegando em o tempo desde o início do rastreamento ($t$)8520 a um ângulo do objeto no vórtice ($\theta_w$)8516,1:
| $ \theta_w = \theta_0 + \omega t $ |
ID:(11497, 0)
Distância do objeto ao centro do vórtice
Equação
A distância entre o objeto em la posição x do objeto ($x$)8508 e la posição y do objeto ($y$)8509 e o centro dos vórtices em la posição x do centro do vórtice ($X$)8506 e la posição y do centro do vórtice ($Y$)8507 pode ser calculada usando o teorema de Pitágoras, resultando em la distância do objeto ao centro do vórtice ($r$)8519:
| $ r ^2=( X - x )^2 + ( Y - y )^2 $ |
ID:(11500, 0)
Posição x do corpo em rotação
Equação
Se um corpo gira a um ângulo de o ângulo do objeto no vórtice ($\theta_w$)8516 a uma distância de la distância do objeto ao centro do vórtice ($r$)8519 de um centro localizado na posição la posição x do centro do vórtice ($X$)8506, o resultado é Uma posição x do objeto ($x$)8508,1:
| $ x = X + r \cos \theta_w$ |
ID:(11491, 0)
Posição y do corpo em rotação
Equação
Se um corpo gira a um ângulo de o ângulo do objeto no vórtice ($\theta_w$)8516 a uma distância de la distância do objeto ao centro do vórtice ($r$)8519 de um centro localizado na posição la posição y do centro do vórtice ($Y$)8507, o resultado será Uma posição y do objeto ($y$)8509,1:
| $ y = Y + r \sin \theta_w$ |
ID:(11492, 0)
Velocidade e velocidade angular
Equação
Se dividirmos a relação entre la distância percorrida em um tempo ($\Delta s$)6025 e o rádio ($r$)9894 por la variação de ângulo ($\Delta\theta$)6066,
| $ \Delta s=r \Delta\theta $ |
e então dividirmos isso por o tempo decorrido ($\Delta t$)5103, obtemos a relação que nos permite calcular la velocidade ($v$)6029 ao longo da órbita, conhecida como velocidade tangencial, que está associada a la velocidade angular ($\omega$)6068:
| $ v_t = r \omega $ |
| $ v = r \omega $ |
Como la velocidade média ($\bar{v}$)5268 é com la distância percorrida em um tempo ($\Delta s$)6025 e o tempo decorrido ($\Delta t$)5103, igual a
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
e com la distância percorrida em um tempo ($\Delta s$)6025 expresso como arco de um círculo, e o rádio ($r$)9894 e la variação de ângulo ($\Delta\theta$)6066 são
| $ \Delta s=r \Delta\theta $ |
e a definição de la velocidade angular média ($\bar{\omega}$)9943 é
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
então,
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Como a relação é geral, pode ser aplicada para valores instantâneos, resultando em
| $ v = r \omega $ |
ID:(3233, 0)
Velocidade x do corpo em rotação
Equação
Uma vez que o vórtice rotaciona a ($$)8518 e está localizado a uma distância do objeto ao centro do vórtice ($r$)8519,1 do seu centro, o objeto se move a uma velocidade tangencial do drifter ($v_t$)10336,1:
Se um corpo está em um ângulo do objeto no vórtice ($\theta_w$)8516,1 e a velocidade na direção $x$ é La velocidade x do centro do vórtice ($U$)8510, então ($$)9913 é:
| $ u = U - r \omega \sin \theta_w $ |
ID:(11493, 0)
Velocidade y do corpo em rotação
Equação
Dado que o vórtice gira a ($$)8518 e está localizado a uma distância do objeto ao centro do vórtice ($r$)8519,1 do seu centro, o objeto se desloca a uma velocidade tangencial do drifter ($v_t$)10336,1:
Se um corpo está em um ângulo do objeto no vórtice ($\theta_w$)8516,1 e a velocidade na direção $y$ é La velocidade y do centro do vórtice ($V$)8511, então ($$)9914 é:
| $ v = V + r \omega \cos \theta_w $ |
ID:(11494, 0)