Benützer:
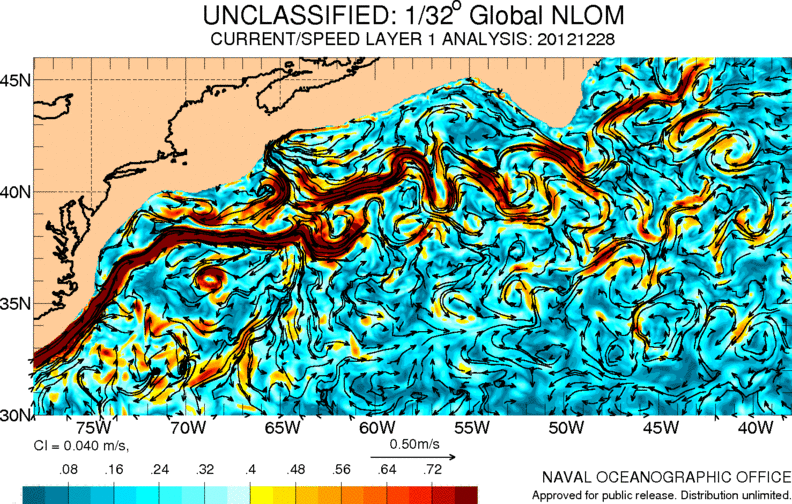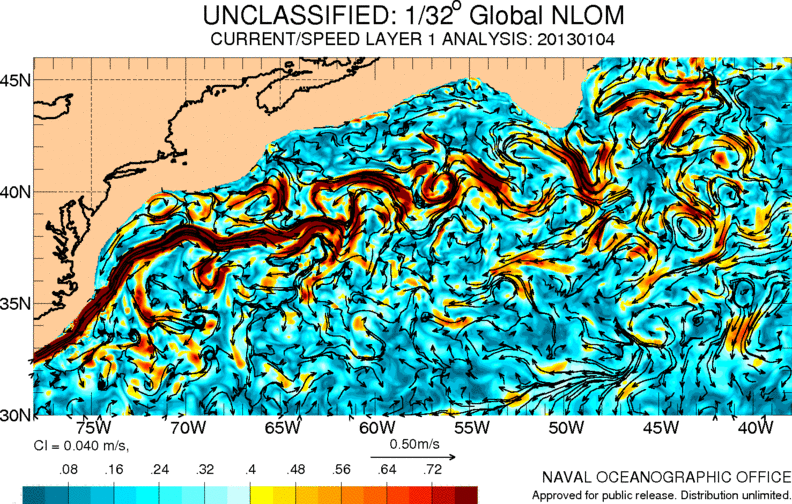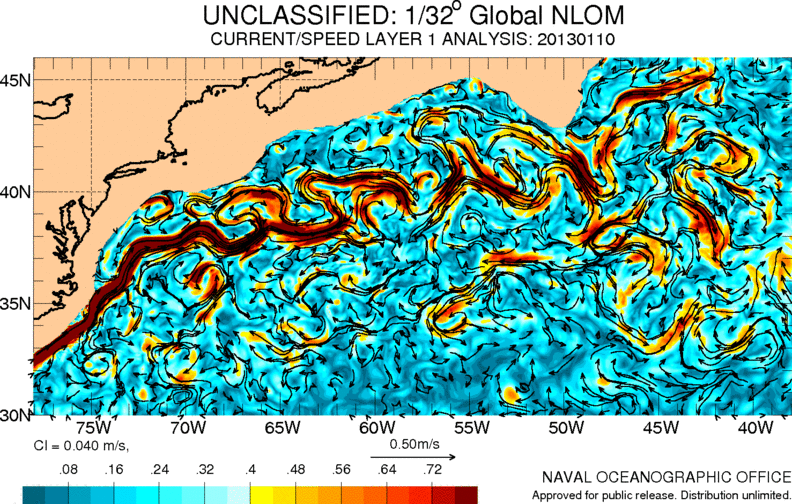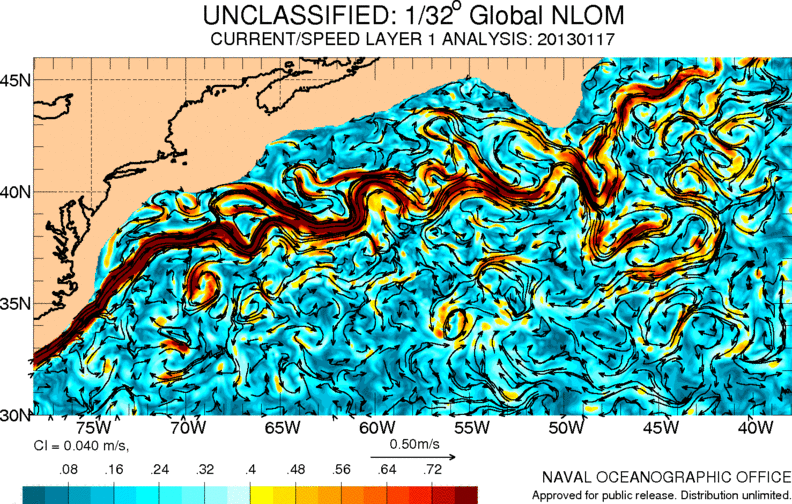
Ozeanbewegung, Drifters
Storyboard 
Die Bewegung an der Oberfläche der Ozeane entsteht durch die Wechselwirkung mit der Atmosphäre und wird durch die tieferen Strömungen (mehr als 15 Meter) bedingt. In einer ersten Annäherung kann sie als ein Fluss mit konstanter Geschwindigkeit mit stabilen Wirbeln oder solchen, die von ihm mitgezogen werden, betrachtet werden.
ID:(1519, 0)
Mechanismen
Iframe
Mechanismen
ID:(15449, 0)
Ozeanbewegungen
Video
Die Bewegung des Ozeans wird an der Oberfläche durch die Bewegung der Luft in der Tiefe durch Schwankungen der Dichte erzeugt, die durch Temperatur und Salzgehalt bedingt sind. Im folgenden NASA-Video werden verschiedene Effekte gezeigt:
ID:(11485, 0)
Strömungen in Mittelamerika und der Karibik
Bild
Der Golfstrom stammt aus der Karibik, wo es auch eine Reihe von Zirkulationen gibt, die mit den Bewegungen der Luftmassen in der Region verbunden sind:
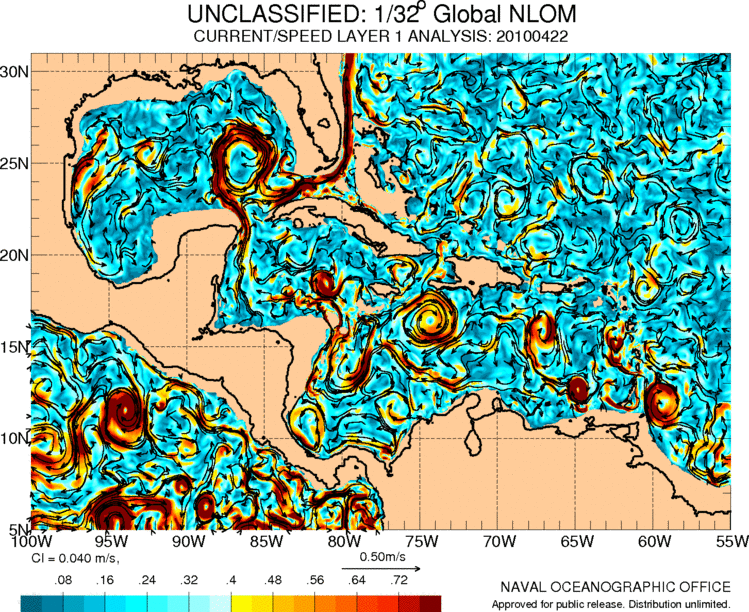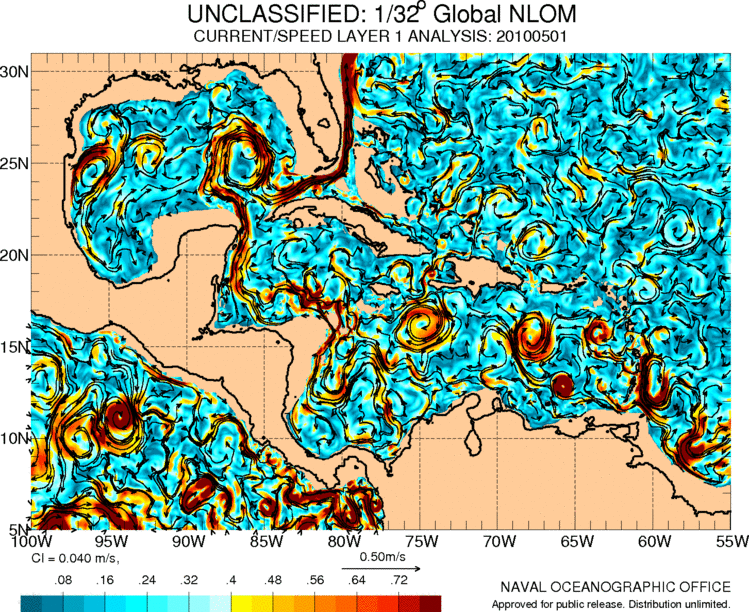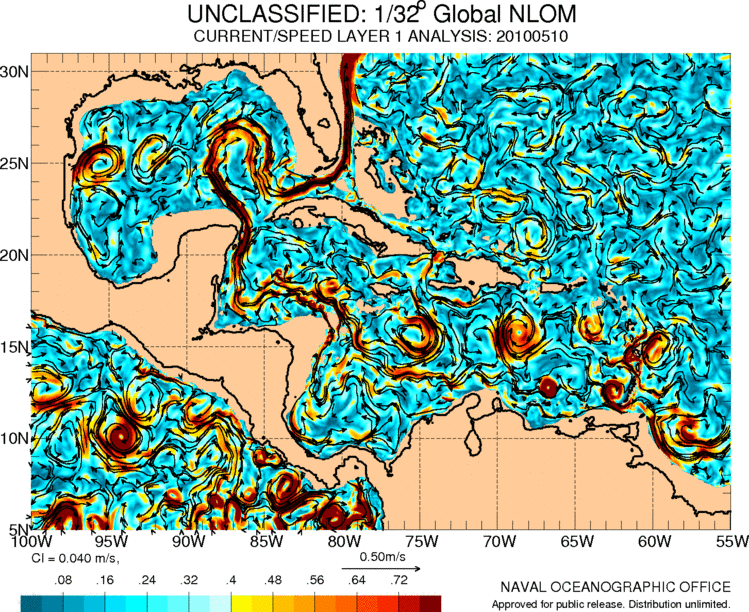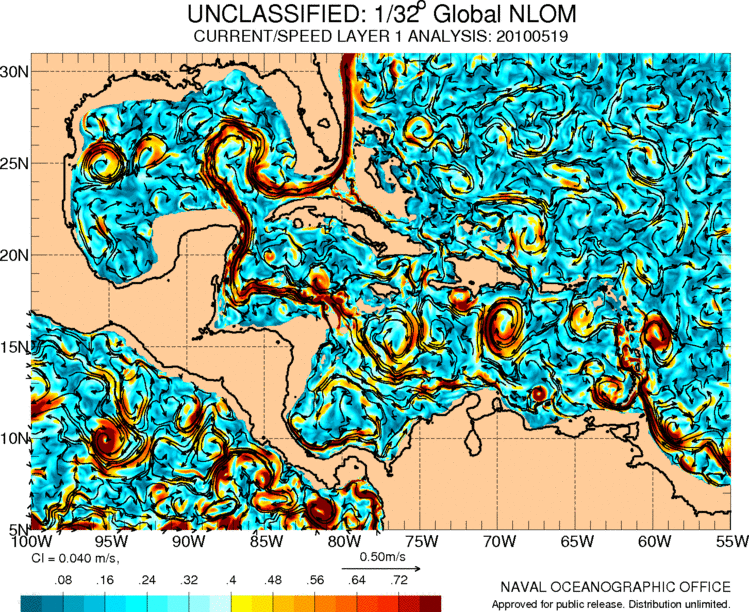
ID:(11487, 0)
X-15 Ben Franklin Bewegung
Bild
1969 wurde das Tauchboot X-15 Ben Franklin des Entdeckers Jacques Piccard vom Golfstrom mitgerissen. Ich schwebe dafür in einer Tiefe, die einer neutralen Flotation (zwischen 180 und 610 m) entspricht und 2324 km zurücklegt:
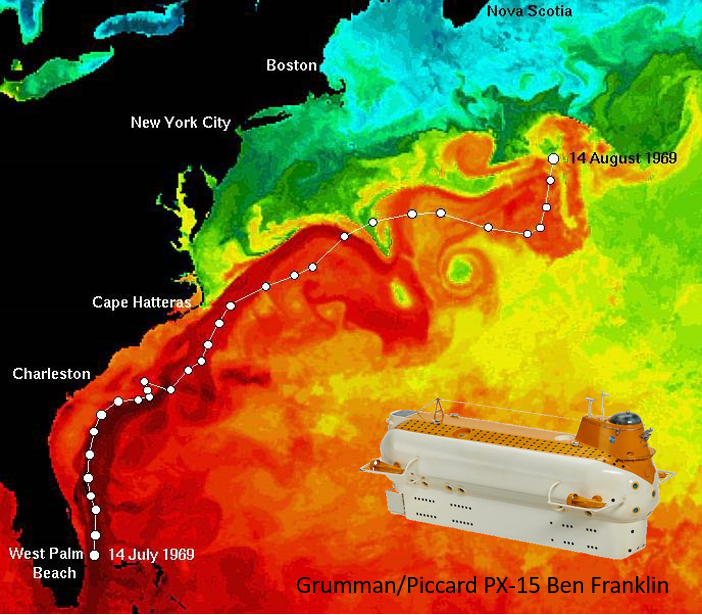
ID:(11488, 0)
Drifter (freie Boje)
Konzept
Um die Meeresströmungen in der oberen Schicht durch Messen der Position (und damit der Geschwindigkeit), der Strahlung, der Temperatur und des Salzgehalts zu untersuchen, werden freie Bojen verwendet, die als langrangische Drifter oder Drifter bezeichnet werden:
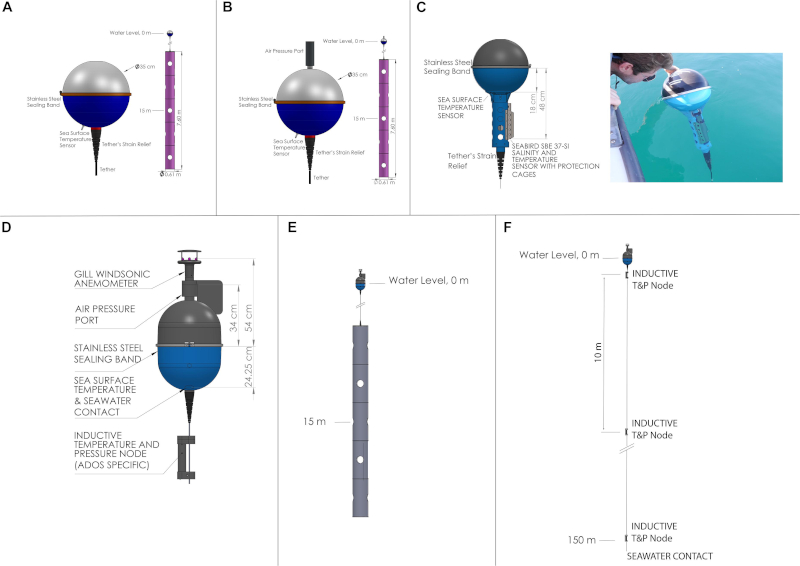
ID:(11498, 0)
Drifterverteilung (freie Boje)
Konzept
Es gibt verschiedene Programme, die Drifers über alle Ozeane verteilt haben, um den Fluss im Ozean zu überwachen. Ein Beispiel ist das Global Drifter Program (GDP), das die folgende Verteilung aufweist:
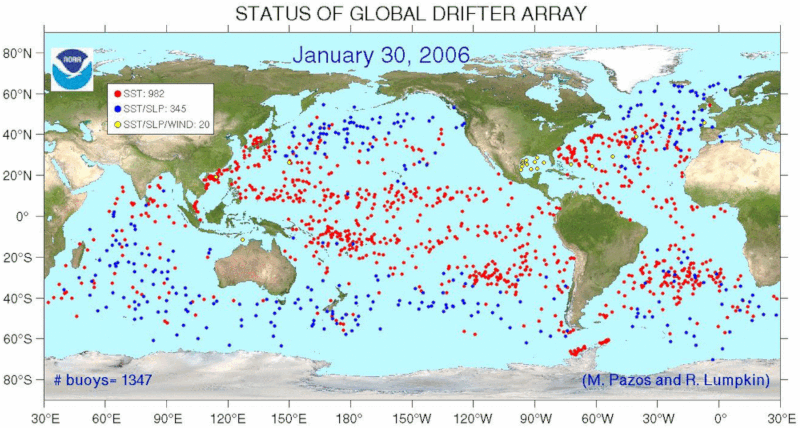
ID:(11499, 0)
Rotation als Traslation, Position
Konzept
Die Rotationsbewegung kann als Verschiebung in den x- und y-Richtungen mit den Werten von die Objektabstand vom Wirbelzentrum ($r$)8519 und der Objektwinkel im Wirbel ($\theta_w$)8516 ausgedrückt werden. Mit den Koordinaten die Position x des Wirbelzentrums ($X$)8506 und die Position y des Wirbelzentrums ($Y$)8507 erhalten wir, dass die Position x des Objekt ($x$)8508 ist:
| $ x = X + r \cos \theta_w$ |
und für die Position y des Objekt ($y$)8509:
| $ y = Y + r \sin \theta_w$ |
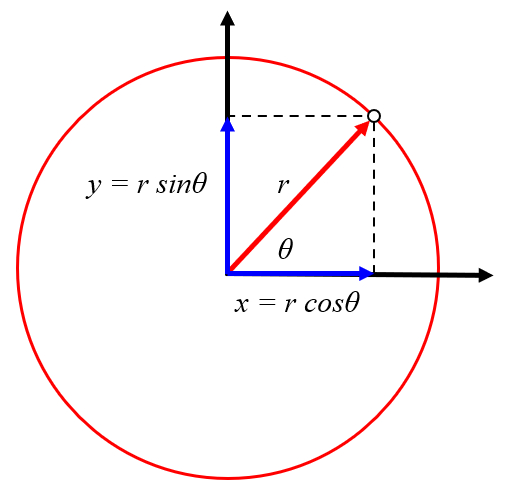
ID:(11490, 0)
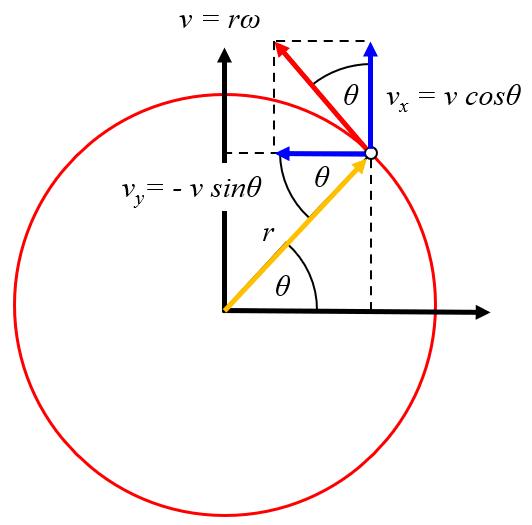
Rotation als Traslation, Geschwindigkeit
Bild
Die Rotationsbewegung kann als Verschiebung in den Richtungen x und y mit Geschwindigkeiten von Coordenada x de la velocidad del drifter ($u$)9913 und Coordenada y de la velocidad del drifter ($v$)9914 ausgedrückt werden. Mit den Koordinaten die Geschwindigkeit x des Wirbelzentrums ($U$)8510 und die Geschwindigkeit y des Wirbelzentrums ($V$)8511 erhalten wir, dass Coordenada x de la velocidad del drifter ($u$)9913 ist:
| $ u = U - r \omega \sin \theta_w $ |
und für Coordenada y de la velocidad del drifter ($v$)9914:
| $ v = V + r \omega \cos \theta_w $ |
ID:(11489, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ r ^2=( X - x )^2 + ( Y - y )^2 $
r ^2=( X - x )^2 + ( Y - y )^2
$ \theta_w = \theta_0 + \omega t $
theta_w = theta_0 + omega * t
$ u = U - r \omega \sin \theta_w $
u = U - r * omega * sin( theta_w )
$ v_t = r \omega $
v = r * omega
$ v = V + r \omega \cos \theta_w $
v = V + r * omega * cos( theta_w )
$ x = X + r \cos \theta_w$
x = X + r * cos( theta_w )
$ X = X_0 + U t $
X = X_0 + U * t
$ y = Y + r \sin \theta_w$
y = Y + r * sin( theta_w )
$ Y = Y_0 + V t $
Y = Y_0 + V * t
ID:(15445, 0)
Position x des Wirbels
Gleichung
Der Wirbel bewegt sich in Richtung $x$ mit einer Konstanten von eine Geschwindigkeit x des Wirbelzentrums ($U$)8510,1, von eine Ausgangsposition x ($X_0$)8514,1 aus und erreicht bei der Zeit vom Beginn der Ablaufverfolgung ($t$)8520 in $x$ Die Position x des Wirbelzentrums ($X$)8506:
| $ X = X_0 + U t $ |
ID:(11495, 0)
Position y des Wirbels
Gleichung
Der Wirbel bewegt sich in Richtung $y$ mit einer Konstanten von eine Geschwindigkeit y des Wirbelzentrums ($V$)8511,1, von eine Ausgangsposition y ($Y_0$)8515,1 aus und erreicht bei der Zeit vom Beginn der Ablaufverfolgung ($t$)8520 in $y$ Die Position y des Wirbelzentrums ($Y$)8507:
| $ Y = Y_0 + V t $ |
ID:(11496, 0)
Winkel $\theta$ des Wirbels
Gleichung
Der Wirbel rotiert gleichmäßig mit einer Konstanten von eine Winkelgeschwindigkeit des Objekt im Wirbel ($\omega$)8518,1, beginnend bei ein Anfangswinkel des Objekt im Wirbel ($\theta_0$)8517,1 und erreicht bei der Zeit vom Beginn der Ablaufverfolgung ($t$)8520 Ein Objektwinkel im Wirbel ($\theta_w$)8516,1:
| $ \theta_w = \theta_0 + \omega t $ |
ID:(11497, 0)
Abstand des Objekts zur Mitte des Wirbels
Gleichung
Die Entfernung zwischen dem Objekt in die Position x des Objekt ($x$)8508 und die Position y des Objekt ($y$)8509 und dem Zentrum des Wirbels in die Position x des Wirbelzentrums ($X$)8506 und die Position y des Wirbelzentrums ($Y$)8507 kann mit dem Satz des Pythagoras berechnet werden, was zu die Objektabstand vom Wirbelzentrum ($r$)8519 führt:
| $ r ^2=( X - x )^2 + ( Y - y )^2 $ |
ID:(11500, 0)
Position x des rotierenden Körpers
Gleichung
Wenn ein Körper sich um einen Winkel von der Objektwinkel im Wirbel ($\theta_w$)8516 bei einer Entfernung von die Objektabstand vom Wirbelzentrum ($r$)8519 von einem Zentrum, das sich an der Position die Position x des Wirbelzentrums ($X$)8506 befindet, dreht, ergibt sich eine Position x des Objekt ($x$)8508,1:
| $ x = X + r \cos \theta_w$ |
ID:(11491, 0)
Position y des rotierenden Körpers
Gleichung
Wenn ein Körper sich um einen Winkel von der Objektwinkel im Wirbel ($\theta_w$)8516 bei einer Entfernung von die Objektabstand vom Wirbelzentrum ($r$)8519 von einem Zentrum, das sich an der Position die Position y des Wirbelzentrums ($Y$)8507 befindet, dreht, ergibt sich eine Position y des Objekt ($y$)8509,1:
| $ y = Y + r \sin \theta_w$ |
ID:(11492, 0)
Geschwindigkeit und Winkelgeschwindigkeit
Gleichung
Wenn wir das Verhältnis zwischen die Zurückgelegte Strecke in einer Zeit ($\Delta s$)6025 und der Radius ($r$)9894 durch die Winkelvariation ($\Delta\theta$)6066 teilen,
| $ \Delta s=r \Delta\theta $ |
und das dann durch der Abgelaufene Zeit ($\Delta t$)5103 teilen, erhalten wir die Beziehung, die es uns ermöglicht, die Geschwindigkeit ($v$)6029 entlang der Umlaufbahn zu berechnen, bekannt als die tangentielle Geschwindigkeit, die mit die Winkelgeschwindigkeit ($\omega$)6068 verbunden ist:
| $ v_t = r \omega $ |
| $ v = r \omega $ |
Da die Mittlere Geschwindigkeit ($\bar{v}$)5268 mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$)6025 und der Abgelaufene Zeit ($\Delta t$)5103 gleich ist, was ist
| $ \bar{v} \equiv\displaystyle\frac{ \Delta s }{ \Delta t }$ |
und mit die Zurückgelegte Strecke in einer Zeit ($\Delta s$)6025 als Bogen eines Kreises und der Radius ($r$)9894 und die Winkelvariation ($\Delta\theta$)6066 ist
| $ \Delta s=r \Delta\theta $ |
und die Definition von die Mittlere Winkelgeschwindigkeit ($\bar{\omega}$)9943 ist
| $ \bar{\omega} \equiv\displaystyle\frac{ \Delta\theta }{ \Delta t }$ |
dann ist
$v=\displaystyle\frac{\Delta s}{\Delta t}=r\displaystyle\frac{\Delta\theta}{\Delta t}=r\omega$
Da die Beziehung allgemein ist, kann sie für momentane Werte angewendet werden, was zu
| $ v = r \omega $ |
führt.
ID:(3233, 0)
Geschwindigkeit x des rotierenden Körpers
Gleichung
Da sich der Wirbel mit die Winkelgeschwindigkeit des Objekt im Wirbel ($\omega$)8518 Umdrehungen pro Minute dreht und sich eine Objektabstand vom Wirbelzentrum ($r$)8519,1 von seinem Zentrum befindet, bewegt sich das Objekt mit eine Tangentialgeschwindigkeit des Drifters ($v_t$)10336,1:
| $ v_t = r \omega $ |
Wenn sich ein Körper bei ein Objektwinkel im Wirbel ($\theta_w$)8516,1 befindet und die Geschwindigkeit in Richtung $x$ Die Geschwindigkeit x des Wirbelzentrums ($U$)8510 beträgt, dann beträgt Coordenada x de la velocidad del drifter ($u$)9913:
| $ u = U - r \omega \sin \theta_w $ |
ID:(11493, 0)
Geschwindigkeit y des rotierenden Körpers
Gleichung
Angesichts der Tatsache, dass sich der Wirbel mit die Winkelgeschwindigkeit des Objekt im Wirbel ($\omega$)8518 Umdrehungen pro Minute dreht und eine Objektabstand vom Wirbelzentrum ($r$)8519,1 von seinem Zentrum entfernt ist, bewegt sich das Objekt mit eine Tangentialgeschwindigkeit des Drifters ($v_t$)10336,1:
| $ v_t = r \omega $ |
Wenn sich ein Körper bei ein Objektwinkel im Wirbel ($\theta_w$)8516,1 befindet und die Geschwindigkeit in Richtung $y$ Die Geschwindigkeit y des Wirbelzentrums ($V$)8511 beträgt, dann beträgt Coordenada y de la velocidad del drifter ($v$)9914:
| $ v = V + r \omega \cos \theta_w $ |
ID:(11494, 0)