Benützer: 
Bewegung an den Küstenrändern
Storyboard 
An der Küste kann die Coriolis-Kraft zu einer Zirkulation führen, die nährstoffreiches Material an die Oberfläche zieht (Ekman-Transport).
ID:(1578, 0)
Ekman Transport
Konzept
Cuando existen corrientes en dirección del ecuador en los lados oeste en bordes continentales, la ecuación de Coriolis para el plano con
| $ a_{s,y} = - f v_x $ |
implica que existe una corriente que se aleja de la costa. Esto genera una corriente que lleva aguas frías ricas en nutrientes a la superficie:
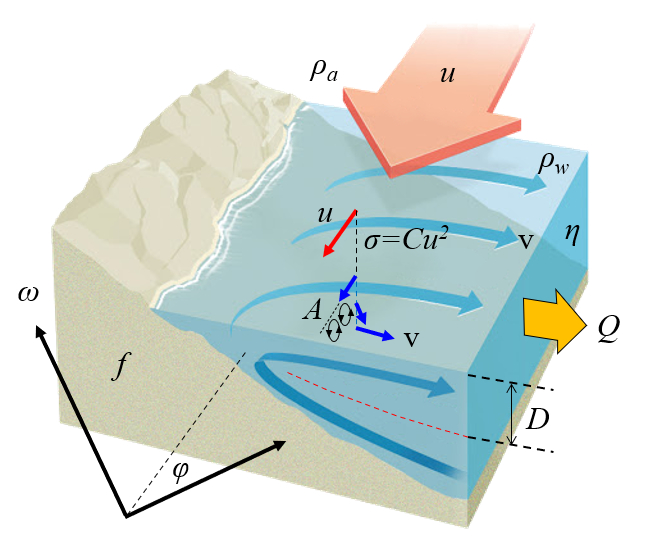
Este transporte se denomina el transporte de Ekman.
ID:(11679, 0)
Charakterisierung der Ozeanschichten
Bild
Durch Ekmans Transport verschieben sich die Grenzen zwischen den Oberflächenschichten und den tiefsten Schichten im Ozean. Diese sind durch plötzliche Änderungen der Parameter in Abhängigkeit von der Temperatur gekennzeichnet. Insbesondere gibt es Änderungen in:
• Temperatur (Thermokline)
• Salzgehalt (Halokline)
• Dichte (Pyknokline)
ID:(11684, 0)
Invers Ekman Transport
Bild
Si se invierte el sentido del viento para el transporte de Ekman se tiene el proceso inverso (si
En este caso se tiene que con la velocidad hacia los polos resulta
| $ a_{s,y} = - f v_x $ |
Esto implica que existe una corriente que va hacia la costa evitando que los nutrientes lleguen a la superficie:
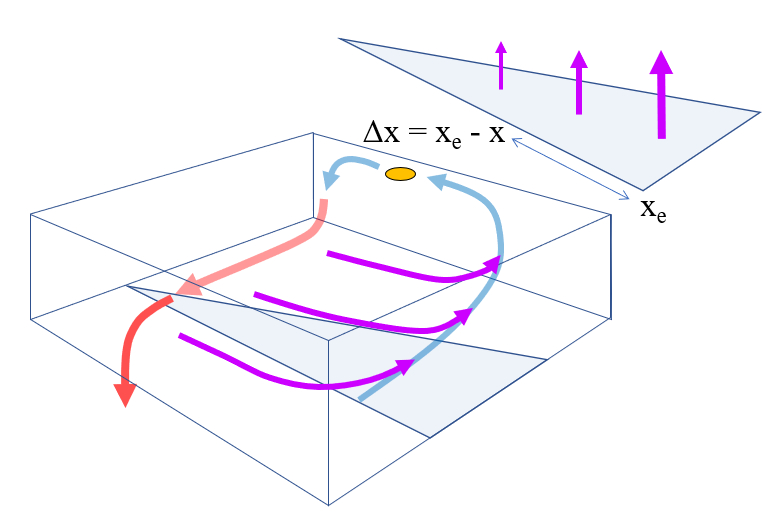
ID:(11680, 0)
Aufwärtszonen (upwelling)
Bild
Existen distintas zonas en el mundo en donde por vientos, ya sea en forma permanente o estacional, existe surgencia. Esto lleva a que en estos lugares las corrientes que van en dirección de la costa arrastran aguas frias ricas en vida en dirección de la superficie con lo que se favorece la vida en la superficie.
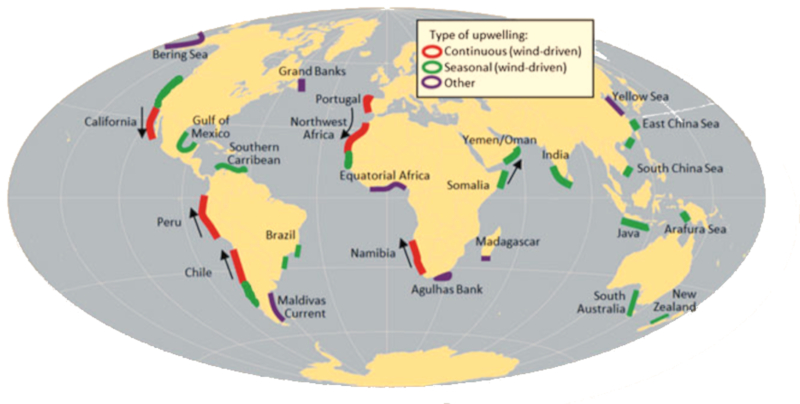
ID:(11700, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ D_E =\sqrt{\displaystyle\frac{2 \pi A_z }{ f }}$
D_E =sqrt( 2 * pi * A_z / f )
$ Q = D_E u_e $
Q = D_E * u_e
$ \tau_w = \rho_a C_D U ^2$
tau_w = rho_a * C_D * U ^2
$ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$
u_e = tau_w /( f * rho_w * D_E )
ID:(15443, 0)
Vom Wind erzeugte Oberflächenspannung
Gleichung
Die Energiedichte des Windes ist eine Funktion von die Luftdichte ($\rho_a$) und die Windgeschwindigkeit ($U$) in der Form
$\displaystyle\frac{1}{2}\rho_aU^2$
Wenn nur ein Teil der Energie übertragen wird, kann die Vom Wind erzeugte Spannung ($\tau_w$) als die Energiedichte multipliziert mit einem Faktor die Widerstandsbeiwert ($C_D$) modelliert werden:
| $ \tau_w = \rho_a C_D U ^2$ |
ID:(11718, 0)
Ekmans Tiefe
Gleichung
Die Spannung an der Meeresoberfläche, die durch den Wind erzeugt wird, wird durch Wirbel in die Tiefe übertragen, was dazu führt, dass die Wassermasse mitgezogen wird. Die Tiefe des Wassers, oder die Ekmans Tiefe ($D_E$), das mitgezogen werden kann, hängt davon ab, wie die Energie in tiefere Schichten diffundiert, was die Wirbelviskosität zum vertikalen Mischen ($A_z$) entspricht. Es ist, mit der Coriolis-Faktor ($f$), gleich:
| $ D_E =\sqrt{\displaystyle\frac{2 \pi A_z }{ f }}$ |
ID:(11670, 0)
Ekman Strömungsgeschwindigkeit
Gleichung
Die durch den Wind erzeugte die Vom Wind erzeugte Spannung ($\tau_w$) führt zur Oberflächengeschwindigkeit des Ozeans oder die Ekmans Geschwindigkeit ($u_e$), die wiederum durch die Corioliskraft, dargestellt durch der Coriolis-Faktor ($f$), den Ekman-Transport erzeugt. Dies geschieht mit die Dichte des Meerwassers ($\rho$) und die Ekmans Tiefe ($D_E$):
| $ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$ |
Mit die Vom Wind erzeugte Spannung ($\tau_w$) über der Oberfläche $S$ des Ozeans entsteht eine Kraft:
$F = \sigma_w S$
die auf die Masse $m$ wirkt, die aus die Dichte des Meerwassers ($\rho$), die Ekmans Tiefe ($D_E$) und der Oberfläche $S$ berechnet wird:
$m = \rho_w S D_E$
Da die Beschleunigung $a$ durch die Corioliskraft mit die Ekmans Geschwindigkeit ($u_e$) erzeugt wird:
$a = \displaystyle\frac{F}{m} =\displaystyle\frac{\sigma_w S}{\rho_w D_E S} = \displaystyle\frac{\sigma_w}{\rho_w D_E} = f u_e$
ergibt sich:
| $ u_e =\displaystyle\frac{ \tau_w }{ f \rho_w D_E }$ |
ID:(11701, 0)
Ekman Transport
Gleichung
Mit die Ekmans Geschwindigkeit ($u_e$) und die Ekmans Tiefe ($D_E$) kann das transportierte Volumen abgeschätzt werden, oder der Ekman Transport ($Q$):
| $ Q = D_E u_e $ |
ID:(11702, 0)