Benützer:
Ozeanbewegung, Zirkulation
Storyboard 
Meeresströmungen werden durch Winde und Änderungen der Wasserdichte erzeugt. Die Coriolis-Kraft beeinflusst diese Wirbel, indem sie die Tiefe, die sie erreichen, verformt und beeinflusst.
ID:(1560, 0)
Derzeitige Generation
Bild
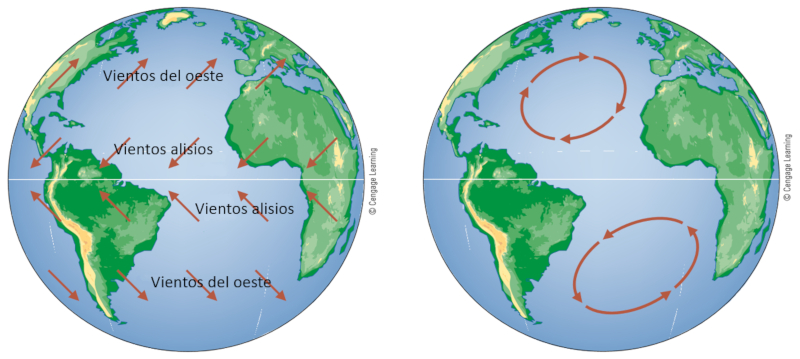
Las corrientes marinas son ageneradas por los vientos de superficie y fluctuaciones de la densidad del agua. El sentido de la circulación es definido por los vientos del oeste (westerlies) y vientos alisios (trade winds), generando circulaciones negativas en el hemisferio norte y positivas en el hemisferio sur.
ID:(11687, 0)
Wärmemischung durch den Wirbel
Bild
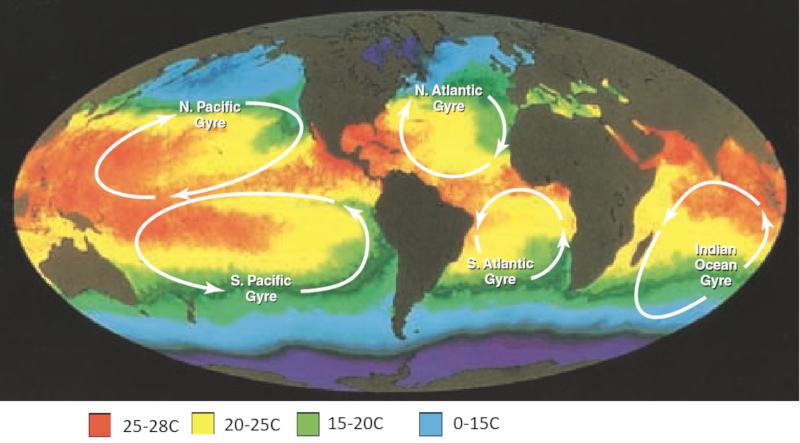
La radiación solar caliente ante todo el océano en latitudes próximas al ecuador. Los vórtices sin embargo pueden arrastrar aguas cálidas hacia los polos y de los polos hacia el ecuador mezclando las aguas cálidas con las frías en las zonas polares.
ID:(11686, 0)
Oberflächenzirkulation in den Ozeanen
Bild
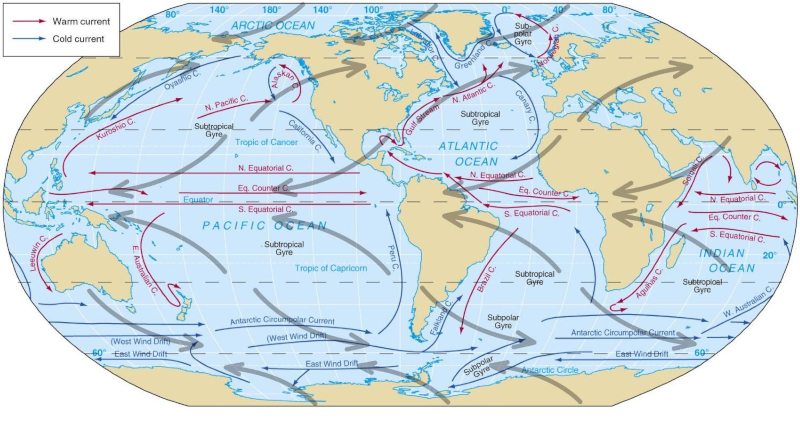
Windinduzierte Zirkulation in der Atmosphäre erzeugt fünf Hauptwirbel: zwei im Pazifik, zwei im Atlantik und einen im Indischen Meer.
Wie vom Coriolis-Gesetz erwartet, drehen sich diese in der nördlichen Hemisphäre in negativer Richtung (wie im Uhrzeigersinn) und positiv in der südlichen Hemisphäre (gegen den Uhrzeigersinn). ).
Sie werden entsprechend der Temperatur, die sie in den äquatorialen und polaren Zonen erfassen, als kalt und heiß klassifiziert.
ID:(11676, 0)
Verformung der Wirbel durch die Coriolis-Kraft
Bild
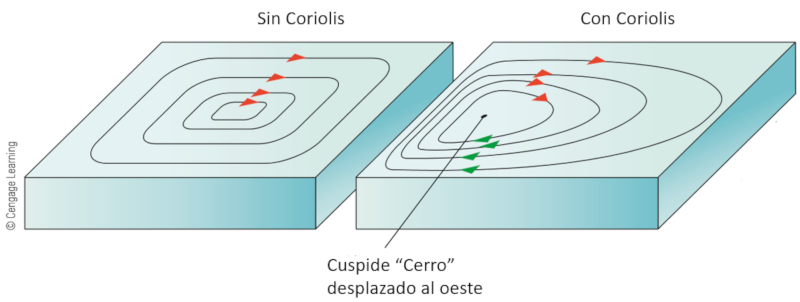
Como la fuerza de Coriolis es nula en el ecuador y crece en dirección de latitudes mayores las corrientes que viajan desde el ecuador hacia los polos tienden a ser angostas. Sin embargo, a medida que se aproximan a los polos, las fuerzas de Coriolis tienden a desviarlas hacia el lado este (hemisferio norte)/oeste (hemisferio sur) de la corriente llevando a un ensanchamiento de la corriente.
Por ello las corrientes que regresan en dirección del ecuador tienden a ser mas anchas, existiendo distorsiones por islas y superficies muy extensas (pacifico).
ID:(11688, 0)
Geringe Wirbelbildung
Bild
En situaciones en que corrientes de distinta temperatura interactuan se forman vórtices mediante la separación de áreas de la corriente principal que por el movimiento relativo de las corrientes giran. Estos vórtices presentan inercia que hace que tiendan a mantener su forma y viajen en una de las corrientes largos recorridos antes de desarmarse.
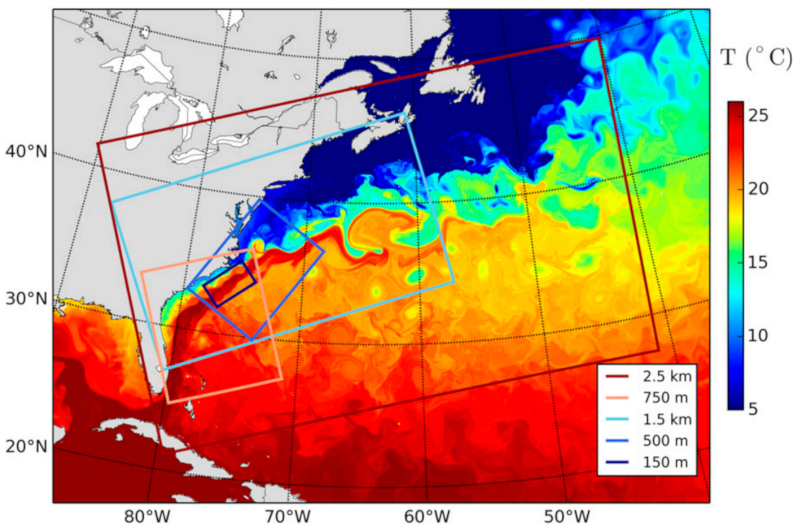
ID:(11677, 0)
Detail der Bildung kleiner Wirbel
Bild
En estas laminas se muestra la formación de vórtices menores en mas detalle:
• dos corrientes interactuando
• por fluctuaciones se forman protuberancias que invaden el área de la otra corriente
• áreas comienzan a girar
• por inercia mantienen la forma e incursionan en la otra corriente
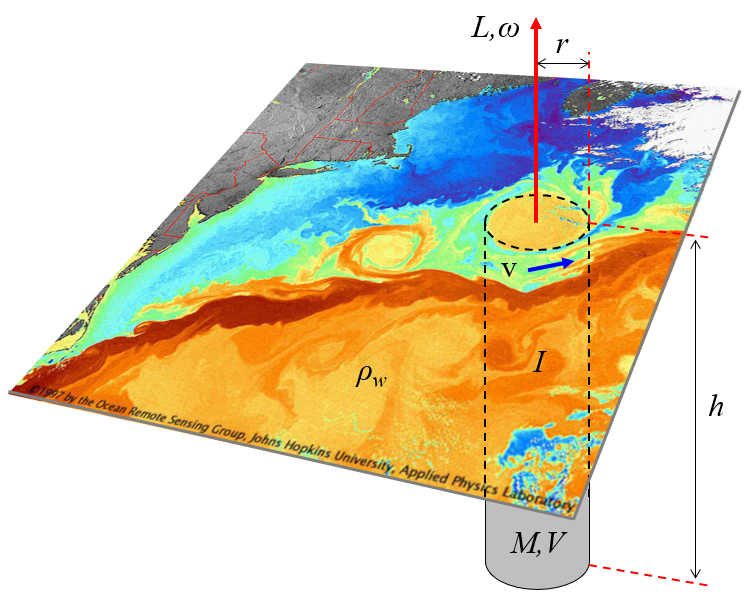
ID:(11678, 0)
Zirkulation von Langmuir in/aus den Tiefen
Bild
Al simplificar las ecuaciones de la ley de Coriolis se obvian movimientos fuera del plano. Sin embargo para movimientos de masas de agua estos si pueden existir y generar aceleraciones hacia la superficie que con es:
| $ a_{c,z} = 2 \omega v_x \cos \varphi$ |
Si se suma a esto la tendencia de que con movimientos hacia el norte en el hemisferio norte existen desplazamientos en la superficie hacia el este se generan circulaciones dentro de una capa de algunos metros. Estas forman verdaderas 'trompas' que se localizan en forma paralela y se van alternando en el sentido de rotación. En los puntos de convergencia se pueden acumular algas y basura creando largas lineas de objetos que flotan.
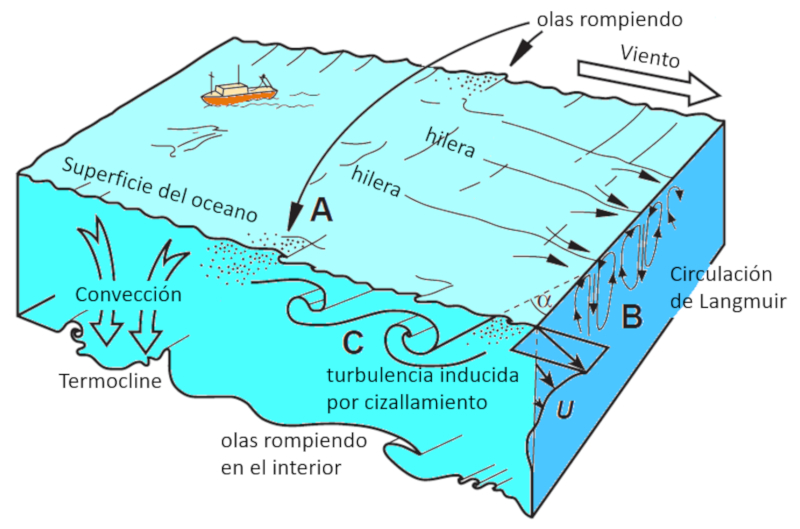
ID:(11681, 0)
Langmuir Zirkulation
Bild
Blick aus der Luft der Langmuir-Zirkulationen: Konvergenzzonen bilden Vertiefungen und Divergenzen bilden Vorsprünge.
ID:(11682, 0)
Oberflächen- und Tiefenzirkulation
Bild
La densidad del agua (efecto de salinidad) genera una parte del flujo se 'hunda' participando en lo que son las corrientes de profundad o 'afloren' y participen en las de superficie.
Como las corrientes de la profundidad no dependen de los vientos no están sujetas a la dinámica de la superficie que se separa por la fuerza de Coriolis en circulación separada por hemisferios.
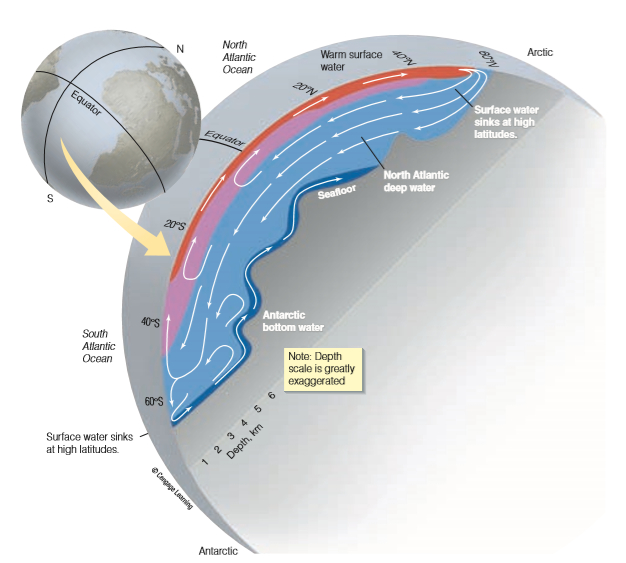
ID:(11690, 0)
Tiefe Zirkulation
Bild
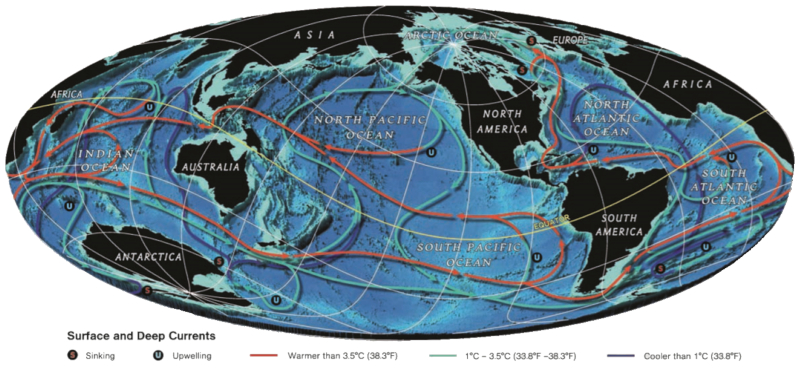
Der tiefe Strom erstreckt sich über den gesamten Globus und verbreitet auch warme und kalte Ströme . Dies hängt von dem Punkt ab, an dem es von Oberflächenströmen gespeist wird:
ID:(11691, 0)
Modell
Top
Parameter
Variablen
Berechnungen
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden 
Gleichungen
$ a_{s,x} = f v_y $
a_sx = f * v_y
$ a_{s,y} = - f v_x $
a_sy = - f * v_x
$ a_{s,z} = e v_x $
a_sz = e * v_x
$ e = 2 \omega \cos \varphi $
e = 2* omega * cos( phi )
$ f = 2 \omega \sin \varphi $
f = 2* omega * sin( phi )
ID:(15444, 0)
Coriolis-Faktor
Gleichung
Um die Gleichungen zu vereinfachen, arbeiten wir mit ein Coriolis-Faktor ($f$)8600,1, was eine Konstante für den physischen Ort ist, da es die Winkelgeschwindigkeit des Planeten ($\omega$)8595 für die Erde und die Breitengrad ($\varphi$)8596 für den Ort einschließt:
| $ f = 2 \omega \sin \varphi $ |
Im südlichen Hemisphäre ist die Breitengrade negativ, und damit 8600, was erklärt, warum Systeme sich in die entgegengesetzte Richtung zum nördlichen Hemisphäre drehen.
ID:(11697, 0)
Zweiter Coriolis-Faktor
Gleichung
Um die Gleichungen zu vereinfachen, arbeiten wir mit ein Zweiter Coriolis-Faktor ($e$)10273,1, was eine Konstante für den physischen Ort ist, da es die Winkelgeschwindigkeit des Planeten ($\omega$)8595 für die Erde und die Breitengrad ($\varphi$)8596 für den Ort einschließt:
| $ e = 2 \omega \cos \varphi $ |
ID:(15450, 0)
Coriolis-Beschleunigung in der Ebene, x-Koordinate
Gleichung
Da sich die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$)8597 mit der Coriolis-Faktor ($f$)8600 umschreiben lässt und unter der Bedingung, dass es keine vertikale Bewegung gibt:
$v_z = 0$
ergibt sich, dass die Coriolis-Beschleunigung an der Oberfläche in x-Richtung ($a_{s,x}$)8601 lautet:
| $ a_{s,x} = f v_y $ |
Da die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$)8597 aus die Winkelgeschwindigkeit des Planeten ($\omega$)8595, die Breitengrad ($\varphi$)8596, die Geschwindigkeit y des Objekt ($v_y$)8513 und die Geschwindigkeit z des Objekt ($v_z$)8594 besteht:
| $ a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi )$ |
und die Definition von der Coriolis-Faktor ($f$)8600 lautet:
| $ f = 2 \omega \sin \varphi $ |
zusätzlich zur Einschränkung der Bewegung auf der Oberfläche, wo:
$v_z = 0$
ergibt sich, dass die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$)8597 ist:
| $ a_{s,x} = f v_y $ |
ID:(11698, 0)
Coriolis-Beschleunigung in der Ebene, y-Koordinate
Gleichung
Da sich die Coriolis-Beschleunigung in x-Richtung ($a_{c,x}$)8597 unter der Bedingung, dass keine vertikale Bewegung vorhanden ist, mit der Coriolis-Faktor ($f$)8600 umschreiben lässt:
$v_z = 0$
Folglich ergibt sich, dass die Coriolis-Beschleunigung an der Oberfläche in y-Richtung ($a_{s,y}$)8602 ist:
| $ a_{s,y} = - f v_x $ |
Da die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$)8598 aus die Winkelgeschwindigkeit des Planeten ($\omega$)8595, die Geschwindigkeit x des Objekt ($v_x$)8512 und die Breitengrad ($\varphi$)8596 besteht:
| $ a_{c,y} = -2 \omega v_x \sin \varphi$ |
und die Definition von der Coriolis-Faktor ($f$)8600 lautet:
| $ f = 2 \omega \sin \varphi $ |
zusätzlich zur Einschränkung der Bewegung auf der Oberfläche, wo gilt:
$v_z = 0$
führt dies dazu, dass die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$)8598 folgendermaßen ist:
| $ a_{s,y} = - f v_x $ |
ID:(11699, 0)
Coriolis-Beschleunigung in der Ebene, z-Koordinate
Gleichung
Da sich die Coriolis-Beschleunigung in z-Richtung ($a_{c,z}$)8599 unter der Bedingung, dass keine vertikale Bewegung vorhanden ist, mit der Zweiter Coriolis-Faktor ($e$)10273 umschreiben lässt:
$v_z = 0$
Folglich ergibt sich, dass die Coriolis-Beschleunigung an der Oberfläche in z-Richtung ($a_{s,z}$)10274 ist:
| $ a_{s,z} = e v_x $ |
Da die Coriolis-Beschleunigung in y-Richtung ($a_{c,y}$)8598 aus die Winkelgeschwindigkeit des Planeten ($\omega$)8595, die Geschwindigkeit x des Objekt ($v_x$)8512 und die Breitengrad ($\varphi$)8596 besteht:
| $ a_{c,y} = -2 \omega v_x \sin \varphi$ |
und die Definition von der Zweiter Coriolis-Faktor ($e$)10273 lautet:
| $ e = 2 \omega \cos \varphi $ |
zusätzlich zur Einschränkung der Bewegung auf der Oberfläche, wo gilt:
$v_z = 0$
führt dies dazu, dass die Coriolis-Beschleunigung an der Oberfläche in z-Richtung ($a_{s,z}$)10274 folgendermaßen ist:
| $ a_{s,z} = e v_x $ |
ID:(15451, 0)