Ocean movement, circulation
Storyboard 
Marine currents are generated by winds and changes in water density. The Coriolis force affects these vortices by deforming and influencing the depth they reach.
ID:(1560, 0)
Current generation
Image 
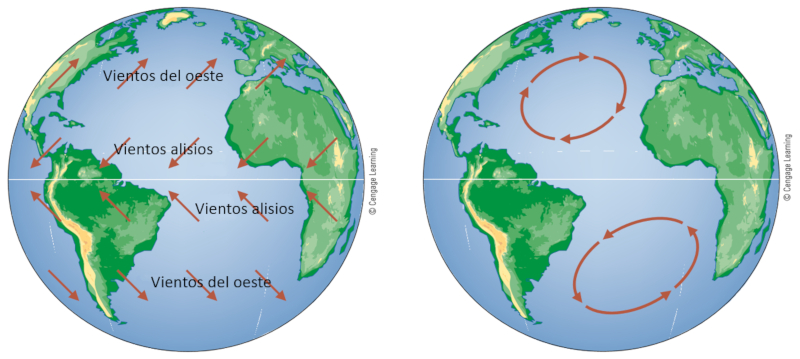
Las corrientes marinas son ageneradas por los vientos de superficie y fluctuaciones de la densidad del agua. El sentido de la circulación es definido por los vientos del oeste (westerlies) y vientos alisios (trade winds), generando circulaciones negativas en el hemisferio norte y positivas en el hemisferio sur.
ID:(11687, 0)
Heat mixing due to the vortices
Image 
La radiación solar caliente ante todo el océano en latitudes próximas al ecuador. Los vórtices sin embargo pueden arrastrar aguas cálidas hacia los polos y de los polos hacia el ecuador mezclando las aguas cálidas con las frías en las zonas polares.
ID:(11686, 0)
Surface circulation in the oceans
Image 
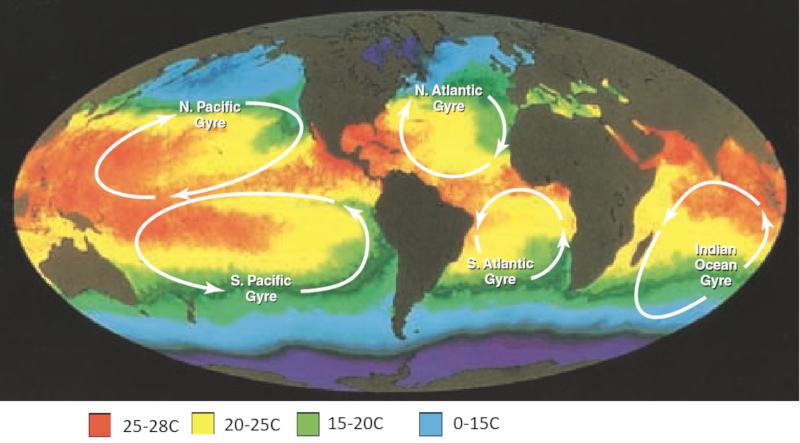
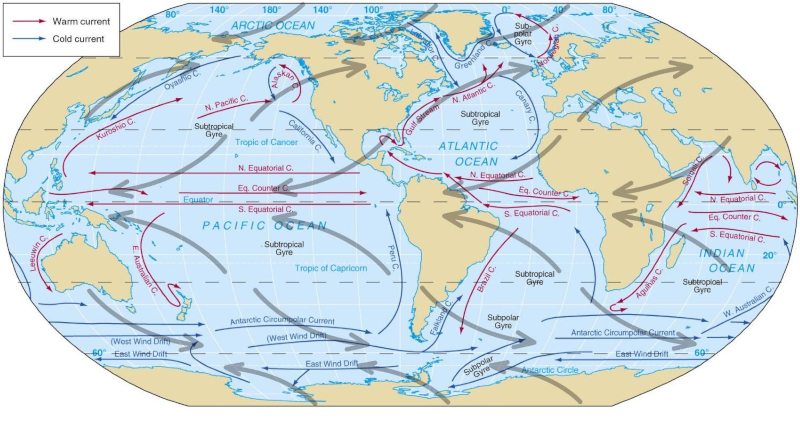
Wind-induced circulation in the atmosphere generates five major vortices: two in the Pacific, two in the Atlantic, and one in the Indian Ocean.
As anticipated by Coriolis law these rotate in the northern hemisphere in the negative direction (clockwise) and positive in the southern hemisphere (counterclockwise) ).
They are classified as cold and hot according to the temperature they are acquiring in the equatorial and polar zones.
ID:(11676, 0)
Deformation of the vortices by the Coriolis force
Image 
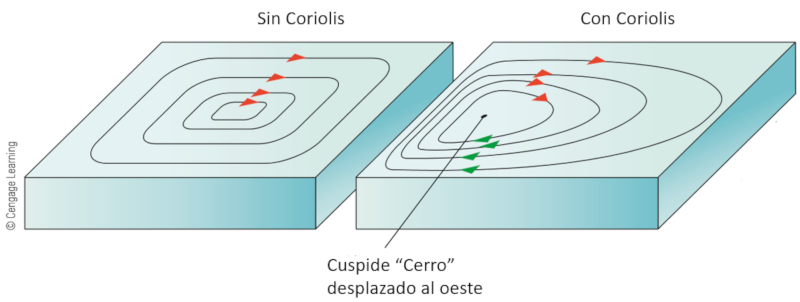
Como la fuerza de Coriolis es nula en el ecuador y crece en dirección de latitudes mayores las corrientes que viajan desde el ecuador hacia los polos tienden a ser angostas. Sin embargo, a medida que se aproximan a los polos, las fuerzas de Coriolis tienden a desviarlas hacia el lado este (hemisferio norte)/oeste (hemisferio sur) de la corriente llevando a un ensanchamiento de la corriente.
Por ello las corrientes que regresan en dirección del ecuador tienden a ser mas anchas, existiendo distorsiones por islas y superficies muy extensas (pacifico).
ID:(11688, 0)
Minor vortex formation
Image 
En situaciones en que corrientes de distinta temperatura interactuan se forman vórtices mediante la separación de áreas de la corriente principal que por el movimiento relativo de las corrientes giran. Estos vórtices presentan inercia que hace que tiendan a mantener su forma y viajen en una de las corrientes largos recorridos antes de desarmarse.
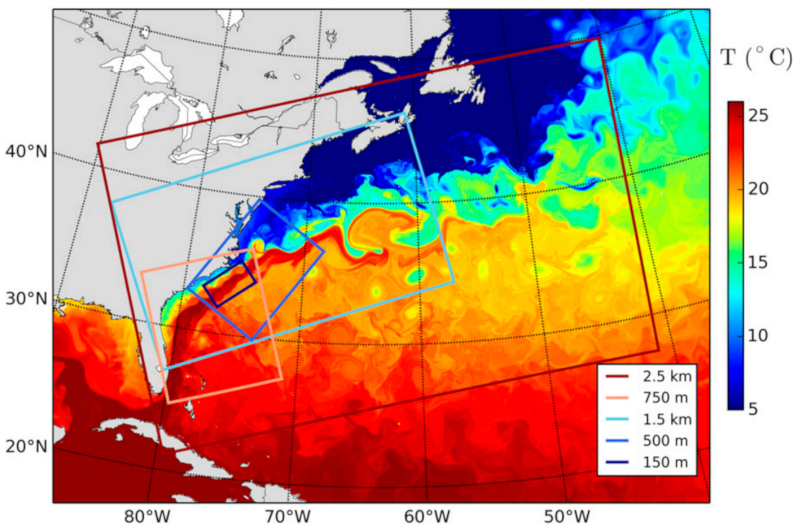
ID:(11677, 0)
Detail of the formation of minor vortices
Image 
En estas laminas se muestra la formación de vórtices menores en mas detalle:
• dos corrientes interactuando
• por fluctuaciones se forman protuberancias que invaden el área de la otra corriente
• áreas comienzan a girar
• por inercia mantienen la forma e incursionan en la otra corriente
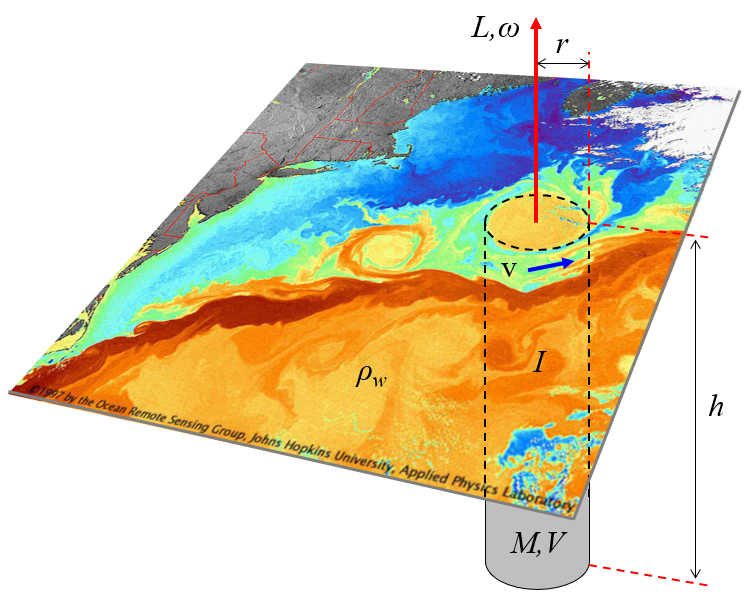
ID:(11678, 0)
Circulation of Langmuir to/from the depths
Image 
Al simplificar las ecuaciones de la ley de Coriolis se obvian movimientos fuera del plano. Sin embargo para movimientos de masas de agua estos si pueden existir y generar aceleraciones hacia la superficie que con es:
| a_{c,z} = 2 \omega v_x \cos \varphi |
Si se suma a esto la tendencia de que con movimientos hacia el norte en el hemisferio norte existen desplazamientos en la superficie hacia el este se generan circulaciones dentro de una capa de algunos metros. Estas forman verdaderas 'trompas' que se localizan en forma paralela y se van alternando en el sentido de rotación. En los puntos de convergencia se pueden acumular algas y basura creando largas lineas de objetos que flotan.
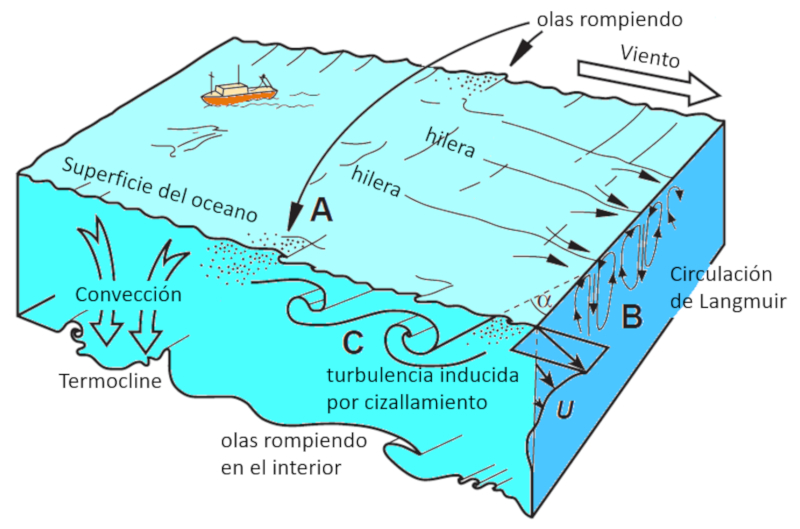
ID:(11681, 0)
Langmuir circulation
Image 
View from the air of Langmuir circulations: convergence zones form depressions and divergences form protrusions.

ID:(11682, 0)
Surface and depth circulation
Image 
La densidad del agua (efecto de salinidad) genera una parte del flujo se 'hunda' participando en lo que son las corrientes de profundad o 'afloren' y participen en las de superficie.
Como las corrientes de la profundidad no dependen de los vientos no están sujetas a la dinámica de la superficie que se separa por la fuerza de Coriolis en circulación separada por hemisferios.
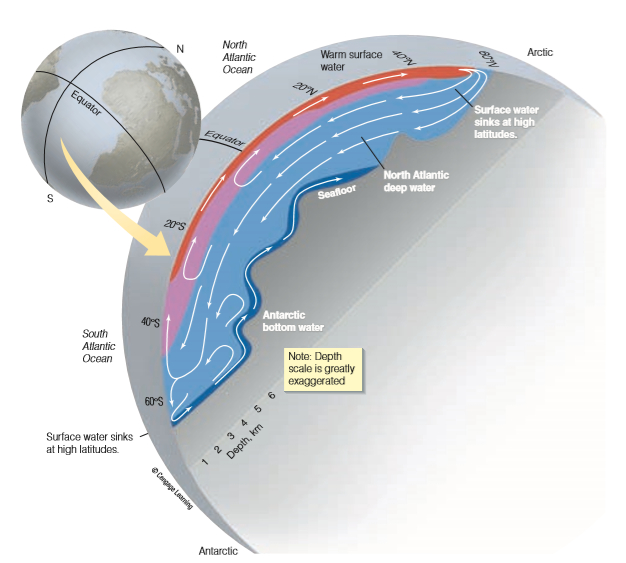
ID:(11690, 0)
Deep circulation
Image 
The deep current extends over the entire globe also spreading warm and cold currents . This depends on the point at which it is fed by surface currents :
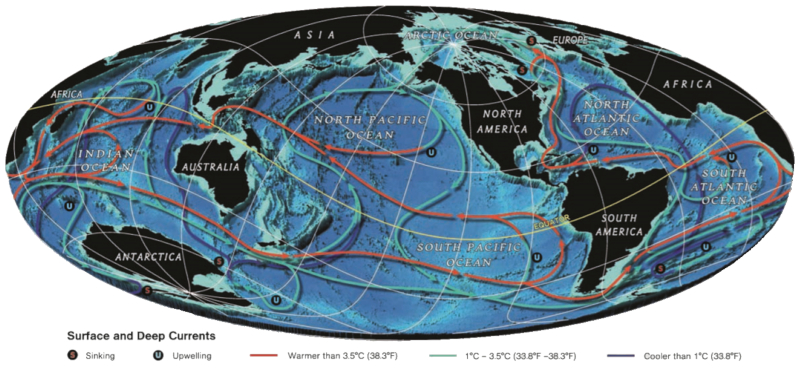
ID:(11691, 0)
Model
Top 
Parameters
Variables
Calculations
Calculations
Calculations
Equations
a_{s,x} = f v_y
a_sx = f * v_y
a_{s,y} = - f v_x
a_sy = - f * v_x
a_{s,z} = e v_x
a_sz = e * v_x
e = 2 \omega \cos \varphi
e = 2* omega * cos( phi )
f = 2 \omega \sin \varphi
f = 2* omega * sin( phi )
ID:(15444, 0)
Coriolis factor
Equation 
To simplify the equations, we work with ($$), which is a constant for the physical location, as it includes the angular velocity of the planet (\omega) for the Earth and the latitude (\varphi) for the location:
In the southern hemisphere, the latitude is negative, and with it, 8600, explaining why systems rotate in the opposite direction to the northern hemisphere.
ID:(11697, 0)
Second Coriolis factor
Equation 
To simplify the equations, we work with ($$), which is a constant for the physical location, as it includes the angular velocity of the planet (\omega) for the Earth and the latitude (\varphi) for the location:
ID:(15450, 0)
Coriolis acceleration in the plane, x coordinate
Equation 
As the coriolis acceleration in x direction (a_{c,x}) can be rewritten with the coriolis factor (f) and under the condition that there is no vertical movement:
v_z = 0
Therefore, it follows that the coriolis acceleration on the surface, in the x direction (a_{s,x}) is:
As the coriolis acceleration in x direction (a_{c,x}) is composed of the angular velocity of the planet (\omega), the latitude (\varphi), the speed y of the object (v_y), and the speed z of the object (v_z):
| a_{c,x} = 2 \omega ( v_y \sin \varphi - v_z \cos \varphi ) |
and the definition of the coriolis factor (f) is:
| f = 2 \omega \sin \varphi |
in addition to the constraint of movement on the surface where:
v_z = 0
this leads to the coriolis acceleration in x direction (a_{c,x}) being:
| a_{s,x} = f v_y |
ID:(11698, 0)
Coriolis acceleration in the plane, y coordinate
Equation 
Since the coriolis acceleration in x direction (a_{c,x}) can be rewritten with the coriolis factor (f) under the condition that there is no vertical movement:
v_z = 0
Then, it follows that the coriolis acceleration on the surface, in the y direction (a_{s,y}) is:
Since the coriolis acceleration in y direction (a_{c,y}) is composed of the angular velocity of the planet (\omega), the speed x of the object (v_x), and the latitude (\varphi):
| a_{c,y} = -2 \omega v_x \sin \varphi |
and the definition of the coriolis factor (f) is:
| f = 2 \omega \sin \varphi |
in addition to the constraint of movement on the surface where:
v_z = 0
this leads to the coriolis acceleration in y direction (a_{c,y}) being:
| a_{s,y} = - f v_x |
ID:(11699, 0)
Coriolis acceleration in the plane, z coordinate
Equation 
Since the coriolis acceleration in z direction (a_{c,z}) can be rewritten with the second Coriolis factor (e) under the condition that there is no vertical movement:
v_z = 0
Then, it follows that the coriolis acceleration on the surface, in the z direction (a_{s,z}) is:
Since the coriolis acceleration in y direction (a_{c,y}) is composed of the angular velocity of the planet (\omega), the speed x of the object (v_x), and the latitude (\varphi):
| a_{c,y} = -2 \omega v_x \sin \varphi |
and the definition of the second Coriolis factor (e) is:
| e = 2 \omega \cos \varphi |
in addition to the constraint of movement on the surface where:
v_z = 0
this leads to the coriolis acceleration on the surface, in the z direction (a_{s,z}) being:
| a_{s,z} = e v_x |
ID:(15451, 0)
