Utilizador:
Troca de momento
Storyboard 
A troca de momento entre a atmosfera e o oceano refere-se ao processo pelo qual a atmosfera impulsiona o oceano, gerando as correspondentes correntes marítimas.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1631, 0)
Tensão superficial
Descrição
O vento sobre a superfície do oceano é composto por um grande número de moléculas que periodicamente colidem com as moléculas de água na superfície.
Dessa forma, parte da energia cinética das moléculas de ar é transferida para as moléculas de água, o que pode ser representado como uma tensão exercida pelo ar sobre a água.
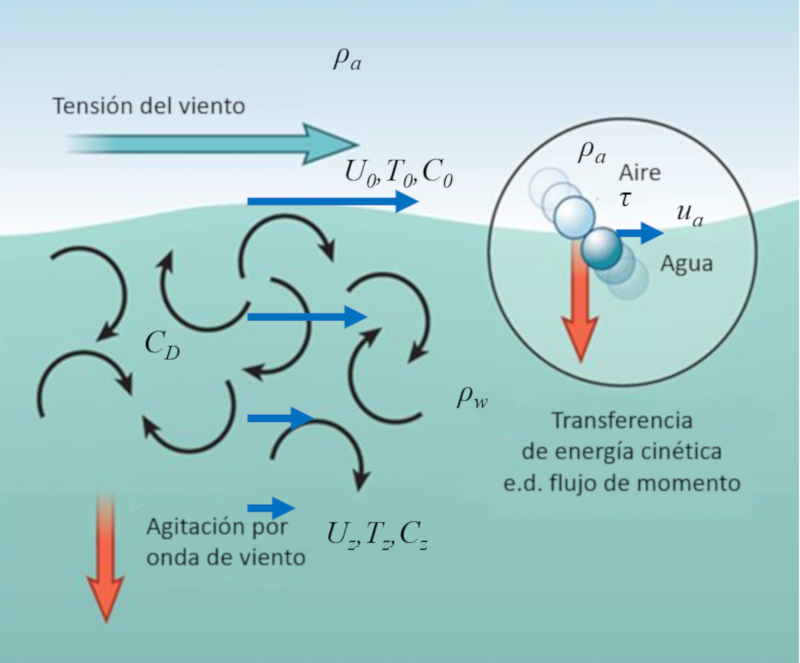
O efeito resultante é a criação de redemoinhos superficiais que, por sua vez, afetam camadas mais profundas, transferindo a velocidade do vento para uma camada superficial do oceano. Isso permite que a energia do vento seja transferida para uma camada próxima à superfície do oceano, aumentando a velocidade da água nessa região.
ID:(12303, 0)
Esquema geral dos tipos de perturbações
Imagem
Geralmente, ao observar o oceano, diversos mecanismos de geração de vórtices e turbulências são evidentes, contribuindo para os processos de mistura.
Dentro da camada superficial, destacam-se:
• Ondas superficiais geradas pelos ventos.
• A circulação de Langmuir, que forma fileiras visíveis do ar.
• O rompimento das ondas superficiais.
Enquanto isso, entre o limite inferior da camada de mistura e a termoclina, características importantes incluem:
• Turbulências devido ao cisalhamento no limite superior.
• Ondas internas quebrando no limite inferior.
• Convecção.
• Instabilidades verticais.
Esses fenômenos são representados no seguinte diagrama:
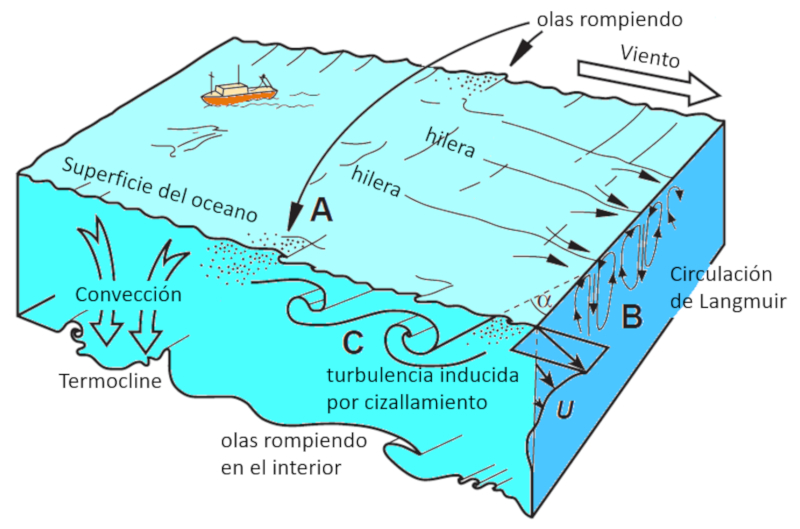
ID:(12180, 0)
Ondas estáveis de Langmuir
Descrição
Um dos fenômenos originados pelas correntes superficiais induzidas pelo vento é a chamada circulação de Langmuir:
Essa circulação se origina de forma semelhante ao transporte de Ekman, em que devido à força de Coriolis, há zonas de afundamento que, ao se afundarem, geram bolhas. A circulação se fecha, criando uma zona de surgência:
No artigo citado na próxima imagem, conclui-se que existem condições para a formação da circulação de Langmuir, as quais dependem das condições e da própria oscilação.
ID:(12221, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ k_w = ( u_a - u_w ) \beta Sc ^ n $
k_w = ( u_a - u_w )* beta * Sc ^ n
$ La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}$
La = sqrt( u_a / u_w )
$ \tau = \tau_t + \tau_w + \tau_{\eta} $
tau = tau_t + tau_w + tau_eta
$ \tau_t = \rho_a C_D ( u_a - u_w )^2$
tau_t = rho_a * C_D * ( u_a - u_w )^2
$ \tau_t = \rho_a u_a ^2 $
tau_t = rho_a * u_a ^2
$ \displaystyle\frac{ u_a ^2 }{ u_w ^2 } = \displaystyle\frac{ \rho_w }{ \rho_a }$
u_a ^2/ u_w ^2 = rho_w / rho_a
ID:(15643, 0)
Perfil de velocidade na camada superficial (MOST)
Equação
A força ($$) exercida sobre a superfície pode ser modelada de acordo com a teoria da similaridade de Monin-Obukhov (MOST) como a transferência de energia cinética do ar para a camada superior do oceano.
Para isso, assume-se que ($$) é proporcional a ($$) e à diferença ao quadrado entre ($$) e ($$). A proporcionalidade é considerada pela introdução de ($$), o que leva à seguinte conclusão:
| $ \tau_t = \rho_a C_D ( u_a - u_w )^2$ |
ID:(12222, 0)
Tensão superficial (MAIS)
Equação
O modelo de Teoria da Similaridade de Monin-Obukhov (MOST) modela a tensão superficial proporcional ao quadrado de ($$) na superfície e a ($$).
Neste caso, estima-se a fração superficial através da densidade de energia cinética, que se correlaciona com a tensão superficial.
Portanto, estima-se que ($$) seja
| $ \tau_t = \rho_a u_a ^2 $ |
ID:(12220, 0)
Tensão total na interface
Equação
O termo ($$) inclui ($$), ($$) e ($$). Portanto, pode ser expresso como:
| $ \tau = \tau_t + \tau_w + \tau_{\eta} $ |
ID:(12232, 0)
Taxa de velocidade
Equação
Se assumirmos que há uma transição contínua na densidade de energia na interface entre o ar e a água, e considerarmos que essa energia é de natureza cinética, então com ($$), ($$) e ($$), ($$) podemos estabelecer a seguinte relação:
$\rho_a u_a^2=\rho_w u_w^2$
Portanto, podemos estabelecer a relação:
| $ \displaystyle\frac{ u_a ^2 }{ u_w ^2 } = \displaystyle\frac{ \rho_w }{ \rho_a }$ |
Além disso, podemos considerar que a densidade de energia tem a mesma unidade que a tensão superficial, o que explica a igualdade em função de que, em um sistema em equilíbrio, as tensões devem ser iguais.
ID:(12234, 0)
Número de Langmuir
Equação
Die Beziehung zwischen ($$) und ($$) wird durch ($$) untersucht. Daher kann die Langmuir-Zahl als das Verhältnis der Quadratwurzel beider Geschwindigkeiten definiert werden:
| $ La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}$ |
ID:(12219, 0)
Troca de CO2, velocidade da água
Equação
O parâmetro do gás la taxa de transferência de gás na água ($k_w$) é descrito em termos de ($$), ($$), o número Schmidt ($Sc$), ($$) e ($$) da seguinte forma:
| $ k_w = ( u_a - u_w ) \beta Sc ^ n $ |
ID:(12215, 0)