Utilizador: 
Quebrando ondas
Storyboard 
As correntes de ar sobre o oceano impulsionam o movimento da água, gerando ondas que se comportam de maneira diferente de acordo com as flutuações na profundidade. Esse fenômeno é conhecido como quebra das ondas. A quebra ocorre porque a velocidade de propagação da onda é maior em áreas de maior profundidade. Assim, à medida que as ondas se aproximam da costa, aquelas de áreas mais profundas tendem a ultrapassar as de áreas mais rasas, resultando na característica quebra da onda.
ID:(1632, 0)
Mecanismos
Iframe
Mecanismos
ID:(15639, 0)
Quebra da onda na praia
Descrição
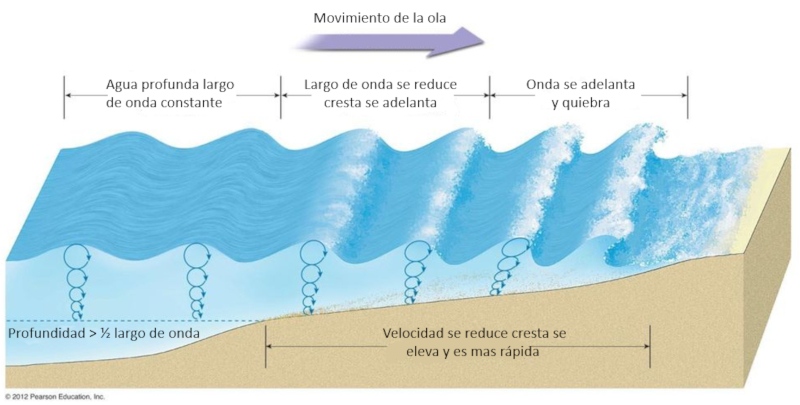
Quando uma onda atinge a praia, ela começa a subir na inclinação da praia, tornando-se progressivamente mais rasa e mais lenta. Uma segunda onda que a segue tende a elevar-se sobre a anterior. Como a água se torna mais profunda nessa situação, a segunda onda é mais rápida e tende a ultrapassar a água que chegou primeiro à praia. Dessa forma, ocorre a quebra da onda.
ID:(12308, 0)
Frequência angular
Conceito
Lembrando que a velocidade angular representa o ângulo percorrido por unidade de tempo, pode-se observar que a expressão
$\displaystyle\frac{2\pi}{T}$
corresponde a uma volta completa ($2\pi$) dividida pelo tempo la período ($T$), necessário para completar um ciclo. Portanto, la frequência angular ($\omega$) é definido como
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(15648, 0)
Vetor de onda
Conceito
O vetor de onda ($k$) é o fator que multiplica a posição e corresponde ao valor para o qual, se a onda se deslocar ao longo de um comprimento de onda ($\lambda$), ela assume a mesma forma que tinha inicialmente. Para que isso ocorra, a seguinte condição deve ser satisfeita:
$kx = k\lambda = 2\pi$
Portanto, com o comprimento de onda ($\lambda$), estabelecemos que:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(15647, 0)
Velocidade de fase de onda
Conceito
A velocidade das ondas depende da profundidade da água e do fator o vetor de onda ($k$), que é calculado usando o comprimento de onda ($\lambda$) da seguinte forma:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
Em relação a o velocidade de fase ($c_p$), que corresponde à velocidade com que cada crista de onda se move, isso pode ser determinado usando o profundidade do oceano ($h$) e la aceleração gravitacional ($g$). O velocidade de fase ($c_p$) é calculado como:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
A velocidade de fase refere-se à velocidade com que uma oscilação ou onda específica se move.
ID:(15649, 0)
Velocidade do grupo de ondas
Conceito
As ondas têm uma velocidade que depende da profundidade da água e do fator o vetor de onda ($k$), calculada usando o comprimento de onda ($\lambda$) da seguinte maneira:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
Para o velocidade do grupo ($c_g$), que representa a velocidade com que o conjunto do trem de ondas se move, e não cada onda individualmente, pode ser calculada utilizando o velocidade de fase ($c_p$). Este é determinado com o profundidade do oceano ($h$) e la aceleração gravitacional ($g$), da seguinte forma:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
Finalmente, utilizando esta informação, o velocidade do grupo ($c_g$) pode ser calculado através da seguinte expressão:
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
A velocidade de grupo é a velocidade com que o trem ou grupo de ondas se desloca no meio aquático.
ID:(15650, 0)
Velocidades das ondas
Imagem
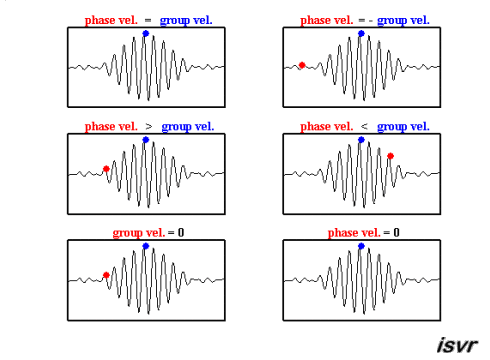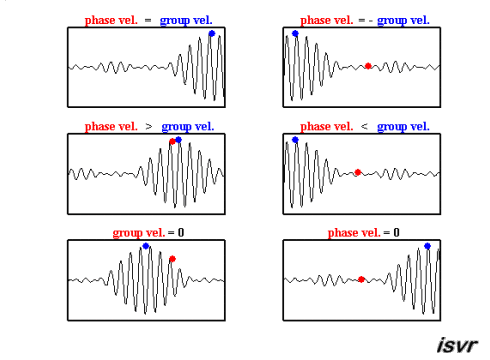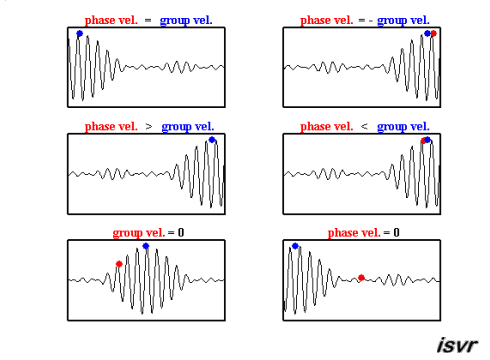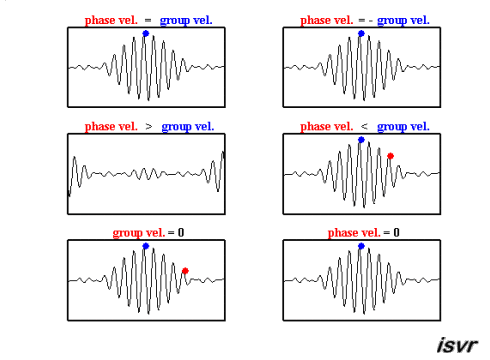
Existem duas velocidades características na mecânica de ondas. Por um lado, temos a velocidade com que uma onda específica se desloca, que pode variar de acordo com a frequência, diferenciando-se, assim, de uma onda para outra.
O segundo tipo de velocidade observada é a de um pacote de ondas, ou seja, um grupo de ondas de diferentes frequências e fases que, ao se superporem, formam um conjunto que se move como uma unidade. Esta velocidade é conhecida como velocidade de grupo.
Ambas podem ser observadas nesta animação:
ID:(15651, 0)
Descrição da onda
Conceito
Uma onda pode ser aproximadamente descrita como uma função senoidal dependendo das variáveis o posição ($x$) e o tempo ($t$).
A função incorpora os valores de o altura da onda ($z$) em cada ponto, bem como o altura máxima da onda ($z_0$), o vetor de onda ($k$) e ($$):
| $ z ( x , t ) = z_0 sin( k x - \omega t )$ |
ID:(15646, 0)
Modelo
Top
Parâmetros
Variáveis
Cálculos
para 
, depois, selecione a variável: 
para 
Cálculos
Cálculos
Variáve 
Dado Calcular 
Objetivo : Equação A ser usado 
Equações
$ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$
c_g = c_p*(1 + 2* k * h / sinh( 2 * k * h ))/2
$ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$
c_p =sqrt( g * tanh( k * h ) / k )
$ k =\displaystyle\frac{2 \pi }{ \lambda }$
k = 2* pi / lambda
$ \omega = \displaystyle\frac{2 \pi }{ T }$
omega = 2* pi / T
$ z ( x , t ) = z_0 sin( k x - \omega t )$
z_xt = z_0 *sin( k * x - omega * t )
ID:(15644, 0)
Descrição da onda
Equação
Uma onda pode ser aproximadamente descrita como uma função senoidal dependendo das variáveis o posição ($x$) e o tempo ($t$).
A função incorpora os valores de o altura da onda ($z$) em cada ponto, bem como o altura máxima da onda ($z_0$), o vetor de onda ($k$) e ($$):
| $ z ( x , t ) = z_0 sin( k x - \omega t )$ |
ID:(12307, 0)
Vetor de onda
Equação
O vetor de onda ($k$) é com o comprimento de onda ($\lambda$) igual a:
| $ k =\displaystyle\frac{2 \pi }{ \lambda }$ |
ID:(12309, 0)
Frequência angular
Equação
La frequência angular ($\omega$) é com la período ($T$) igual a
| $ \omega = \displaystyle\frac{2 \pi }{ T }$ |
ID:(12335, 0)
Velocidade de fase de onda
Equação
O velocidade de fase ($c_p$) corresponde à velocidade com que cada crista de onda se desloca, que pode ser determinada utilizando os valores de o profundidade do oceano ($h$), o comprimento de onda ($\lambda$) e la aceleração gravitacional ($g$). A velocidade o velocidade de fase ($c_p$) é calculada da seguinte forma:
| $ c_p =\sqrt{\displaystyle\frac{ g }{ k } \tanh( k h )}$ |
ID:(12305, 0)
Velocidade do grupo de ondas
Equação
O velocidade do grupo ($c_g$) é calculado utilizando os valores de o vetor de onda ($k$), o profundidade do oceano ($h$) e la aceleração gravitacional ($g$) da seguinte maneira:
| $ c_g =\displaystyle\frac{ c_p }{2}\left(1 + \displaystyle\frac{2 k h }{\sinh(2 k h )}\right)$ |
ID:(12304, 0)