Storyboard

Der Austausch von Impuls zwischen Atmosphäre und Ozean bezieht sich auf den Prozess, bei dem die Atmosphäre den Ozean antreibt und entsprechende Meeresströmungen erzeugt.

Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014

Chapter: Transfer Across the Air-Sea Interface

>Modell

ID:(1631, 0)

Iframe

>Top

ID:(15638, 0)

Beschreibung

>Top

Der Wind über der Meeresoberfläche besteht aus einer großen Anzahl von Molekülen, die regelmäßig auf die Wassermoleküle an der Oberfläche treffen.

Dadurch wird ein Teil der kinetischen Energie der Luftmoleküle auf die Wassermoleküle übertragen, was als eine Art Spannung zwischen Luft und Wasser interpretiert werden kann.

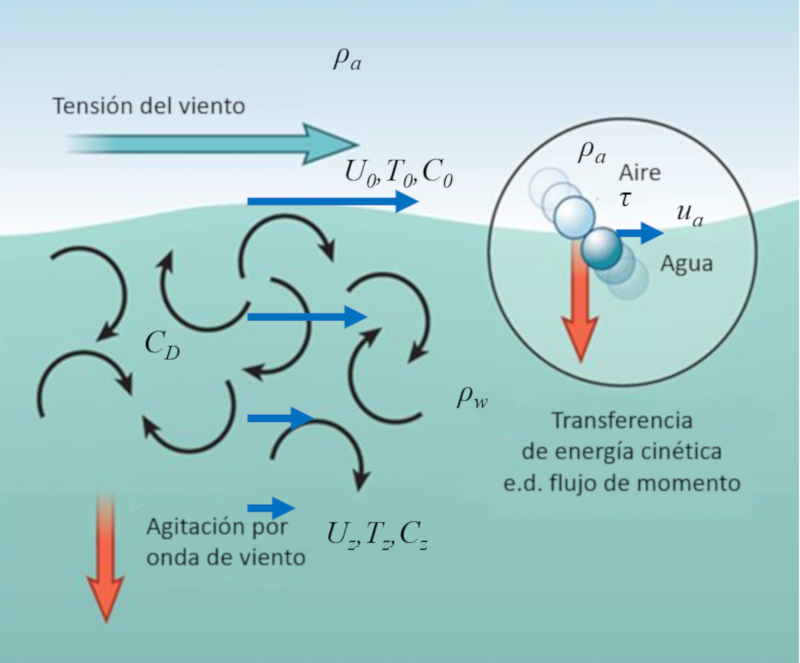
Dies hat zur Folge, dass oberflächliche Wirbel entstehen, die wiederum tiefere Wasserschichten beeinflussen und die Geschwindigkeit des Windes auf eine oberflächennahe Schicht des Ozeans übertragen. Auf diese Weise wird die Bewegungsenergie des Windes in eine oberflächennahe Ozeanschicht übertragen, wodurch die Geschwindigkeit des Wassers erhöht wird.

ID:(12303, 0)

Bild

>Top

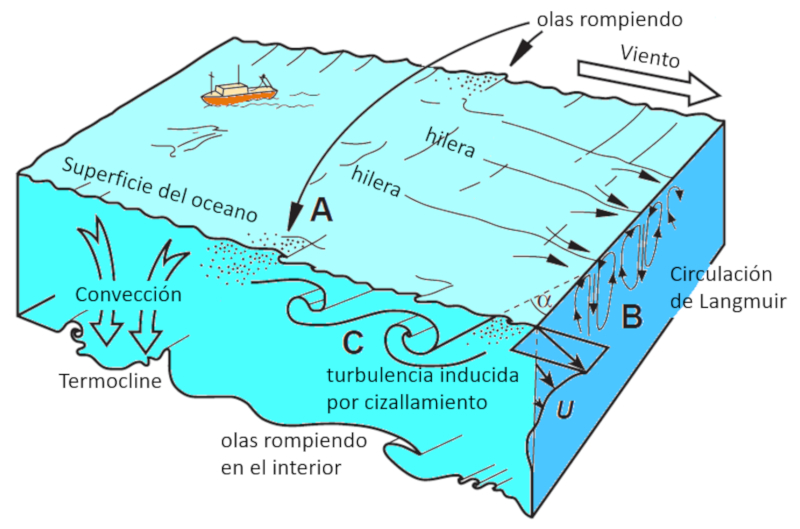
Im Allgemeinen sind beim Betrachten des Ozeans verschiedene Mechanismen erkennbar, die Wirbel und Turbulenzen erzeugen und damit zu den Mischungsprozessen beitragen.

Innerhalb der Oberflächenschicht sind besonders zu erwähnen:

• Oberflächenwellen, die durch Winde erzeugt werden.
• Die Langmuir-Zirkulation, die aus der Luft sichtbare Streifen bildet.
• Das Brechen von Oberflächenwellen.

Während zwischen der unteren Grenze der Mischungsschicht und der Thermokline hervorzuheben sind:

• Turbulenzen durch Scherung an der oberen Grenze.
• Das Brechen interner Wellen an der unteren Grenze.
• Konvektion.
• Vertikale Instabilitäten.

Diese Phänomene sind im folgenden Diagramm dargestellt:

ID:(12180, 0)

Beschreibung

>Top

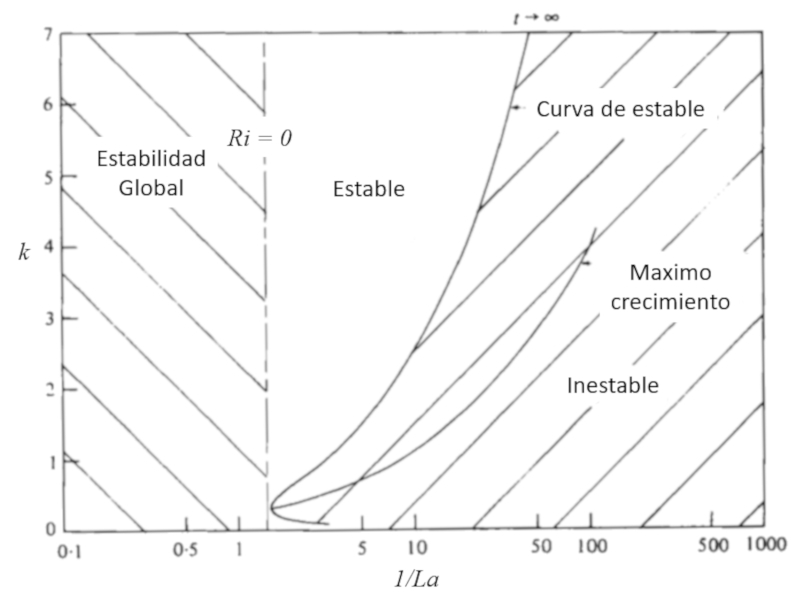
Eines der Phänomene, die durch windinduzierte Oberflächenströmungen entstehen, ist die sogenannte Langmuir-Zirkulation:

The instability of the ocean to Langmuir circulations, S. Leibovich and S. Paoluccit, J. Fluid Mech. (1981). vol. 102, pp. 141-167

Sie entsteht ähnlich wie der Ekman-Transport, bei dem aufgrund der Corioliskraft Gebiete mit Absinken entstehen, die Wirbel erzeugen. Die Zirkulation schließt sich mit der Bildung einer Auftriebszone:

In dem Artikel, der im nächsten Bild zitiert wird, wird geschlussfolgert, dass spezifische Bedingungen für die Bildung der Langmuir-Zirkulation vorliegen, die von verschiedenen Bedingungen und der Oszillation selbst abhängen:

ID:(12221, 0)

Top

>Top

Parameter

$C_D$

C_D

Constante de arrastre

-

$\rho_w$

rho_w

Densidad del agua

kg/m^3

$\rho_a$

rho_a

Densidad del aire

kg/m^3

$n$

n

Exponente de Schmidt

-

$\beta$

beta

Factor beta del transporte aire a agua de CO2

-

$La$

La

Numero de Langmuir

-

$Sc$

Sc

Schmidt-Nummer

-

$\tau_{\eta}$

tau_eta

Tensión de la viscosidad

Pa

$\tau_w$

tau_w

Tensión de las olas

Pa

$\tau_t$

tau_t

Tensión del viento

Pa

$\tau$

tau

Tensión superficial aire-agua

Pa

$u_w$

u_w

Velocidad del agua

m/s

$u_a$

u_a

Velocidad del aire

m/s

Variablen

$k_w$

k_w

Gasübertragungsrate in Wasser

m/s

Berechnungen

• Alternative Methode
• Traditionelle Methode
• Strategie
• 2D
• 3D

Gleichung

Zahl

Zuerst die Gleichung auswählen: zu , dann die Variable auswählen: zu

---

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Berechnungen

Symbol

Gleichung

Gelöst

Übersetzt

Variable Gegeben Berechnen Ziel : Gleichung Zu verwenden

Gleichungen

ID:(15643, 0)

Gleichung

>Top, >Modell

Die Kraft der Tensión del viento ($\tau_t$), die auf der Oberfläche wirkt, kann gemäß der Monin-Obukhov-Ähnlichkeitstheorie (MOST) als Übertragung kinetischer Energie von der Luft auf die obere Schicht des Ozeans modelliert werden.

Dafür wird angenommen, dass der Tensión del viento ($\tau_t$) proportional zu der Densidad del aire ($\rho_a$) und zum Quadratunterschied zwischen der Velocidad del aire ($u_a$) und der Velocidad del agua ($u_w$) ist. Die Proportionalität wird durch die Einführung von der Constante de arrastre ($C_D$) berücksichtigt, was zu folgender Schlussfolgerung führt:

$\tau_t = \rho_a C_D ( u_a - u_w )^2$

Bedingungen

Variablen

$C_D$

Constante de arrastre

$-$

9419

$\rho_a$

Densidad del aire

$kg/m^3$

9418

$\tau_t$

Tensión del viento

$Pa$

9433

$u_w$

Velocidad del agua

$m/s$

9437

$u_a$

Velocidad del aire

$m/s$

9408

Beziehung

ID:(12222, 0)

Gleichung

>Top, >Modell

Die Monin-Obukhov-Ähnlichkeitstheorie (MOST) modelliert die Oberflächenspannung proportional zum Quadrat von der Velocidad del aire ($u_a$) an der Oberfläche und zu der Densidad del aire ($\rho_a$).

In diesem Fall wird der Oberflächenanteil über die Dichte der kinetischen Energie geschätzt, die mit der Oberflächenspannung korreliert.

Daher wird geschätzt, dass der Velocidad del aire ($u_a$) ist

$\tau_t = \rho_a u_a ^2$

Bedingungen

Variablen

$\rho_a$

Densidad del aire

$kg/m^3$

9418

$\tau_t$

Tensión del viento

$Pa$

9433

$u_a$

Velocidad del aire

$m/s$

9408

Beziehung

Entwicklung

None

ID:(12220, 0)

Gleichung

>Top, >Modell

Die Variable der Tensión superficial aire-agua ($\tau$) umfasst der Tensión del viento ($\tau_t$), der Tensión de las olas ($\tau_w$) und der Tensión de la viscosidad ($\tau_{\eta}$). Daher kann sie wie folgt ausgedrückt werden:

$\tau = \tau_t + \tau_w + \tau_{\eta}$

Bedingungen

Variablen

$\tau_{\eta}$

Tensión de la viscosidad

$Pa$

9435

$\tau_w$

Tensión de las olas

$Pa$

9434

$\tau_t$

Tensión del viento

$Pa$

9433

$\tau$

Tensión superficial aire-agua

$Pa$

9417

Beziehung

ID:(12232, 0)

Gleichung

>Top, >Modell

Wenn wir davon ausgehen, dass es einen kontinuierlichen Übergang in der Energiedichte an der Grenzfläche zwischen Luft und Wasser gibt und diese Energie kinetischer Natur ist, dann können wir mit der Densidad del aire ($\rho_a$), der Velocidad del aire ($u_a$) und der Densidad del agua ($\rho_w$), der Velocidad del agua ($u_w$) die folgende Beziehung herleiten:

$\rho_a u_a^2=\rho_w u_w^2$

Daher können wir die Beziehung aufstellen:

$\displaystyle\frac{ u_a ^2 }{ u_w ^2 } = \displaystyle\frac{ \rho_w }{ \rho_a }$

Bedingungen

Variablen

$\rho_w$

Densidad del agua

$kg/m^3$

9438

$\rho_a$

Densidad del aire

$kg/m^3$

9418

$u_w$

Velocidad del agua

$m/s$

9437

$u_a$

Velocidad del aire

$m/s$

9408

Beziehung

Zusätzlich können wir berücksichtigen, dass die Energiedichte dieselbe Einheit wie die Oberflächenspannung hat, was die Gleichheit erklärt, da in einem Gleichgewichtssystem die Spannungen gleich sein müssen.

ID:(12234, 0)

Gleichung

>Top, >Modell

Die Beziehung zwischen der Velocidad del aire ($u_a$) und der Velocidad del agua ($u_w$) wird durch der Numero de Langmuir ($La$) untersucht. Daher kann die Langmuir-Zahl als das Verhältnis der Quadratwurzel beider Geschwindigkeiten definiert werden:

$La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}$

Bedingungen

Variablen

$La$

Numero de Langmuir

$-$

9439

$u_w$

Velocidad del agua

$m/s$

9437

$u_a$

Velocidad del aire

$m/s$

9408

Beziehung

ID:(12219, 0)

Gleichung

>Top, >Modell

Der Gasparameter die Gasübertragungsrate in Wasser ($k_w$) wird in Bezug auf der Velocidad del agua ($u_w$), der Velocidad del aire ($u_a$), der Schmidt-Nummer ($Sc$), der Factor beta del transporte aire a agua de CO2 ($\beta$) und Exponente de Schmidt ($n$) wie folgt beschrieben:

$k_w = ( u_a - u_w ) \beta Sc ^ n$

Bedingungen

Variablen

$n$

Exponente de Schmidt

$-$

9926

$\beta$

Factor beta del transporte aire a agua de CO2

$-$

9409

$k_w$

Gasübertragungsrate in Wasser

$m/s$

9405

$Sc$

Schmidt-Nummer

$-$

9410

$u_w$

Velocidad del agua

$m/s$

9437

$u_a$

Velocidad del aire

$m/s$

9408

Beziehung

ID:(12215, 0)