Échange de moments
Storyboard 
L'échange de moment entre l'atmosphère et l'océan fait référence au processus par lequel l'atmosphère entraîne l'océan, générant les courants océaniques correspondants.
Ocean-Atmosphere Interactions of Gases and Particles, Peter S. Liss, Martin T. Johnson (eds.). Springer, 2014
Chapter: Transfer Across the Air-Sea Interface
ID:(1631, 0)
Tension superficielle
Description 
Le vent sur la surface de l\'océan est composé d\'un grand nombre de molécules qui heurtent périodiquement les molécules d\'eau à la surface.
Ainsi, une partie de l\'énergie cinétique des molécules d\'air est transférée aux molécules d\'eau, ce qui peut être représenté comme une tension exercée par l\'air sur l\'eau.
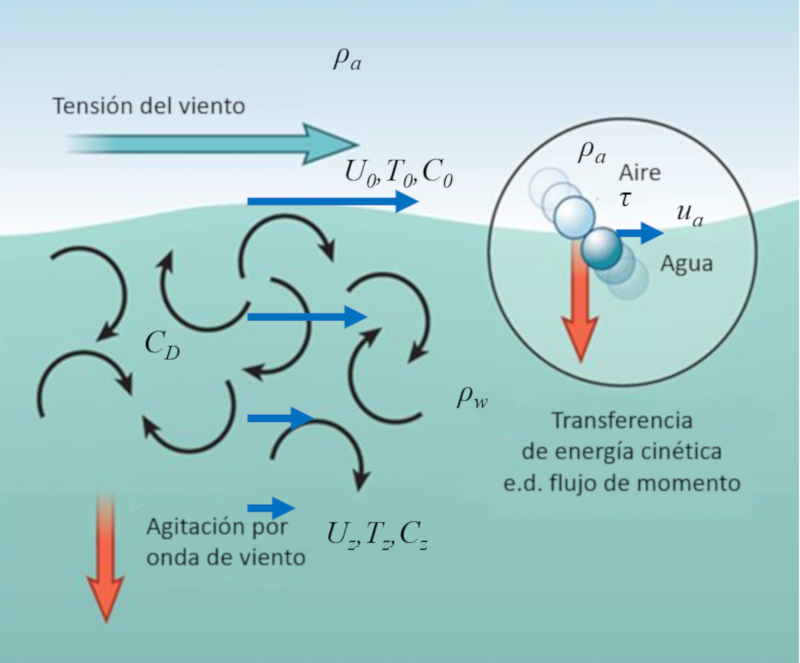
L\'effet résultant est la création de tourbillons superficiels qui, à leur tour, affectent les couches plus profondes, transférant la vitesse du vent à une couche superficielle de l\'océan. Cela permet à l\'énergie du vent d\'être transférée à une couche proche de la surface de l\'océan, augmentant ainsi la vitesse de l\'eau dans cette zone.
ID:(12303, 0)
Schéma général des types de perturbations
Image 
En général, lors de l'observation de l'océan, divers mécanismes de génération de tourbillons et de turbulences sont évidents, contribuant aux processus de mélange.
Au sein de la couche superficielle, les caractéristiques notables incluent :
• Les vagues de surface générées par les vents.
• La circulation de Langmuir, qui forme des rangées visibles depuis les airs.
• La rupture des vagues de surface.
Pendant ce temps, entre la limite inférieure de la couche de mélange et la thermocline, les facteurs importants incluent :
• Les turbulences dues au cisaillement à la limite supérieure.
• Les ondes internes se brisant à la limite inférieure.
• La convection.
• Les instabilités verticales.
Ces phénomènes sont représentés dans le diagramme suivant :
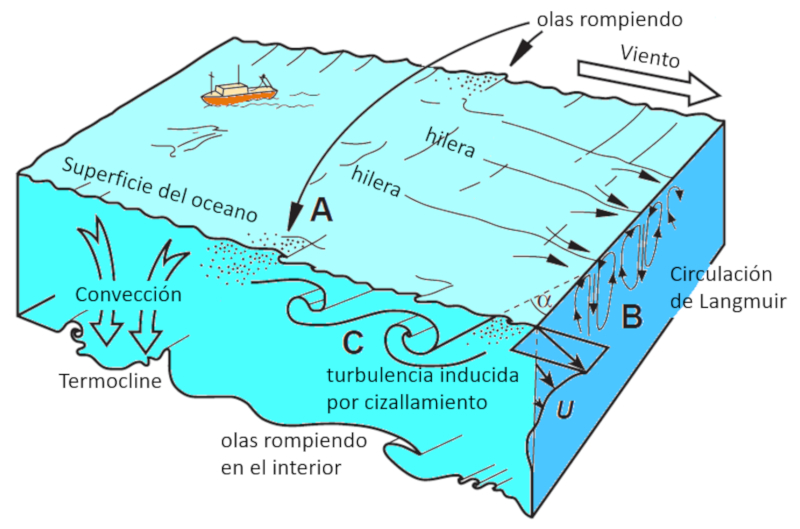
ID:(12180, 0)
Ondes stables de Langmuir
Description 
L'un des phénomènes qui se produit en raison des courants de surface induits par le vent est appelé la circulation de Langmuir :

Celle-ci se forme de manière similaire au transport d'Ekman, où en raison de la force de Coriolis, des zones d'enfoncement se créent, générant des bulles en plongeant. La circulation se ferme, créant ainsi une zone de remontée :

Dans l'article cité dans l'image suivante, il est conclu qu'il existe des conditions pour la formation de la circulation de Langmuir, qui dépendent des conditions et de l'oscillation elle-même.
ID:(12221, 0)
Modèle
Top 
Paramètres
Variables
Calculs
Calculs
Calculs
Équations
k_w = ( u_a - u_w ) \beta Sc ^ n
k_w = ( u_a - u_w )* beta * Sc ^ n
La = \sqrt{\displaystyle\frac{ u_a }{ u_w }}
La = sqrt( u_a / u_w )
\tau = \tau_t + \tau_w + \tau_{\eta}
tau = tau_t + tau_w + tau_eta
\tau_t = \rho_a C_D ( u_a - u_w )^2
tau_t = rho_a * C_D * ( u_a - u_w )^2
\tau_t = \rho_a u_a ^2
tau_t = rho_a * u_a ^2
\displaystyle\frac{ u_a ^2 }{ u_w ^2 } = \displaystyle\frac{ \rho_w }{ \rho_a }
u_a ^2/ u_w ^2 = rho_w / rho_a
ID:(15643, 0)
Profil de vitesse dans la couche superficielle (MOST)
Équation 
La force ($$) exercée sur la surface peut être modélisée selon la théorie de la similitude de Monin-Obukhov (MOST) comme le transfert d'énergie cinétique de l'air à la couche supérieure de l'océan.
Pour ce faire, on suppose que ($$) est proportionnelle à ($$) et à la différence au carré entre ($$) et ($$). Cette proportionnalité est prise en compte par l'introduction de ($$), ce qui conduit à la conclusion suivante :
ID:(12222, 0)
Tension superficielle (LA PLUS)
Équation 
Le modèle de la Théorie de la Similarité de Monin-Obukhov (MOST) modélise la tension superficielle proportionnelle au carré de ($$) à la surface et à ($$).
Dans ce cas, la fraction superficielle est estimée à partir de la densité d'énergie cinétique, qui est corrélée à la tension superficielle.
Ainsi, on estime que ($$) est
ID:(12220, 0)
Tension totale à l'interface
Équation 
Le terme ($$) inclut ($$), ($$) et ($$). Ainsi, il peut être exprimé comme suit :
ID:(12232, 0)
Rapport de vitesse
Équation 
Si nous supposons qu'il y a une transition continue dans la densité d'énergie à l'interface entre l'air et l'eau, et considérons que cette énergie est de nature cinétique, alors avec ($$), ($$) et ($$), ($$), nous pouvons établir la relation suivante :
\rho_a u_a^2=\rho_w u_w^2
Ainsi, nous pouvons établir la relation :
De plus, nous pouvons considérer que la densité d'énergie a la même unité que la tension superficielle, ce qui explique l'égalité en fonction du fait que dans un système en équilibre, les tensions doivent être égales.
ID:(12234, 0)
Nombre de Langmuir
Équation 
La relation entre ($$) et ($$) est étudiée par ($$). Par conséquent, le nombre de Langmuir peut être défini comme le rapport de la racine carrée des deux vitesses :
ID:(12219, 0)
Échange de CO2, vitesse de l'eau
Équation 
Le paramètre du gaz a taux de transfert de gaz dans l'eau (k_w) est décrit en fonction de ($$), ($$), le numéro de Schmidt (Sc), ($$) et ($$) comme suit :
ID:(12215, 0)
