Energía Interna
Storyboard 
La energía interna de un sistema se compone de energía cinética y energía potencial. La energía cinética está relacionada con el calor y puede vincularse a las oscilaciones de los átomos alrededor de sus puntos de equilibrio. Por otro lado, la energía potencial está asociada con el trabajo que el sistema es capaz de realizar.
ID:(1469, 0)
Mecanismos
Concepto 
La energía interna es la energía total contenida dentro de un sistema termodinámico debido a las energías cinética y potencial de sus moléculas. Incluye la energía proveniente del movimiento molecular (traslacional, rotacional y vibracional) y la energía de las interacciones intermoleculares y los enlaces químicos. La energía interna es una función de estado, lo que significa que depende únicamente del estado actual del sistema y no de cómo el sistema alcanzó ese estado. Los cambios en la energía interna ocurren cuando se agrega o se elimina calor del sistema o cuando se realiza trabajo sobre o por el sistema. Este concepto es fundamental en la termodinámica, describiendo los cambios de energía en procesos como los procesos isotérmicos, adiabáticos, isobáricos e isocóricos. La energía interna ayuda a determinar los estados de equilibrio y la estabilidad del sistema, ya que los sistemas tienden a moverse hacia estados con menor energía interna. Proporciona una medida completa de todas las formas microscópicas de energía dentro de un sistema, esencial para entender las transformaciones de energía en diversos procesos.
ID:(15245, 0)
Energía cinetica
Concepto 
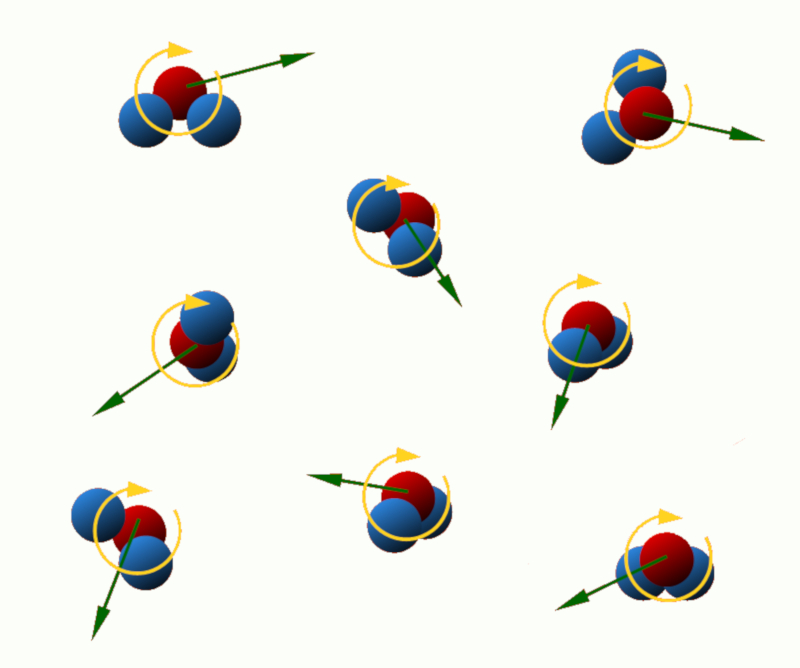
Energía cinética de traslación: Esta energía está asociada al movimiento lineal de las partículas en el sistema. Cuanto mayor sea la velocidad de traslación de las partículas, mayor será su energía cinética de traslación.
Energía cinética de rotación: Algunas partículas, como los átomos o moléculas, pueden rotar alrededor de un eje. Esta rotación está asociada con la energía cinética de rotación, que depende de la masa y la velocidad angular de las partículas.
ID:(11122, 0)
Energía de enlace
Concepto 
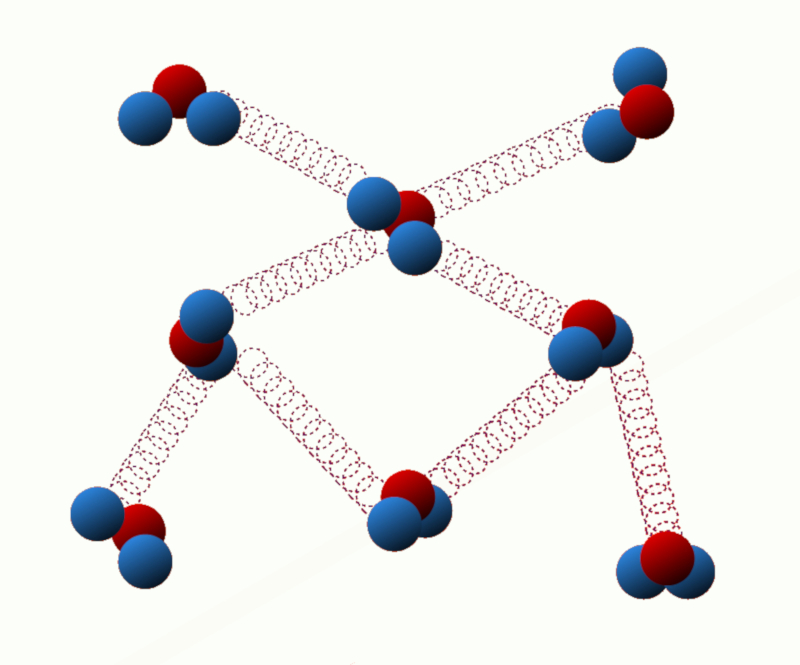
Energía de enlace (energía potencial): Esta energía está relacionada con las fuerzas de interacción entre las partículas del sistema. Por ejemplo, en un sólido, la energía de enlace se debe a las fuerzas de atracción entre los átomos o moléculas vecinos.
ID:(11123, 0)
Energía quimica
Concepto 
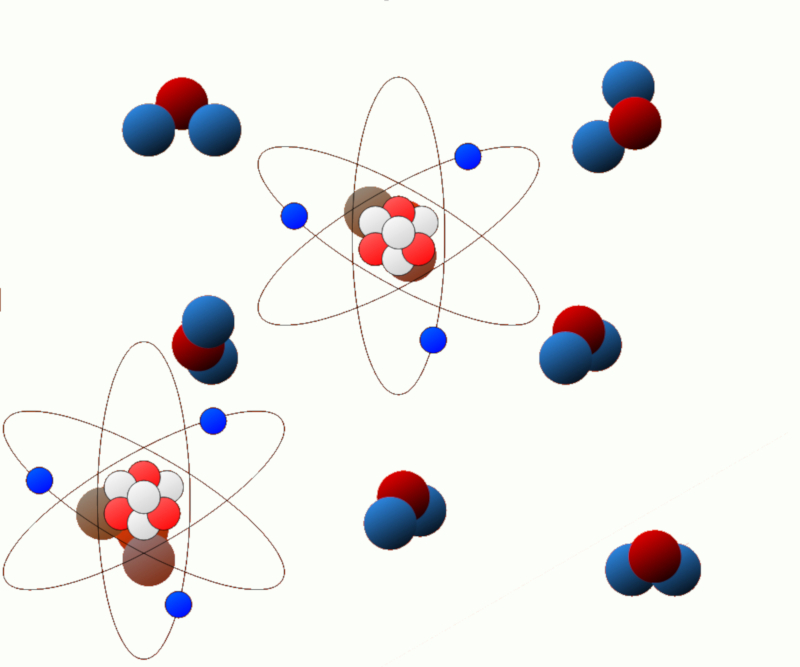
Energía de excitación: Algunos sistemas pueden experimentar cambios en su estado energético, como cuando se excitan los electrones en un átomo o molécula. La energía asociada con estos estados excitados se conoce como energía de excitación.

ID:(11124, 0)
Energía de excitación
Concepto 
Energía química (energía eléctrica): En sistemas químicos, se pueden producir reacciones químicas que liberan o absorben energía. Esta energía se conoce como energía química y está relacionada con los enlaces químicos presentes en las moléculas.
ID:(11125, 0)
Energía interna
Concepto 
La energía interna es la suma total de energía que poseen las partículas que componen un sistema. Estas energías incluyen:• Energía cinética de traslación: Esta energía está asociada al movimiento lineal de las partículas en el sistema. Cuanto mayor sea la velocidad de traslación de las partículas, mayor será su energía cinética de traslación.• Energía cinética de rotación: Algunas partículas, como los átomos o moléculas, pueden rotar alrededor de un eje. Esta rotación está asociada con la energía cinética de rotación, que depende de la masa y la velocidad angular de las partículas.• Energía de enlace (energía potencial): Esta energía está relacionada con las fuerzas de interacción entre las partículas del sistema. Por ejemplo, en un sólido, la energía de enlace se debe a las fuerzas de atracción entre los átomos o moléculas vecinos.• Energía química (energía eléctrica): En sistemas químicos, se pueden producir reacciones químicas que liberan o absorben energía. Esta energía se conoce como energía química y está relacionada con los enlaces químicos presentes en las moléculas.• Energía de excitación: Algunos sistemas pueden experimentar cambios en su estado energético, como cuando se excitan los electrones en un átomo o molécula. La energía asociada con estos estados excitados se conoce como energía de excitación.
ID:(11121, 0)
