Entropía
Storyboard 
La entropía es la porción de energía en un sistema que no puede ser utilizada para realizar trabajo. Desde un punto de vista microscópico, se relaciona con la cantidad de configuraciones posibles que el sistema puede adoptar. Un mayor número de estas configuraciones se vincula con un aumento en el desorden del sistema y una disminución en la probabilidad de que este regrese a un estado previo, reduciendo así la posibilidad de reversibilidad del sistema.
ID:(1471, 0)
Tipos de variables
Imagen 
Si examinamos la ecuación de ERROR:5221,0 con la fuerza mecánica ($F$) y el camino recorrido ($dx$):
| $ \Delta W = F \Delta s $ |
en su forma de la presión ($p$) y el volumen ($V$):
| $ \delta W = p dV $ |
El trabajo desempeña el papel de un potencial, mientras que la presión ($p$) actúa como una 'fuerza generalizada', y el volumen ($V$) sirve como el camino, una especie de 'variable independiente'. Si organizamos estos conceptos en una matriz para los parámetros que hemos discutido hasta ahora, obtenemos:
| Potencial termodinámico | Fuerza generalizada | Variable independiente |
| extensiva | intensiva | extensiva |
| $\delta W$ | $p$ | $dV$ |
| $\delta Q$ | $T$ | $?$ |
En este contexto, observamos que para la línea la variación de calor ($\delta Q$), tenemos la variable la temperatura absoluta ($T$), pero nos falta una variable independiente extensiva. A esto le llamaremos entropía y la denotaremos con la letra $S$.
ID:(11183, 0)
Variables intensivas y extensivas
Nota 
En la física, encontramos variables que se relacionan con cantidades y otras que se relacionan con propiedades.
• Las primeras se conocen como variables extensivas, ya que pueden ser extendidas o aumentadas en proporción a la cantidad de materia presente. Algunos ejemplos de variables extensivas son el volumen, la masa, la carga eléctrica, el calor, entre otros.
• Por otro lado, las segundas se conocen como variables intensivas, las cuales representan propiedades que no dependen de la cantidad de materia presente. Estas propiedades no se alteran al cambiar la cantidad de sustancia. Algunos ejemplos de variables intensivas son la densidad, la presión, la temperatura, entre otras.
ID:(11182, 0)
Entropía y cambio de Fase
Cita 
Si se estima la entropía en función de la temperatura, se observará lo siguiente:
• En cada fase (sólido, líquido, gas), la entropía tiende a aumentar ligeramente con la temperatura.
• En cada cambio de fase, experimenta un salto.
Esto se puede representar de la siguiente manera:

De esta forma, se puede entender la entropía como una medida de los grados de libertad que tiene un sistema. Mientras que en una fase la entropía aumenta gradualmente debido a la liberación de pocos grados de libertad adicionales, en los cambios de fase el incremento es drástico. Un sólido está compuesto por múltiples enlaces que impiden el movimiento de los átomos. En un líquido, se pierden muchos enlaces, lo que crea nuevas libertades que permiten el desplazamiento relativo, asociado a múltiples nuevos grados de libertad. Finalmente, en la transición al estado gaseoso, se pierden todos los enlaces y cada partícula tiene sus tres grados de libertad. Si se incrementa aún más la temperatura, se observa cómo las partículas pueden rotar e incluso oscilar, lo que representa nuevos grados de libertad y mayores incrementos en la entropía.
ID:(11187, 0)
Entropía e Irreversibilidad
Ejercicio 
Si tomamos dos sistemas idénticos, uno con una temperatura $T_1$ y el otro con una temperatura $T_2$, sus entropías se pueden calcular mediante la siguiente ecuación en la que intervienen la entropía ($S$), la temperatura absoluta ($T$), la capacidad Calórica ($C$), la entropía base ($S_0$) y la temperatura base ($T_0$):
| $ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$ |
Por lo tanto, las entropías serán:
$S_1 = S_0 + C\log\left(\displaystyle\frac{T_1}{T_0}\right)$
y
$S_2 = S_0 + C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Si ambos sistemas se mezclan, su temperatura será la temperatura media:
$T_m=\displaystyle\frac{1}{2}(T_1+T_2)$
Por lo tanto, la entropía del nuevo sistema será:
$S_{1+2}=2S_0+2C\log\left(\displaystyle\frac{T_m}{T_0}\right)=2S_0+2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)$
La entropía del nuevo sistema es mayor que la suma de las entropías individuales:
$\Delta S=2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)-C\log\left(\displaystyle\frac{T_1}{T_0}\right)-C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Si representamos gráficamente $\Delta S/C$ en función de $T_1/T_0$ y $T_2/T_0$, obtenemos la siguiente figura:
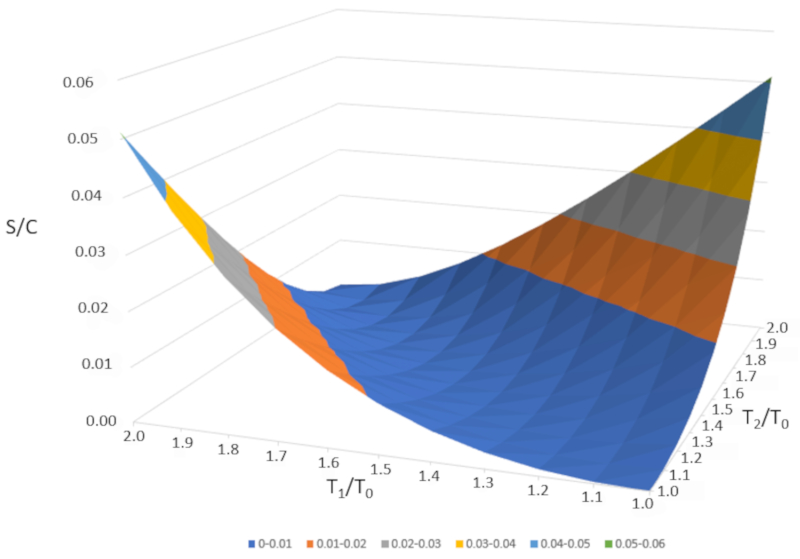
$\Delta S/C$ es casi nulo si las temperaturas son muy similares ($T_1\sim T_2$). Sin embargo, si las temperaturas son diferentes, la entropía siempre aumentará. Si estudiamos esto en otros sistemas, observaremos que cada vez que ocurre un cambio irreversible, la entropía aumenta. La mezcla es irreversible, lo que significa que el sistema no volverá a su estado inicial sin una intervención externa. En otras palabras, el sistema no se separará espontáneamente en dos subsistemas con temperaturas completamente diferentes.
ID:(11186, 0)
Entropía
Descripción 
La entropía física es un concepto fundamental en la termodinámica y la mecánica estadística que representa el grado de desorden o aleatoriedad en un sistema. Mide el número de formas específicas en que un sistema termodinámico puede organizarse, reflejando la cantidad de incertidumbre o el número de posibles microestados correspondientes a un macroestado dado. La entropía cuantifica el desorden, con una entropía mayor indicando un desorden mayor. Según la segunda ley de la termodinámica, la entropía de un sistema aislado nunca disminuye, lo que significa que los procesos naturales tienden a moverse hacia un estado de máxima entropía o desorden. La entropía también mide la irreversibilidad de los procesos, donde los procesos espontáneos aumentan la entropía del universo. Es un factor clave para determinar la eficiencia de motores térmicos y refrigeradores, entender el comportamiento de los sistemas biológicos y estudiar la evolución del universo. En esencia, la entropía es una medida de la imprevisibilidad y la dispersión de la energía en un sistema, proporcionando información sobre la tendencia natural hacia el desorden y las limitaciones de la conversión de energía.
Variables
Cálculos
Cálculos
Ecuaciones
Ejemplos
Para comprender mejor el concepto de entrop a, podemos imaginar un sistema en estado s lido, donde los tomos est n organizados de manera ordenada y la entrop a es baja.
A medida que se suministra energ a al sistema, los tomos comienzan a oscilar con mayor amplitud y el orden se reduce progresivamente. Al alcanzar la temperatura de fusi n, algunas part culas se liberan de sus posiciones fijas y adquieren mayor libertad de movimiento dentro de la matriz del material, lo que introduce un grado mayor de desorden. Este incremento del desorden implica un aumento de la entrop a.
Al seguir aportando energ a y alcanzar la temperatura de ebullici n, las part culas comienzan a escapar del sistema, transform ndose en gas. Este estado es el de mayor libertad y desorden molecular, y por tanto, el de mayor entrop a. Finalmente, cuando el sistema se evapora por completo, se alcanza un nivel m ximo de entrop a dentro de esta transformaci n.
(ID 15246)
Si examinamos la ecuaci n de ERROR:5221,0 con la fuerza mecánica ($F$) y el camino recorrido ($dx$):
| $ \Delta W = F \Delta s $ |
en su forma de la presión ($p$) y el volumen ($V$):
| $ \delta W = p dV $ |
El trabajo desempe a el papel de un potencial, mientras que la presión ($p$) act a como una 'fuerza generalizada', y el volumen ($V$) sirve como el camino, una especie de 'variable independiente'. Si organizamos estos conceptos en una matriz para los par metros que hemos discutido hasta ahora, obtenemos:
| Potencial termodin mico | Fuerza generalizada | Variable independiente |
| extensiva | intensiva | extensiva |
| $\delta W$ | $p$ | $dV$ |
| $\delta Q$ | $T$ | $?$ |
En este contexto, observamos que para la l nea la variación de calor ($\delta Q$), tenemos la variable la temperatura absoluta ($T$), pero nos falta una variable independiente extensiva. A esto le llamaremos entrop a y la denotaremos con la letra $S$.
(ID 11183)
En la f sica, encontramos variables que se relacionan con cantidades y otras que se relacionan con propiedades.
• Las primeras se conocen como variables extensivas, ya que pueden ser extendidas o aumentadas en proporci n a la cantidad de materia presente. Algunos ejemplos de variables extensivas son el volumen, la masa, la carga el ctrica, el calor, entre otros.
• Por otro lado, las segundas se conocen como variables intensivas, las cuales representan propiedades que no dependen de la cantidad de materia presente. Estas propiedades no se alteran al cambiar la cantidad de sustancia. Algunos ejemplos de variables intensivas son la densidad, la presi n, la temperatura, entre otras.
(ID 11182)
Si se estima la entrop a en funci n de la temperatura, se observar lo siguiente:
• En cada fase (s lido, l quido, gas), la entrop a tiende a aumentar ligeramente con la temperatura.
• En cada cambio de fase, experimenta un salto.
Esto se puede representar de la siguiente manera:

De esta forma, se puede entender la entrop a como una medida de los grados de libertad que tiene un sistema. Mientras que en una fase la entrop a aumenta gradualmente debido a la liberaci n de pocos grados de libertad adicionales, en los cambios de fase el incremento es dr stico. Un s lido est compuesto por m ltiples enlaces que impiden el movimiento de los tomos. En un l quido, se pierden muchos enlaces, lo que crea nuevas libertades que permiten el desplazamiento relativo, asociado a m ltiples nuevos grados de libertad. Finalmente, en la transici n al estado gaseoso, se pierden todos los enlaces y cada part cula tiene sus tres grados de libertad. Si se incrementa a n m s la temperatura, se observa c mo las part culas pueden rotar e incluso oscilar, lo que representa nuevos grados de libertad y mayores incrementos en la entrop a.
(ID 11187)
Si tomamos dos sistemas id nticos, uno con una temperatura $T_1$ y el otro con una temperatura $T_2$, sus entrop as se pueden calcular mediante la siguiente ecuaci n en la que intervienen la entropía ($S$), la temperatura absoluta ($T$), la capacidad Calórica ($C$), la entropía base ($S_0$) y la temperatura base ($T_0$):
| $ S = S_0 + C \log\left(\displaystyle\frac{ T }{ T_0 }\right)$ |
Por lo tanto, las entrop as ser n:
$S_1 = S_0 + C\log\left(\displaystyle\frac{T_1}{T_0}\right)$
y
$S_2 = S_0 + C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Si ambos sistemas se mezclan, su temperatura ser la temperatura media:
$T_m=\displaystyle\frac{1}{2}(T_1+T_2)$
Por lo tanto, la entrop a del nuevo sistema ser :
$S_{1+2}=2S_0+2C\log\left(\displaystyle\frac{T_m}{T_0}\right)=2S_0+2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)$
La entrop a del nuevo sistema es mayor que la suma de las entrop as individuales:
$\Delta S=2C\log\left(\displaystyle\frac{T_1+T_2}{2T_0}\right)-C\log\left(\displaystyle\frac{T_1}{T_0}\right)-C\log\left(\displaystyle\frac{T_2}{T_0}\right)$
Si representamos gr ficamente $\Delta S/C$ en funci n de $T_1/T_0$ y $T_2/T_0$, obtenemos la siguiente figura:

$\Delta S/C$ es casi nulo si las temperaturas son muy similares ($T_1\sim T_2$). Sin embargo, si las temperaturas son diferentes, la entrop a siempre aumentar . Si estudiamos esto en otros sistemas, observaremos que cada vez que ocurre un cambio irreversible, la entrop a aumenta. La mezcla es irreversible, lo que significa que el sistema no volver a su estado inicial sin una intervenci n externa. En otras palabras, el sistema no se separar espont neamente en dos subsistemas con temperaturas completamente diferentes.
(ID 11186)
(ID 15305)
ID:(1471, 0)
