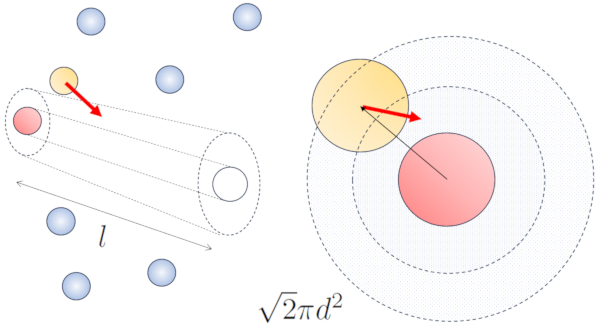
Quando part culas vizinhas est o em movimento, h uma maior probabilidade de colis o devido ao fato de que elas percorrem uma dist ncia maior no mesmo intervalo de tempo. As componentes de velocidade, $v_x$, $v_y$ e $v_z$, flutuam em torno de valores m dios $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ e $\sqrt{\langle v_z^2\rangle}$. Supondo que o sistema seja isotr pico, a m dia de cada componente ser igual a $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Portanto, ao longo do eixo ao qual a part cula est se movendo, ela percorrer uma dist ncia

$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$

Ao mesmo tempo, as part culas que se movem perpendicularmente ter o percorrido uma dist ncia:

$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$

Portanto, a probabilidade de colis o aumenta em um fator de $\sqrt{2}$ em compara o com o caso em que as part culas n o est o em movimento:

image

O caminho m dio livre pode ser estimado em termos do di metro de um cilindro imagin rio que envolve uma part cula, em m dia, tendo uma colis o com outra part cula.

O raio do cilindro corresponde dist ncia m xima que duas part culas devem ter para colidir, o que equivale a duas vezes o raio da part cula, ou seja, o diâmetro de partícula ($d$). Como apenas uma colis o ocorre dentro deste cilindro, o n mero de part culas contidas nele deve ser igual a um. Isso significa que:

$l d^2\pi c_n= 1$

com la concentração de partículas ($c_n$), e resolvendo para o camino livre ($\bar{l}$), obtemos:

kyon

Isso representa o caminho m dio livre.

Uma vez que o di metro da part cula $d$ o dobro do raio $a$

$d=2a$

e a concentra o de part culas $c_N$ pode ser expressa em termos de concentra o molar $c_n$ como

$c_N=N_Ac_n$

onde $N_A$ o n mero de Avogadro, a equa o para o caminho livre m dio

$l=\displaystyle\frac{1}{4a^2\pi c_N}$

tamb m pode ser escrita como:

kyon

Quando uma part cula de um g s se move, ela interage com outras part culas. A forma mais simples dessa intera o atrav s de colis es el sticas, o que significa que a part cula colide sem perder energia, mudando sua dire o para impactar outra part cula.

imagem

Dentro desse processo, faz sentido definir o camino livre ($\bar{l}$), cujo valor depender de uma concentração de partículas ($c_n$).

Quando uma mol cula se move periodicamente atrav s do volume que cont m o g s, eventualmente ela encontrar outra mol cula e poder ocorrer uma colis o. A dist ncia que ela percorre entre duas colis es consecutivas chamada de 'caminho livre m dio'.

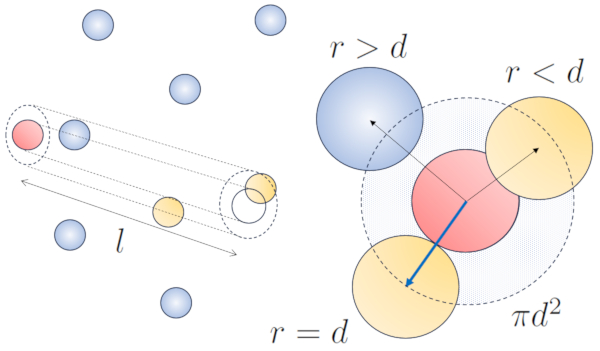
Quando uma part cula com um raio dado se move pelo espa o, ela efetivamente ocupa o espa o de um cilindro com o mesmo raio. Para que uma part cula colida com outra, a segunda deve ter parte de seu volume dentro desse cilindro. No caso mais extremo, a segunda part cula est localizada a uma dist ncia de dois raios da primeira, de modo que a borda do cilindro toca um ponto na esfera mais pr xima ao eixo do cilindro. O centro dessa esfera est a uma dist ncia igual a um raio da superf cie do cilindro:

image

Portanto, a dist ncia entre o eixo do cilindro e o centro de qualquer part cula de dois raios, ou seja, um di metro. Em ess ncia, pode-se imaginar que o volume ocupado literalmente pela part cula que se desloca pelo espa o um cilindro com um comprimento igual ao caminho livre e um raio igual ao di metro da pr pria part cula.

Se dividirmos la densidade ($\rho$) por la massa molar ($m$), obteremos la concentração de partículas ($c_n$):

kyon

Para converter a la concentração molar ($c_m$) em la concentração de partículas ($c_n$), basta multiplicar a primeira por o número de Avogrado ($N_A$), assim:

kyon

La concentração molar ($c_m$) corresponde a ERROR:9339,0 dividido por o volume ($V$) de um g s e calculado da seguinte forma:

kyon

No caso sem movimento, a probabilidade de o camino livre ($\bar{l}$), enquanto com movimento, as probabilidades s o de o diâmetro de partícula ($d$) e la concentração de partículas ($c_n$), respectivamente.

equa o=3942

No caso de movimento, a probabilidade aumenta em um fator de $\sqrt{2}$, o que significa que o caminho livre

kyon

mechanisms

model