Puisque le diam tre de la particule $d$ est le double du rayon $a$

$d=2a$

et que la concentration de particules $c_N$ peut tre exprim e en termes de concentration molaire $c_n$ comme

$c_N=N_Ac_n$

o $N_A$ est le nombre d'Avogadro, l' quation pour le libre parcours moyen

$l=\displaystyle\frac{1}{4a^2\pi c_N}$

peut galement tre crite comme :

kyon

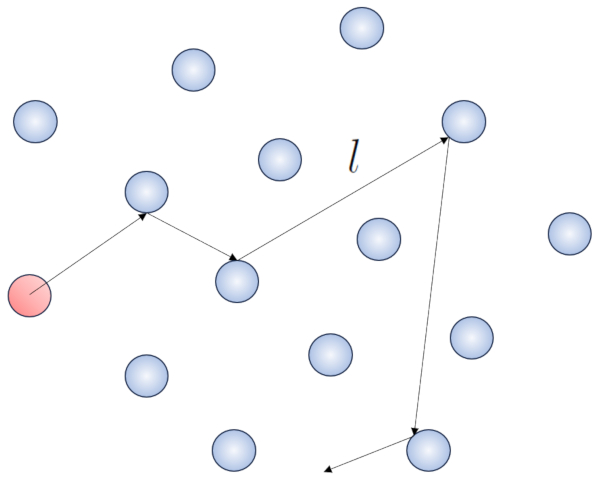
Lorsqu'une mol cule se d place p riodiquement travers le volume contenant le gaz, elle finira par rencontrer une autre mol cule et elles pourront entrer en collision. La distance parcourue entre deux collisions cons cutives est appel e le 'libre parcours moyen'.

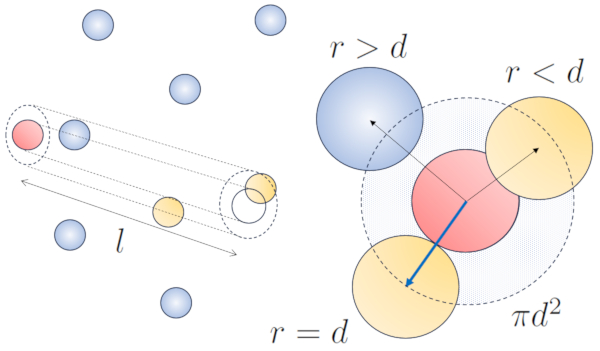
Lorsqu'une particule dot e d'un rayon donn se d place dans l'espace, elle occupe effectivement l'espace d'un cylindre avec le m me rayon. Pour qu'une particule entre en collision avec une autre, la seconde doit avoir une partie de son volume l'int rieur de ce cylindre. Dans le cas le plus extr me, la deuxi me particule se trouve une distance de deux rayons de la premi re, de sorte que le bord du cylindre touche un point de la sph re le plus proche de l'axe du cylindre. Le centre de cette sph re est situ une distance gale un rayon de la surface du cylindre :

image

Par cons quent, la distance entre l'axe du cylindre et le centre de n'importe quelle particule est de deux rayons, autrement dit, un diam tre. En essence, on peut imaginer que le volume litt ralement occup par la particule se d pla ant dans l'espace est un cylindre ayant une longueur gale au libre parcours et un rayon gal au diam tre de la particule elle-m me.

Si nous divisons a densité ($\rho$) par a masse molaire ($m$), nous obtiendrons a concentration de particules ($c_n$) :

kyon

Pour convertir a concentration molaire ($c_m$) en a concentration de particules ($c_n$), il suffit de multiplier la premi re par le numéro d'Avogadro ($N_A$), comme suit :

kyon

A concentration molaire ($c_m$) correspond ERROR:9339,0 divis par le volume ($V$) d'un gaz et est calcul comme suit :

kyon

La longueur libre moyenne peut tre estim e en fonction du diam tre d'un cylindre imaginaire entourant une particule, en moyenne ayant une collision avec une autre particule.

Le rayon du cylindre correspond la distance maximale que deux particules doivent avoir pour entrer en collision, ce qui quivaut deux fois le rayon de la particule, c'est- -dire le diamètre des particules ($d$). Comme seule une collision se produit l'int rieur de ce cylindre, le nombre de particules qu'il contient doit tre gal un. Cela signifie que :

$l d^2\pi c_n= 1$

avec a concentration de particules ($c_n$), et en r solvant pour le route libre ($\bar{l}$), nous obtenons :

kyon

Cela repr sente la longueur libre moyenne.

mechanisms

model

Dans le cas sans mouvement, la probabilit est de le route libre ($\bar{l}$), tandis qu'avec le mouvement, les probabilit s sont de le diamètre des particules ($d$) et a concentration de particules ($c_n$), respectivement.

quation=3942

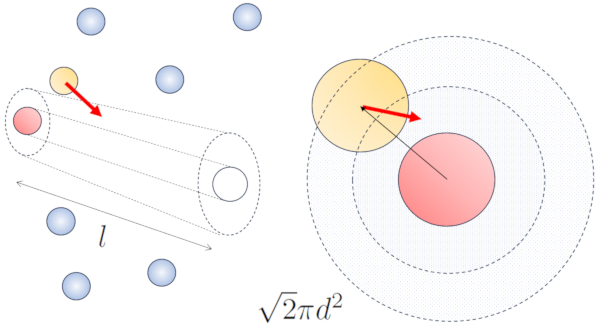
Dans le cas du mouvement, la probabilit augmente d'un facteur de $\sqrt{2}$, ce qui signifie que le chemin libre est

kyon

Lorsque des particules voisines sont en mouvement, il existe une probabilit plus lev e de collision en raison du fait qu'elles parcourent une plus grande distance en m me temps. Les composantes de vitesse, $v_x$, $v_y$ et $v_z$, fluctuent autour de valeurs moyennes $\sqrt{\langle v_x^2\rangle}$, $\sqrt{\langle v_y^2\rangle}$ et $\sqrt{\langle v_z^2\rangle}$. En supposant que le syst me soit isotrope, la moyenne de chaque composante sera gale $\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}$. Par cons quent, le long de l'axe le long duquel la particule se d place, elle parcourra une distance

$\sqrt{\langle v_z^2\rangle}dt=\displaystyle\frac{1}{3}\sqrt{\langle v^2\rangle}dt$

En m me temps, les particules se d pla ant perpendiculairement auront parcouru une distance :

$\sqrt{\langle v_x^2\rangle+\langle v_y^2\rangle}dt=\displaystyle\frac{\sqrt{2}}{3}\sqrt{\langle v^2\rangle}dt$

Ainsi, la probabilit de collision augmente d'un facteur de $\sqrt{2}$ par rapport au cas o les particules ne sont pas en mouvement :

image

Quand une particule d'un gaz se d place, elle interagit avec les autres particules. La forme la plus simple de cette interaction se produit travers des collisions lastiques, ce qui signifie que la particule entre en collision sans perdre d' nergie, changeant sa direction pour ensuite entrer en collision avec une autre particule.

image

Dans ce processus, il est judicieux de d finir le route libre ($\bar{l}$), dont la valeur d pendra de une concentration de particules ($c_n$).