Conducción térmica
Storyboard 
El transporte de calor consiste en dos procesos que se alternan. Por un lado, está la conducción a través de un medio y, por el otro, la transmisión de calor de un medio a otro.El transporte a través de un medio implica la transferencia de calor al medio, seguida de la conducción a través del mismo y, finalmente, la transmisión del calor fuera del medio. En medios más complejos, se deben considerar múltiples etapas de conducción y transmisión entre diferentes medios. Si el calor se genera o se absorbe en uno de los medios, se toma en cuenta la conducción desde o hacia esa fuente o sumidero de calor.
ID:(313, 0)
Mecanismo de conducción de calor
Concepto 
Para comprender como se conduce calor en un solido o liquido debemos imaginar que este esta compuesto por particulas (atomos o moleculas) que interactuan y la fuerza que ejercen mutuamente se puede modelar como la generada por un resorte. Dentro de este contexto el calor se puede entender como la energia que tienen las particulas y que se evidencia como osicilacioens. Si los extremos de un cuerpo estan expuestos a distintas temperaturas las respectivas oscilaciones seran de distinta amplitud:

Conducción
Las particulas que oscilan comienzan via las fuerzas que las ligan a propagar la oscilación y con ello la correspondiente energía y temperatura. Con el tiempo toda la cadena presentara oscilacioens que seran mas intensas en el extremo a una temperatura mayor (por ejemplo la temperatura en la superficie interior ($T_{is}$)) y menor en el otro extremo (por ejemplo la temperatura en la superficie exterior ($T_{es}$)).
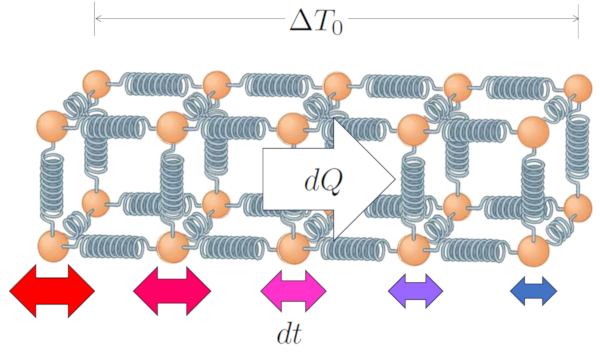
De esta forma la energía, y con ello el calor, se propaga en función de la diferencia de temperatura en el conductor ($\Delta T_0$) que es:
| $ \Delta T_0 = T_{is} - T_{es} $ |
ID:(7718, 0)
