Benützer:
Wärmeleitung
Storyboard 
Der Wärmetransport besteht aus zwei abwechselnden Prozessen. Einerseits gibt es die Wärmeleitung durch ein Medium und andererseits den Wärmeübergang von einem Medium zum anderen.
Der Transport durch ein Medium umfasst die Übertragung der Wärme in das Medium, gefolgt von der Leitung durch dieses und schließlich der Abgabe der Wärme aus dem Medium. In komplexeren Medien müssen mehrere Stufen der Leitung und des Übergangs zwischen verschiedenen Medien berücksichtigt werden. Wenn Wärme in einem der Medien erzeugt oder absorbiert wird, wird die Leitung von oder zu dieser Wärmequelle bzw. -senke berücksichtigt.
ID:(313, 0)
Wärmeleitungsmechanismus
Konzept
Die Wärme, die von einem
und die Leitfähigkeit
ID:(7718, 0)
Geometrie und Materialabhängigkeit
Top
Einer der Schlüsselfaktoren, der bestimmt, wie viel Wärme durch einen Feststoff oder eine Flüssigkeit geleitet werden kann, ist sein Querschnitt, das heißt, die Anzahl der verfügbaren Atomketten. Je mehr dieser Ketten wir haben, desto größer ist unsere Wärmetransportkapazität.
Jedoch kann die Länge dieser Ketten kontraproduktiv sein. Wenn die Federkette länger wird, nimmt unsere Fähigkeit zur Wärmeübertragung ab, da mehr Atome ihre Schwingungsamplituden anpassen müssen.
Wenn wir dies mit die Abschnitt ($S$) und der Leitungslänge ($L$) darstellen, nimmt das Diagramm folgende Form an:
Schließlich erklärt die Fähigkeit des Mediums und des Materials zur Wärmeübertragung, die durch die Koeffizienten der Interner Übertragungskoeffizient ($\alpha_i$) und der Externer Transmissionskoeffizient ($\alpha_e$) und die Wärmeleitfähigkeit ($\lambda$) beschrieben wird, wie die Wärme in Reaktion auf die Temperaturdifferenz ($\Delta T$) übertragen wird, das durch die Differenz zwischen die Innentemperatur ($T_i$) und die Außentemperatur ($T_e$) erzeugt wird:
Dies wird wie folgt berechnet:
| $ \Delta T = T_i - T_e $ |
ID:(15235, 0)
Wärmeleitung
Top
Die Wärmeleitung wurde erstmals von Jean Baptiste Joseph Fourier [1] modelliert, der festlegte, dass die Wärmestromrate ($q$), definiert durch die Wärme transportiert ($dQ$), die Zeitvariation ($dt$) und die Abschnitt ($S$), durch die folgende Gleichung ausgedrückt wird:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
Diese Theorie steht auch in Beziehung zu die Abschnitt ($S$), der Leitungslänge ($L$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Wärmeleitfähigkeit ($\lambda$), wie in der folgenden Gleichung dargestellt:
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
und wird durch das folgende Diagramm veranschaulicht:
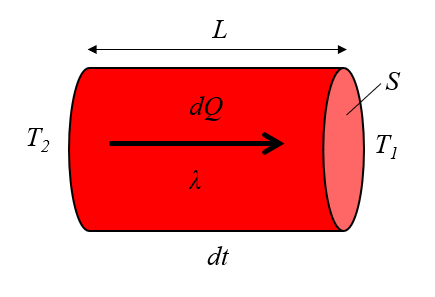
[1] "Théorie Analytique de la Chaleur" (Die analytische Theorie der Wärme), Jean Baptiste Joseph Fourier, 1822.
ID:(15236, 0)
Modell
Top
Berechnungen
Variablen
Parameter
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden Gleichung
$ \Delta T_0 = T_{is} - T_{es} $
DT_0 = T_is - T_es
$ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$
q = dQ /( S * dt )
$ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $
q = lambda * DT_0 / L
$ q =\displaystyle\frac{ \lambda }{ r_e \ln\left(\displaystyle\frac{ r_e }{ r_i }\right)} \Delta T_0 $
q = lambda *ln( r_e / r_i )* DT_0 / r_e
$ S = 2 \pi r_e L $
S = 2* pi * r_e * L
$ T_z = T_{is} + ( T_{es} - T_{is} )\displaystyle\frac{ z }{ L }$
T_z = T_is + ( T_es - T_is )* z / L
$T_r=\displaystyle\frac{\ln\left(\displaystyle\frac{r}{r_i}\right)}{\ln\left(\displaystyle\frac{r_e}{r_i}\right)}(T_{es}-T_{is})+T_{is}$
T(r)=(ln(r/r_i)/ln(r_e/r_i))(T_es-T_is)+T_is
ID:(15334, 0)
Oberflächentemperaturunterschied
Gleichung
Im Fall eines Festkörpers und ähnlich für eine Flüssigkeit können wir das System als eine Struktur von Atomen beschreiben, die durch etwas verbunden sind, das sich wie eine Feder verhält. Wenn beide Enden Temperaturen von eine Temperaturunterschied im Leiter ($\Delta T_0$) haben, wobei die Innenoberflächentemperatur ($T_{is}$) und die Äußere Oberflächentemperatur ($T_{es}$) sind:
| $ \Delta T_0 = T_{is} - T_{es} $ |
ID:(15120, 0)
Wärmefluss
Gleichung
Der die Wärmestromrate ($q$) wird basierend auf die Wärme transportiert ($dQ$) definiert, der die Abschnitt ($S$) in die Zeitvariation ($dt$) durchläuft:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
ID:(3482, 0)
Temperaturverteilung
Gleichung
Die Temperatur im Radius r ($T_r$) ist eine Funktion von der Radio ($r$), die mit der Innenradius ($r_i$), die Innenoberflächentemperatur ($T_{is}$), der Outdoor-Radio ($r_e$) und < var>5214 ist:
| $ T_z = T_{is} + ( T_{es} - T_{is} )\displaystyle\frac{ z }{ L }$ |
ID:(15747, 0)
Berechnung der Wärmeleitung
Gleichung
Der Wärmefluss ($q$) ist eine Funktion von die Wärmeleitfähigkeit ($\lambda$), der Leitungslänge ($L$) und die Temperaturunterschied im Leiter ($\Delta T_0$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
ID:(7712, 0)
Radiale Temperaturverteilung im Rohr
Gleichung
Die Temperatur im Radius r ($T_r$) ist eine Funktion von der Radio ($r$), die mit der Innenradius ($r_i$), die Innenoberflächentemperatur ($T_{is}$), der Outdoor-Radio ($r_e$) und < var>5214 ist:
| $T_r=\displaystyle\frac{\ln\left(\displaystyle\frac{r}{r_i}\right)}{\ln\left(\displaystyle\frac{r_e}{r_i}\right)}(T_{es}-T_{is})+T_{is}$ |
Die zeitliche Veränderung des Wärmeflusses $\dot{Q}$ in Polarkoordinaten, wobei $r$ den Radius darstellt und die Wärmeleitfähigkeit ($\lambda$) ist:
$\dot{Q}=-\lambda\displaystyle\frac{1}{r}\displaystyle\frac{\partial}{\partial r}\left(r\displaystyle\frac{\partial T}{\partial r}\right)$
Wenn der Fluss stationär ist, ist seine zeitliche Ableitung null und die Gleichung reduziert sich auf null. Die Lösung dieser Gleichung, gegeben die Randbedingungen, bei denen die Temperaturen bei der Innenradius ($r_i$) Die Innenoberflächentemperatur ($T_{is}$) und bei der Outdoor-Radio ($r_e$) Die Äußere Oberflächentemperatur ($T_{es}$) sind, wird beschrieben als:
| $T_r=\displaystyle\frac{\ln\left(\displaystyle\frac{r}{r_i}\right)}{\ln\left(\displaystyle\frac{r_e}{r_i}\right)}(T_{es}-T_{is})+T_{is}$ |
ID:(7741, 0)
Wärmestrom im Rohr
Gleichung
Die Wärmestromrate ($q$) ist mit die Temperaturunterschied im Leiter ($\Delta T_0$), die Wärmeleitfähigkeit ($\lambda$), der Innenradius ($r_i$) und der Outdoor-Radio ($r_e$) ist:
| $ q =\displaystyle\frac{ \lambda }{ r_e \ln\left(\displaystyle\frac{ r_e }{ r_i }\right)} \Delta T_0 $ |
ID:(7742, 0)
Rohroberfläche
Gleichung
Die Abschnitt ($S$) ist eine Funktion von der Leitungslänge ($L$) und der Outdoor-Radio ($r_e$) ist:
| $ S = 2 \pi r_e L $ |
ID:(15748, 0)