Benützer:
Wärmeübergang
Storyboard 
Wärme wird innerhalb eines Mediums bis zur Grenzfläche mit einem anderen Medium geleitet. Zwischen beiden Medien erfolgt der Wärmetransfer in Abhängigkeit von der Temperaturdifferenz zwischen den Medien, der Kontaktfläche und einer Wärmeübertragungskonstanten. Wenn eines der Medien ein Gas (z.B. Luft) oder eine Flüssigkeit (z.B. Wasser) ist, hängt die Wärmeübertragungskonstante von der Struktur der Grenzfläche und der Strömungsgeschwindigkeit des gasförmigen oder flüssigen Mediums ab.
ID:(776, 0)
Abhängigkeit der Wärmeübertragung von der Geometrie zum Leiter
Top
Der Haupttreiber für den Wärmeübergang von einem Medium auf einen Leiter ist der Temperaturunterschied. In dem Medium die Innentemperatur ($T_i$) haben die Teilchen mehr Energie, und wenn sie mit denen im Leiter bei eine Innenoberflächentemperatur ($T_{is}$) kollidieren, neigen sie dazu, die Energie des Letzteren zu erhöhen. Diese Interaktion kann wie folgt dargestellt werden:
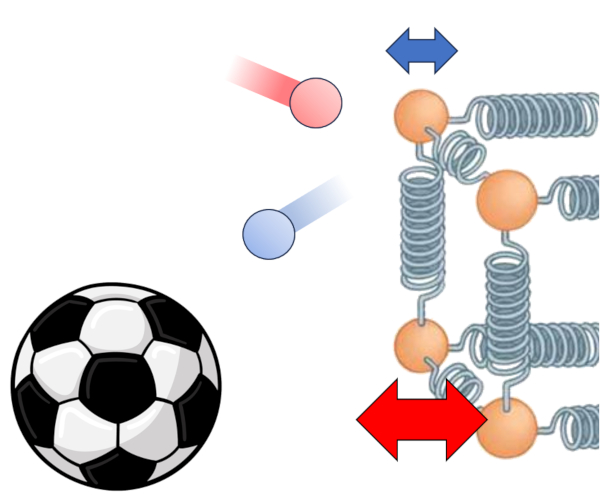
Neben der Temperatur selbst hängt der Wärmefluss von die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) ab:
| $ \Delta T_i = T_i - T_{is} $ |
Ein weiterer entscheidender Faktor ist die Anzahl der Atome, deren Oszillationsamplitude erhöht werden kann, was von die Abschnitt ($S$) abhängt. Schließlich müssen wir auch die Eigenschaften der Oberfläche berücksichtigen, die durch der Interner Übertragungskoeffizient ($\alpha_i$) beschrieben werden. Dies entspricht dem Verhältnis zwischen übertragener Wärme, Oberfläche, Temperaturunterschied und verstrichener Zeit:
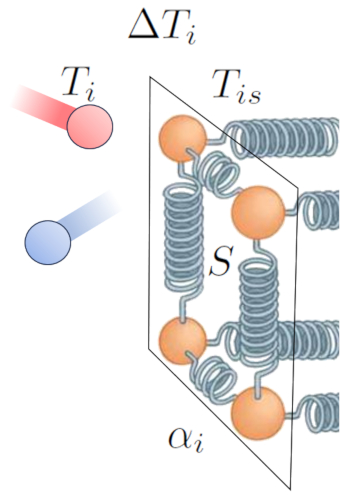
ID:(15237, 0)
Berechnung der Wärmeübertragung auf den Leiter
Top
Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Wärmestromrate ($q$) basierend auf die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$) zu berechnen:
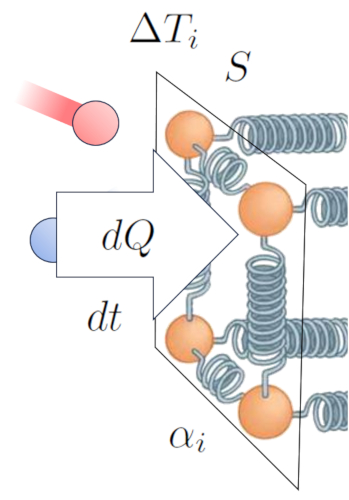
Dies kann mathematisch wie folgt ausgedrückt werden:
| $ q = \alpha_i \Delta T_i $ |
ID:(15238, 0)
Abhängigkeit der Wärmeübertragung von der Geometrie des Leiters
Top
Der Haupttreiber für den Wärmeübergang von einem Leiter zu einem Medium ist der Temperaturunterschied. Wenn die Äußere Oberflächentemperatur ($T_{es}$), haben die Teilchen mehr Energie und schwingen mit einer größeren Amplitude, wenn sie mit den Atomen und Molekülen des Mediums bei eine Außentemperatur ($T_e$) interagieren. Dies führt dazu, dass die Energie dieser letzten erhöht wird. Diese Interaktion kann wie folgt dargestellt werden:
Neben der Temperatur hängt der Wärmefluss von die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) ab.
| $ \Delta T_e = T_{es} - T_e $ |
Ein weiterer entscheidender Faktor ist die Anzahl der Atome, deren Oszillationsamplitude erhöht werden kann, was von die Abschnitt ($S$) abhängt. Abschließend müssen wir die Oberflächeneigenschaften berücksichtigen, die durch der Externer Transmissionskoeffizient ($\alpha_e$) repräsentiert werden. Dies entspricht dem Verhältnis zwischen übertragener Wärme, Oberfläche, Temperaturunterschied und verstrichener Zeit:
ID:(15239, 0)
Wärmeübertragung vom Leiter
Top
Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Wärmestromrate ($q$) basierend auf die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und der Externer Transmissionskoeffizient ($\alpha_e$) zu berechnen:
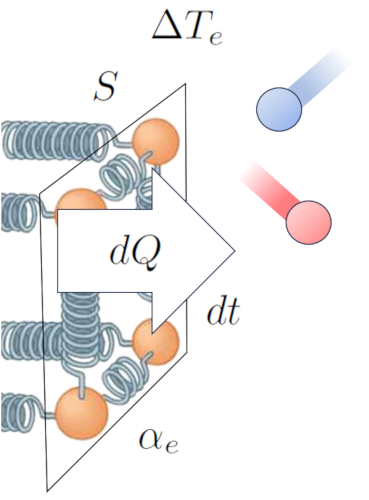
Dies kann mathematisch wie folgt ausgedrückt werden:
| $ q = \alpha_e \Delta T_e $ |
ID:(15240, 0)
Wärmeübertragung zum und vom Leiter
Konzept
Die erste Beschreibung des Wärmeübertragungsmodells an der Schnittstelle zwischen zwei Medien wurde von Thomas Graham Balfour [1] entwickelt. Seine Theorie geht davon aus, dass die übertragene Wärmemenge von der Temperaturdifferenz und einer spezifischen Konstanten der Schnittstelle abhängt.
Wenn die Wärme an den Leiter, dargestellt durch die Wärmestromrate ($q$) zusammen mit der Interner Übertragungskoeffizient ($\alpha_i$) und die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), übertragen wird, wird dies durch die folgende Gleichung ausgedrückt:
| $ q = \alpha_i \Delta T_i $ |
Im Fall, dass die Wärme vom Leiter, repräsentiert durch die Wärmestromrate ($q$) zusammen mit der Externer Transmissionskoeffizient ($\alpha_e$) und die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$), übergeht, wird dies durch die folgende Gleichung spezifiziert:
| $ q = \alpha_e \Delta T_e $ |
[1] "The Theory of Heat" (Die Theorie der Wärme), Thomas Graham Balfour, 1876.
ID:(15123, 0)
Wärmetransport
Konzept
Das grundlegende System umfasst eine Übertragung, die durch die Temperaturdifferenz ($\Delta T$) generiert wird und aus die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$), die Temperaturunterschied im Leiter ($\Delta T_0$) und die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) besteht. Daher:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Mit die Wärmestromrate ($q$) als Verantwortlichem für die Übertragung zwischen dem Inneren und dem Leiter, verwendet der Interner Übertragungskoeffizient ($\alpha_i$):
| $ q = \alpha_i \Delta T_i $ |
Die Leitung betrifft die Wärmeleitfähigkeit ($\lambda$) und der Leitungslänge ($L$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Und der Transfer vom Leiter nach außen, mit der Externer Transmissionskoeffizient ($\alpha_e$), wird dargestellt durch:
| $ q = \alpha_e \Delta T_e $ |
All dies wird grafisch dargestellt durch:
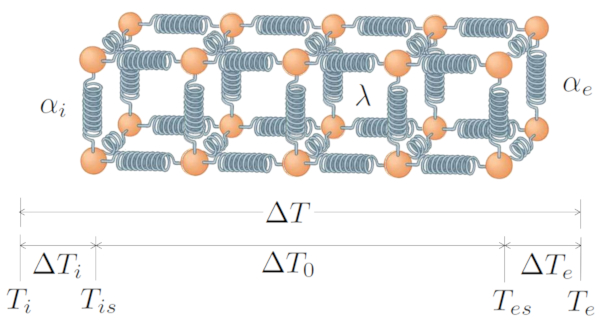
ID:(7723, 0)
Abhängigkeit des Übertragungskoeffizienten von der Geschwindigkeit des Mediums
Konzept
Einer der Effekte der Wärmeübertragung von einem Leiter auf ein externes Medium ist die Erwärmung des Mediums nahe der Schnittstelle, was eine Interferenzzone in der Übertragung schafft. Dies verringert die Effizienz der Übertragung und führt dazu, dass eine isolierende Schicht entsteht, die den Energiefluss reduziert.
Dieser Effekt kann sich jedoch in Anwesenheit von Wind ändern. Der Wind kann die Schicht aus hochtemperierten Atomen und Molekülen entfernen, wodurch die Effizienz der Wärmeübertragung verbessert wird. Dies deutet darauf hin, dass der Durchgangskoeffizient ($\alpha$) von die Mittlere Geschwindigkeit ($v_m$) beeinflusst wird [1,2]:
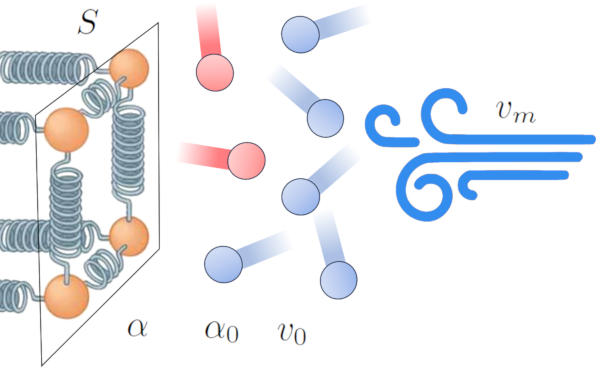
In diesem Zusammenhang modellieren wir die Beziehung basierend auf Übertragungskoeffizient ohne Geschwindigkeit ($\alpha_0$) und einem Referenzfaktor von der Medienreferenzgeschwindigkeit ($v_0$).
Die mathematische Beziehung, die dieses Phänomen für ein Gas mit der Transmissionskoeffizient in Gasen, abhängig von der Geschwindigkeit ($\alpha_{gv}$), die Mittlere Geschwindigkeit ($v_m$), der Transmissionskoeffizient in Gasen, unabhängig von der Geschwindigkeit ($\alpha_{g0}$) und der Transmissionskoeffizient Gasgeschwindigkeitsfaktor ($v_{g0}$) beschreibt, ist:
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
Und für eine Flüssigkeit mit der Durchgangskoeffizient abhängig von der Geschwindigkeit ($\alpha_{wv}$), die Mittlere Geschwindigkeit ($v_m$), der Durchgangskoeffizient unabhängig von der Geschwindigkeit ($\alpha_{w0}$) und der Factor Velocidad del Coefiente de Transmisión ($v_{w0}$):
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
Dies zeigt, wie der Wind die Effizienz der Wärmeübertragung zwischen einem Leiter und einem externen Medium erheblich beeinflussen kann.
[1] "Über Flüssigkeitsbewegung bei sehr kleiner Reibung", Ludwig Prandtl, 1904
[2] "Die Abhängigkeit der Wärmeübergangszahl von der Rohrlänge", Wilhelm Nusselt, 1910
ID:(3620, 0)
Modell
Top
Berechnungen
Variablen
Parameter
zu 
, dann die Variable auswählen: 
zu 
Berechnungen
Berechnungen
Variable 
Gegeben Berechnen 
Ziel : Gleichung Zu verwenden Gleichung
$ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$
alpha_gv = alpha_g0 * (1+ v_m / v_g0 )
$ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$
alpha_wv = alpha_w0 * (1+sqrt( v_m / v_w0 ))
$ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $
DT = DT_i + DT_0 + DT_e
$ \Delta T_0 = T_{is} - T_{es} $
DT_0 = T_is - T_es
$ \Delta T_e = T_{es} - T_e $
DT_e = T_es - T_e
$ \Delta T_i = T_i - T_{is} $
DT_i = T_i - T_is
$ q = \alpha_e \Delta T_e $
q = alpha_e * DT_e
$ q = \alpha_i \Delta T_i $
q = alpha_i * DT_i
$ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$
q = dQ /( S * dt )
$ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $
q = lambda * DT_0 / L
ID:(15335, 0)
Temperaturunterschied zwischen Medium und Leiter
Gleichung
Die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) wird berechnet, indem die Innenoberflächentemperatur ($T_{is}$) von die Innentemperatur ($T_i$) subtrahiert wird:
| $ \Delta T_i = T_i - T_{is} $ |
ID:(15117, 0)
Temperaturdifferenz Leiter zu Medium
Gleichung
Die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) wird berechnet, indem die Äußere Oberflächentemperatur ($T_{es}$) von die Außentemperatur ($T_e$) subtrahiert wird:
| $ \Delta T_e = T_{es} - T_e $ |
ID:(15118, 0)
Oberflächentemperaturunterschied
Gleichung
Im Fall eines Festkörpers und ähnlich für eine Flüssigkeit können wir das System als eine Struktur von Atomen beschreiben, die durch etwas verbunden sind, das sich wie eine Feder verhält. Wenn beide Enden Temperaturen von eine Temperaturunterschied im Leiter ($\Delta T_0$) haben, wobei die Innenoberflächentemperatur ($T_{is}$) und die Äußere Oberflächentemperatur ($T_{es}$) sind:
| $ \Delta T_0 = T_{is} - T_{es} $ |
ID:(15120, 0)
Gesamttemperaturschwankung
Gleichung
Im Prozess des Wärmetransports sinkt die Temperatur allmählich vom System mit der höchsten Temperatur (intern) zum System mit der niedrigsten Temperatur (extern). In diesem Prozess nimmt sie zuerst von der durchschnittlichen internen Temperatur auf die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) ab, dann auf die Temperaturunterschied im Leiter ($\Delta T_0$) und schließlich auf die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$). Die Summe dieser drei Veränderungen entspricht dem Gesamtabfall, nämlich die Temperaturdifferenz ($\Delta T$), wie unten gezeigt:
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
ID:(15115, 0)
Wärmefluss
Gleichung
Der die Wärmestromrate ($q$) wird basierend auf die Wärme transportiert ($dQ$) definiert, der die Abschnitt ($S$) in die Zeitvariation ($dt$) durchläuft:
| $ q \equiv \displaystyle\frac{1}{ S }\displaystyle\frac{ dQ }{ dt }$ |
ID:(3482, 0)
Berechnung der Wärmeübertragung auf den Leiter
Gleichung
Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Wärmestromrate ($q$) basierend auf die Temperaturunterschied an der internen Schnittstelle ($\Delta T_i$) und der Interner Übertragungskoeffizient ($\alpha_i$) zu berechnen:
| $ q = \alpha_i \Delta T_i $ |
ID:(15113, 0)
Berechnung der Wärmeübertragung vom Leiter
Gleichung
Auf diese Weise etablieren wir eine Beziehung, die es uns ermöglicht, die Wärmestromrate ($q$) basierend auf die Temperaturunterschied an der externen Schnittstelle ($\Delta T_e$) und der Externer Transmissionskoeffizient ($\alpha_e$) zu berechnen:
| $ q = \alpha_e \Delta T_e $ |
ID:(15114, 0)
Berechnung der Wärmeleitung
Gleichung
Der Wärmefluss ($q$) ist eine Funktion von die Wärmeleitfähigkeit ($\lambda$), der Leitungslänge ($L$) und die Temperaturunterschied im Leiter ($\Delta T_0$):
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
ID:(7712, 0)
Konstante Wärmeübertragung in Flüssigkeit
Gleichung
Wenn ein Medium mit einer Konstanten von der Durchgangskoeffizient abhängig von der Geschwindigkeit ($\alpha_{wv}$) bewegt wird und die Mittlere Geschwindigkeit ($v_m$) gleich
| $ \alpha_{wv} = \alpha_{w0} \left(1+\sqrt{\displaystyle\frac{ v_m }{ v_{w0} }}\right)$ |
ist, wobei der Durchgangskoeffizient unabhängig von der Geschwindigkeit ($\alpha_{w0}$) den Fall repräsentiert, in dem sich das Medium nicht bewegt, und der Factor Velocidad del Coefiente de Transmisión ($v_{w0}$) die Referenzgeschwindigkeit ist.
Die thermische Übertragungskonstante des Materials für den Fall einer ruhenden Flüssigkeit beträgt $340 J/m^2sK$, während die Referenzgeschwindigkeit $0,0278 m/s$ beträgt.
ID:(7714, 0)
Konstante Wärmeübertragung in Gas
Gleichung
Falls ein Medium sich mit einer Konstanten von eine Mittlere Geschwindigkeit ($v_m$) bewegt und der Transmissionskoeffizient in Gasen, abhängig von der Geschwindigkeit ($\alpha_{gv}$) gleich ist
| $ \alpha_{gv} = \alpha_{g0} \left(1+\displaystyle\frac{ v_m }{ v_{g0} }\right)$ |
wobei der Transmissionskoeffizient in Gasen, unabhängig von der Geschwindigkeit ($\alpha_{g0}$) den Fall repräsentiert, in dem das Medium sich nicht bewegt, und der Transmissionskoeffizient Gasgeschwindigkeitsfaktor ($v_{g0}$) die Referenzgeschwindigkeit ist.
Die thermische Transferkonstante für das Material im Fall eines ruhenden Gases beträgt $5,6 J/m^2sK$, während die Referenzgeschwindigkeit $1,41 m/s$ beträgt.
ID:(7715, 0)