Transport de chaleur
Storyboard 
Le transport de chaleur à travers un système composé de plusieurs milieux peut être estimé en analysant comment la chaleur est conduite dans chaque milieu et transférée à chaque interface. Le calcul est effectué en utilisant les paramètres spécifiques de chaque milieu et interface, ainsi que les températures aux deux extrémités du système, fournissant ainsi les températures à chaque interface.
ID:(1483, 0)
Transport de chaleur
Image 
Le système de base comprend un transfert généré par a différence de température ($\Delta T$), qui se compose de a différence de température à l'interface interne ($\Delta T_i$), a différence de température dans le conducteur ($\Delta T_0$) et a différence de température à l'interface externe ($\Delta T_e$). Par conséquent :
| $ \Delta T = \Delta T_i + \Delta T_0 + \Delta T_e $ |
Avec a débit de chaleur ($q$) responsable du transfert entre l'intérieur et le conducteur, utilisant le coefficient de transmission interne ($\alpha_i$) :
| $ q = \alpha_i \Delta T_i $ |
La conduction implique a conductivité thermique ($\lambda$) et le longueur du pilote ($L$) :
| $ q = \displaystyle\frac{ \lambda }{ L } \Delta T_0 $ |
Et le transfert du conducteur vers l'extérieur, avec le coefficient de transmission externe ($\alpha_e$), est représenté par :
| $ q = \alpha_e \Delta T_e $ |
Tout cela est représenté graphiquement par :
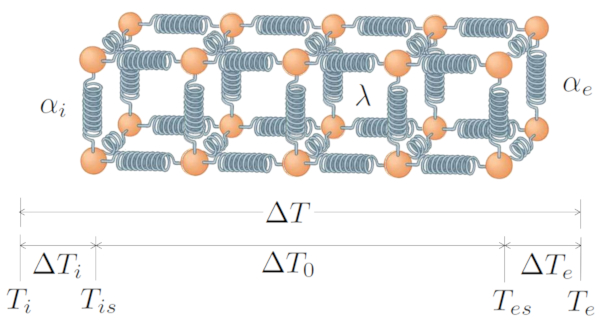
ID:(7723, 0)
Transport de chaleur entre deux systèmes via un troisième fluide
Noter 
A débit de chaleur ($q$) est calculé à partir de le coefficient de transport total (supports multiples, deux interfaces) ($k$) et a différence de température ($\Delta T$) en utilisant l'équation suivante :
| $ q = k \Delta T $ |
où Le coefficient de transport total (supports multiples, deux interfaces) ($k$) est dérivé de le coefficient de transmission externe ($\alpha_e$), le coefficient de transmission interne ($\alpha_i$), a conductivité thermique ($\lambda$) et le longueur du pilote ($L$) grâce à cette équation :
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\displaystyle\frac{ L }{ \lambda }$ |
Ceci est représenté dans l'image ci-dessous :
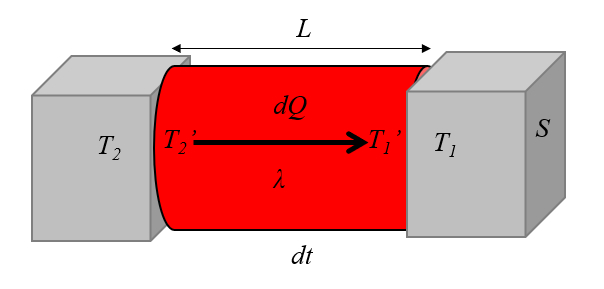
ID:(1675, 0)
Profil de température
Citation 
Généralement, la variation de la température à l'intérieur d'un conducteur suit une tendance linéaire. Cependant, dans le cas de milieux gazeux et/ou liquides en contact avec le conducteur, il y a une variation progressive de la température du centre du milieu à la surface, comme représenté dans l'image suivante :

a température de la surface extérieure ($T_{es}$) dépend de a température extérieure ($T_e$), le coefficient de transport total ($k$), le coefficient de transmission externe ($\alpha_e$) et a différence de température ($\Delta T$):
| $ T_{es} = T_e + \displaystyle\frac{ k }{ \alpha_e } \Delta T $ |
a température de la surface intérieure ($T_{is}$) est une fonction de a température intérieure ($T_i$) et le coefficient de transmission interne ($\alpha_i$):
| $ T_{is} = T_i - \displaystyle\frac{ k }{ \alpha_i } \Delta T $ |
et a différence de température ($\Delta T$):
| $ \Delta T = T_i - T_e $ |
ID:(7722, 0)
Transport du flux de chaleur total
Exercer 
Lorsque le matériel comprend plusieurs conducteurs connectés en série, le coefficient de transport total (supports multiples, deux interfaces) ($k$) est calculé à partir de le coefficient de transmission externe ($\alpha_e$), le coefficient de transmission interne ($\alpha_i$), a élément de conductivité thermique i ($\lambda_i$) et le longueur de l'élément i ($L_i$) en utilisant l'équation :
| $\displaystyle\frac{1}{ k }=\displaystyle\frac{1}{ \alpha_i }+\displaystyle\frac{1}{ \alpha_e }+\sum_i\displaystyle\frac{ L_i }{ \lambda_i }$ |
Ce processus est illustré dans le diagramme suivant :

ID:(7721, 0)
