Aplicación en Microscopios
Storyboard 
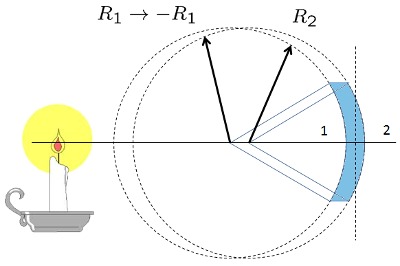
El principio del microscopio es capturar la imagen pequeña, que arriba como haces paralelos y agrandarla con un lente biconvexo para formar una imagen real invertida de mayor tamaño.
ID:(299, 0)
Geometría de los haces en un lente, objeto cercano
Imagen 
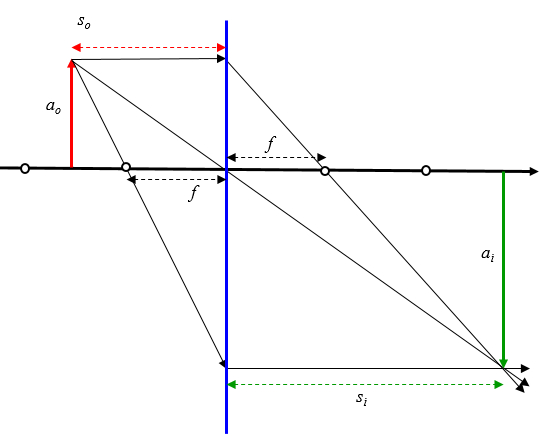
En el caso de que el objeto esta mas cercano al lente que el punto focal el diagrama para determinar tamaño y posición de la imagen es algo mas complejo. En este caso los haces deben ser
-- proyectados desde donde habrían llegado al objeto que los irradia
-- dentro de la proyección se deben seguir las mismas reglas que en un haz real
En este caso basta nuevamente diagramar los mismos tres haces:
- en forma paralela al eje óptico se refracta por el foco
- vía el foco se refracta en forma paralela al eje óptico
- vía el origen del eje óptico continua en forma rectilínea
y se obtiene de la misma forma la imagen:
ID:(9783, 0)
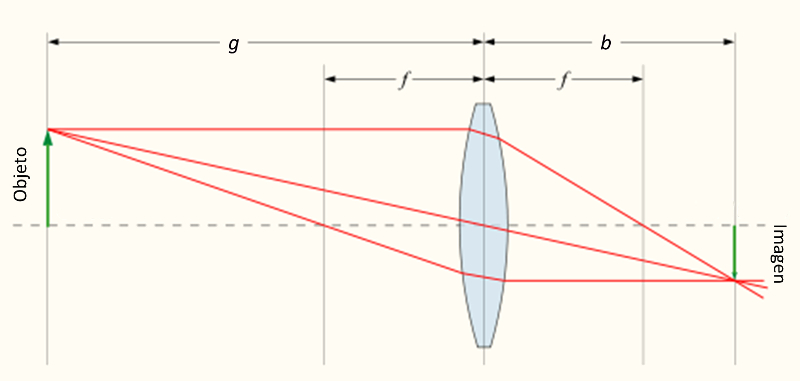
Geometría de los haces en un lente biconvexo
Imagen 
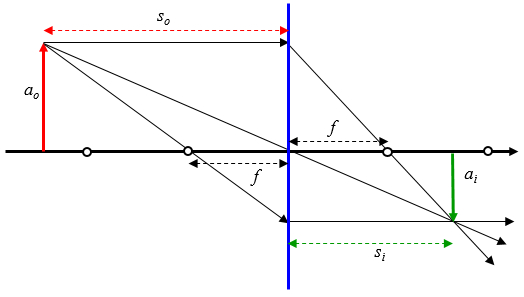
En el caso de un lente biconvexo un haz que alcanza el lente
- en forma paralela al eje óptico se refracta por el foco
- vía el foco se refracta en forma paralela al eje óptico
- vía el origen del eje óptico continua en forma rectilínea
lo que para el caso de un objeto a una distancia mayor que el foto corresponde a:
ID:(1856, 0)
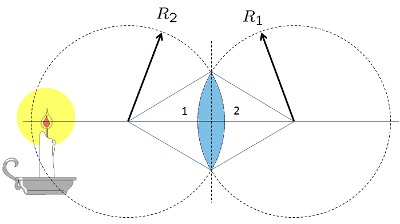
Lente convexo
Imagen 
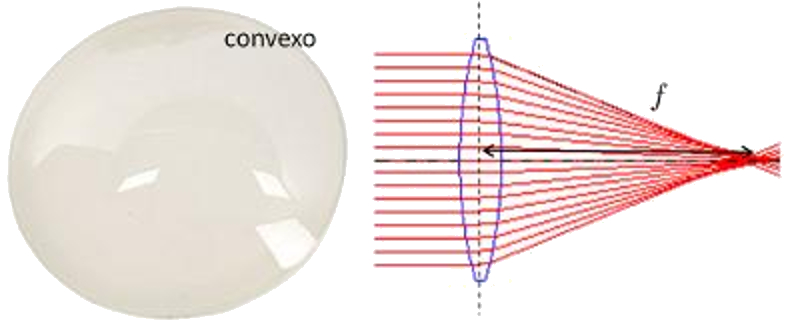
Un lente convexo es un lente que refracta el el haz de luz paralelo que incide en forma paralela a través del foco de este:
ID:(1855, 0)
Posición y foco de lentes concavos
Ecuación 
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}
Con la relación de similitud de los triángulos
| \displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} } |
se puede mostrar que se cumple:
| \displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} } |
ID:(3347, 0)
Proporciones de tamaño y posición de lentes concavos
Ecuación 
Para cualquier lente se puede dibujar haces característicos con los cuales se puede por similitud mostrar que los tamaños del objeto y la imagen están en la misma proporción que sus distancias hasta el elemento óptico (lente o espejo).
Si el objeto tiene un tamaño
ID:(3346, 0)
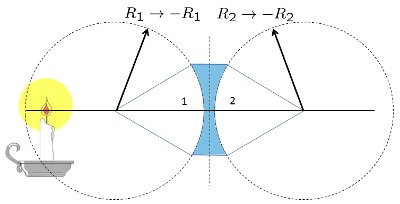
Lente Cóncavo
Imagen 
Los lentes convexos son mas delgados en su centro ensanchándose hacia los bordes.
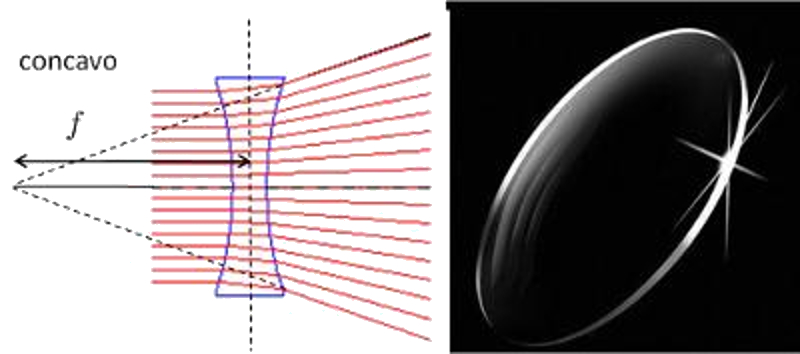
Los haces de luz que inciden en forma paralela son dispersados como si la luz se emitiera en el foco del lente.
ID:(1854, 0)
Cálculo del fóco de un lente bi-convexo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3432, 0)
Cálculo del foco de un lente bi-convexo grueso
Ecuación 
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene un indice de refracción
ID:(3348, 0)
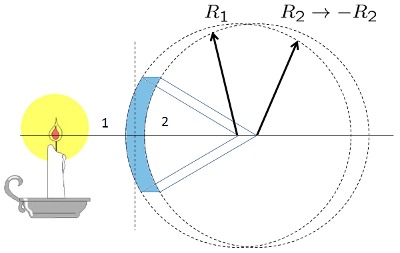
Cálculo del foco de un lente convexo-concavo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3430, 0)
Cálculo del foco de un lente convexo-cóncavo grueso
Ecuación 
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
ID:(3350, 0)
Cálculo del fóco de un lente bi-concavo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3431, 0)
Cálculo del foco de un lente concavo-convexo grueso simétrico
Ecuación 
Una caso especial es aquel en que los radios son iguales, o sea
ID:(3429, 0)
Cálculo del foco de un lente bi-cóncavo grueso
Ecuación 
Los lentes reales tienen un grosor que se debe considerar. Si el lente tiene vidrio con indice de refracción
ID:(3349, 0)
Multiples lentes
Imagen 
Cuando se acoplan dos lentes con sus respectivos focos, el primer lente genera una imagen que funciona como objeto para el segundo lente que a su vez genera una imagen de una imagen:
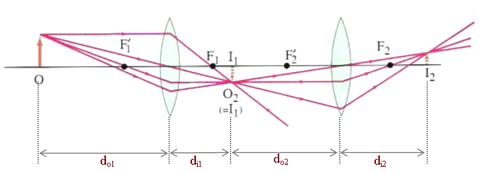
ID:(9465, 0)
Refracción según el color de la luz
Imagen 
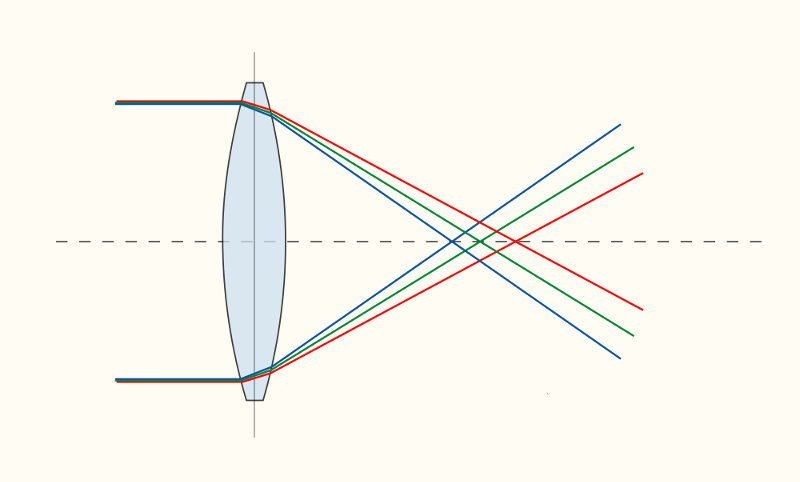
El índice de refracción del vidrio puede depender de la longitud de onda o frecuencia de la luz. En tal caso, se dice que el vidrio es 'cromático'. Si no presenta esta propiedad, se le llama 'acrómico'.
El principal problema de esta propiedad es que la posición del foco de una lente depende del color de la luz. Por lo tanto, una lente óptica tiene el problema de que si el ojo puede enfocar un color, no podrá hacerlo simultáneamente para objetos de otros colores.
ID:(1626, 0)