Usuario:
Lentes Cóncavos
Storyboard 
Los lentes cóncavos divergen el haz incidente siendo emitidos los haces como si procedieran de un punto focal en el lado en que incide el haz.
ID:(1267, 0)
Lente Cóncavo
Imagen
Los lentes convexos son mas delgados en su centro ensanchándose hacia los bordes.
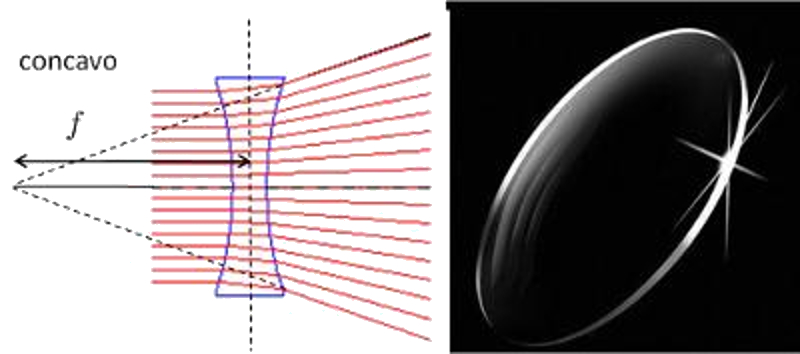
Los haces de luz que inciden en forma paralela son dispersados como si la luz se emitiera en el foco del lente.
ID:(1854, 0)
Calculo de imagen para un lente concavo
Imagen
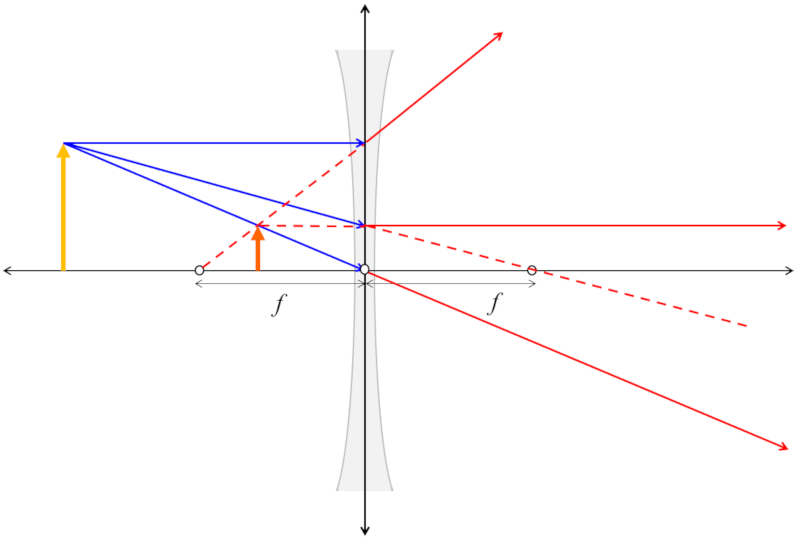
Para poder calcular el tamaño y el lugar en que se presentara la imagen se puede dibujar el eje óptico, el lente concavo y un objeto en una posición y de un tamaño. Sobre este esquema se pueden dibujar tres haces:
• Un haz paralelo al eje óptico que tras incidir sobre el lente continua a lo largo de una linea que sale del foco del mismo lado que el objeto
• Un haz que pasa por el centro del lento continua en una linea recta al otro lado del lente.
• Un haz que pasaría por el foco al otro lado del lente pero que dibuja paralelo al eje óptico
Si se dibuja correctamente los tres haces se cruzaran en un punto. Dicho punto corresponde a la imagen que se crea ya que todos los haces emanan de esta. Del punto se tiene la posición, el tamaño de la imagen y si esta invertida o no.
ID:(12693, 0)
Similitud tamaños y posiciones
Imagen
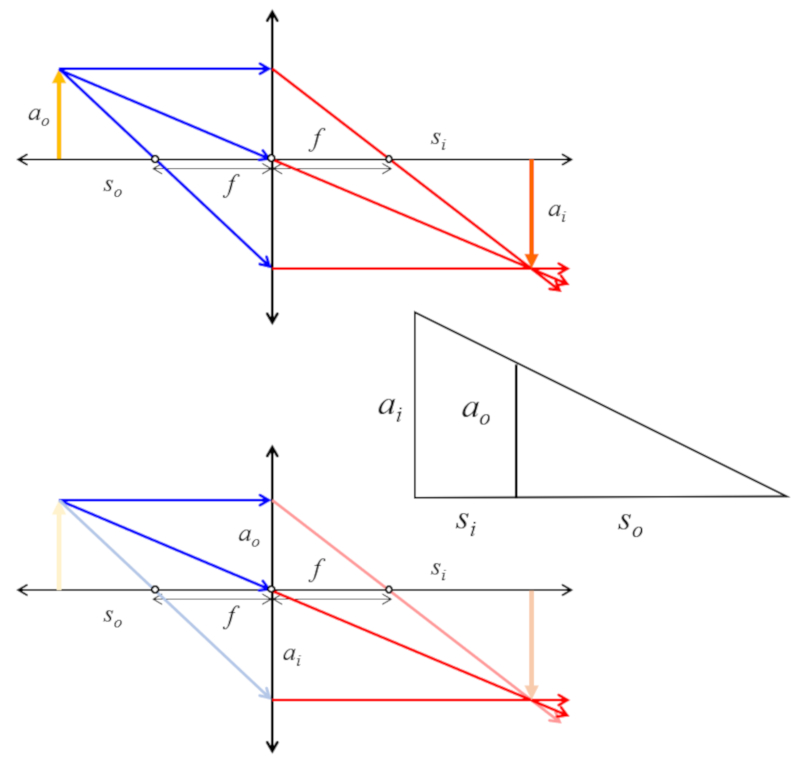
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños con posiciones
ID:(12697, 0)
Similitud tamaños, posición de objeto y foco
Imagen
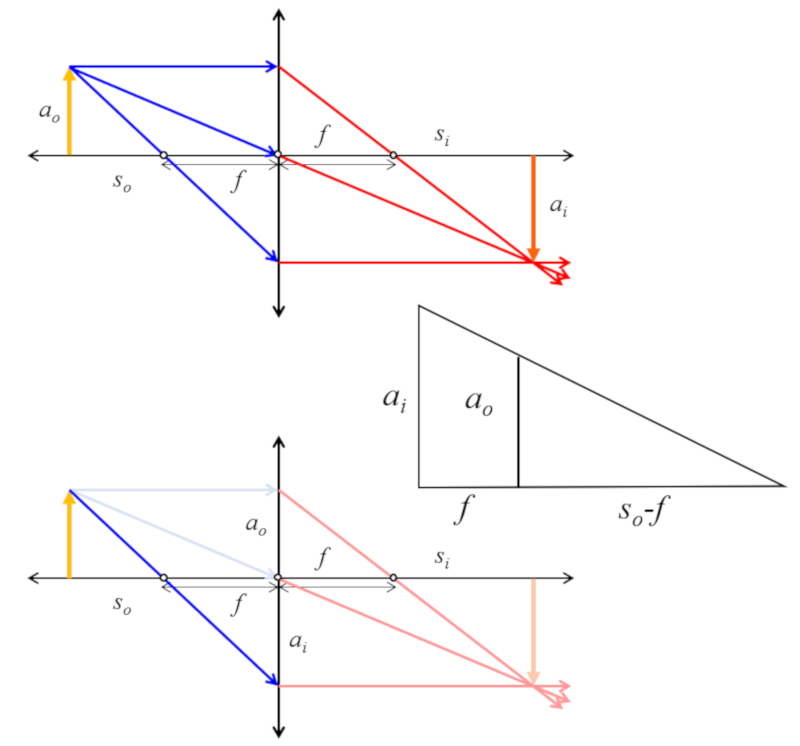
Si se consideran los triángulos del objeto e imagen se tiene que existe una similitud que se puede usar para obtener una relación de tamaños, posición del objeto y foco:
ID:(12698, 0)
Lente concavo con objeto entre origen y foco
Imagen
Si se asume que el objeto esta entre el origen del eje óptico y el foco se tiene:
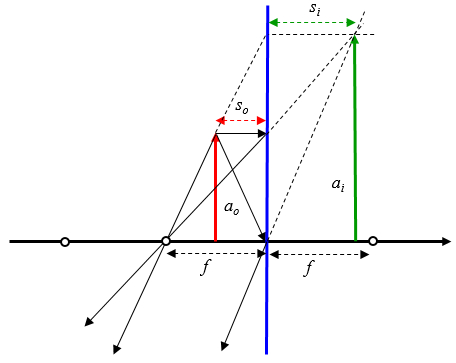
ID:(12690, 0)
Lente concavo con objeto entre el foco y el doble del foco
Imagen
Si se asume que el objeto esta entre el origen del foco y el doble del foco se tiene:
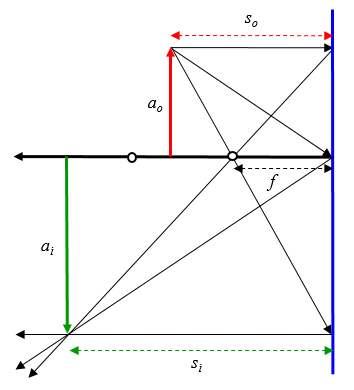
ID:(12691, 0)
Lente concavo con objeto mas lejos que el doble del foco
Imagen
Si se asume que el objeto esta entre el origen esta mas lejos que el doble del foco se tiene:
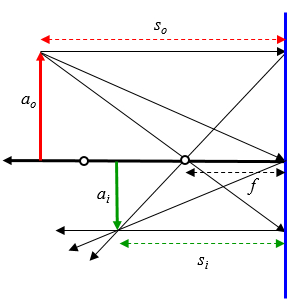
ID:(12692, 0)
Simulación de un lente cóncavo
Descripción
La forma como opera el lente se puede simular con
ID:(14046, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
$\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$
a_o / a_lc = s_o / s_lc
$\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$
1/ f_lc =1/ s_o +1/ s_lc
ID:(16062, 0)
Proporciones de tamaño y posición de lentes concavos
Ecuación
Para cualquier lente se puede dibujar haces característicos con los cuales se puede por similitud mostrar que los tamaños del objeto y la imagen están en la misma proporción que sus distancias hasta el elemento óptico (lente o espejo).
Si el objeto tiene un tamaño
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
ID:(3346, 0)
Posición y foco de lentes concavos
Ecuación
Por similitud de los triángulos de los tamaños del objeto y la imagen y las posiciones del objeto y foco permite por similitud de triángulos mostrar que:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
Una relación se puede armar con los triángulos del lado del objeto. En este caso la similitud nos permite escribir que el tamaño del objeto
$\displaystyle\frac{a_o}{s_o-f}=\displaystyle\frac{a_i}{f}$
Con la relación de similitud de los triángulos
| $\displaystyle\frac{ a_o }{ a_{lc} }=\displaystyle\frac{ s_o }{ s_{lc} }$ |
se puede mostrar que se cumple:
| $\displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} }$ |
ID:(3347, 0)