Usuario: 
Necesidad de lentes
Imagen 
Uno puede solo enfocar un plano a la vez. Para hacerlo nuestro ojo deforma el foco del cristalino estirando o dejando que se contraiga.
Necesitamos un lente óptico cuando no somos capaces de adaptar nuestro cristalino en todo el rango que necesitamos enfocar:
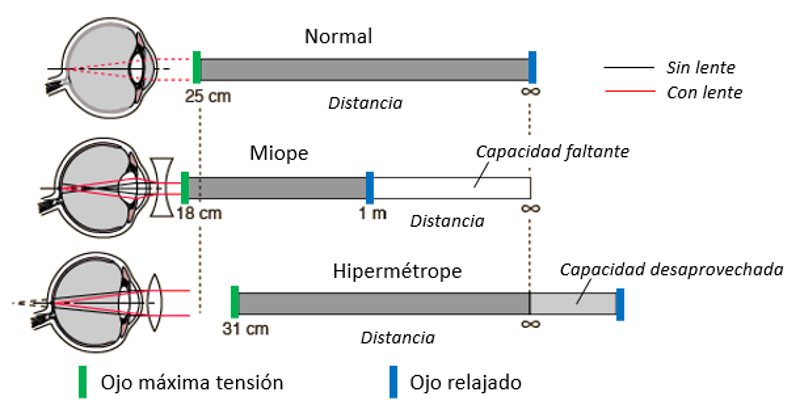
ID:(12749, 0)
Forma como opera el lente óptico
Imagen
Si colocamos un lente frente a nuestros ojos podemos modificar el punto en que proyectamos la imagen. Si antes la imagen se creaba frente o detrás de la retina ahora podemos llevarla sobre la retina:
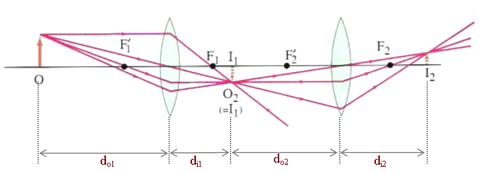
ID:(12750, 0)
Diseño del lente óptico
Imagen
Un anteojo 'contiene' al lente óptico. El vidrio que observamos es solo montaje trasparente:
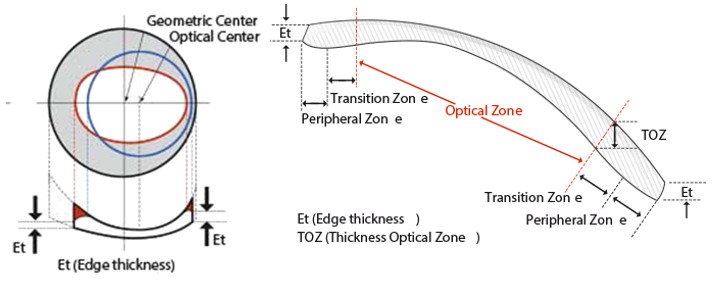
ID:(12751, 0)
Necesidad de localizarlo frente a las pupilas
Imagen
Un anteojo 'contiene' al lente óptico. El vidrio que observamos es solo montaje trasparente:
ID:(12752, 0)
Necesita estar a una distancia dada
Imagen
El lente esta diseñado para trabajar en forma optima a un distancia dada del cristalino:
ID:(12753, 0)
Necesita de estar centrado
Imagen
El lente tiene que estar alineado con el eje óptico del cristalino
ID:(12754, 0)
Modelo
Top
Parámetros
Variables
Cálculos
a 
, luego, seleccione la variable: 
a 
Cálculos
Cálculos
Variable 
Dado Calcule 
Objetivo : Ecuación A utilizar 
Ecuaciones
\displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b }
1/ f_c =1/( D - s_i ) + 1/ s_b
\displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i }
1/ f_lv =1/ s_o + 1/ s_i
\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c }
1/ s_o + 1/( D -1/(1/ f_lv -1/ s_b ))=1/ f_c
ID:(16065, 0)
Ecuación del foco para el lentes opticos
Ecuación
Si observamos la sección objeto - lente óptico - imagen (entre lente y cristalino) se puede aplicar la relación entre foco
| \displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} } |
Si en este caso el foco es
| \displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i } |
donde
ID:(3353, 0)
Ecuación del foco del lente cristalino
Ecuación
Si observamos la sección imagen (entre lente y cristalino) - cristalino - imagen sobre la retina, se puede aplicar la relación entre foco
| \displaystyle\frac{1}{ f_{lc} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_{lc} } |
En este caso no disponemos de la distancia entre imagen entre lente y cristalino y cristalino. Sin embargo se se define la la distancia entre lente y cristalino como
| \displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b } |
donde
ID:(3354, 0)
Ecuación distancia lente optico cristalino
Ecuación
De la ecuación para el foco del lente óptico
| \displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i } |
y la del cristalino
| \displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b } |
la distancia entre lente y cristalino
| \displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c } |
Como es
| \displaystyle\frac{1}{ f_{lv} }=\displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ s_i } |
\\n\\nse tiene que\\n\\n
s_i = \displaystyle\frac{1}{\displaystyle\frac{1}{ f_l } - \displaystyle\frac{1}{ s_o }}
con lo que
| \displaystyle\frac{1}{ f_c }=\displaystyle\frac{1}{ D - s_i }+ \displaystyle\frac{1}{ s_b } |
se obtiene
| \displaystyle\frac{1}{ s_o }+\displaystyle\frac{1}{ D -\displaystyle\frac{1}{\displaystyle\frac{1}{ f_{lv} }-\displaystyle\frac{1}{ s_b }}}=\displaystyle\frac{1}{ f_c } |
donde
ID:(3355, 0)